
Concept explainers
A quantitative measure of how efficiently spheres pack into unit cells is called packing efficiency, which is the percentage of the cell space occupied by the spheres. Calculate the packing efficiencies of a simple cubic cell, a body-centered cubic cell, and a face-centered cubic cell. (Hint: Refer to Figure 11.22 and use the relationship that the volume of a sphere is
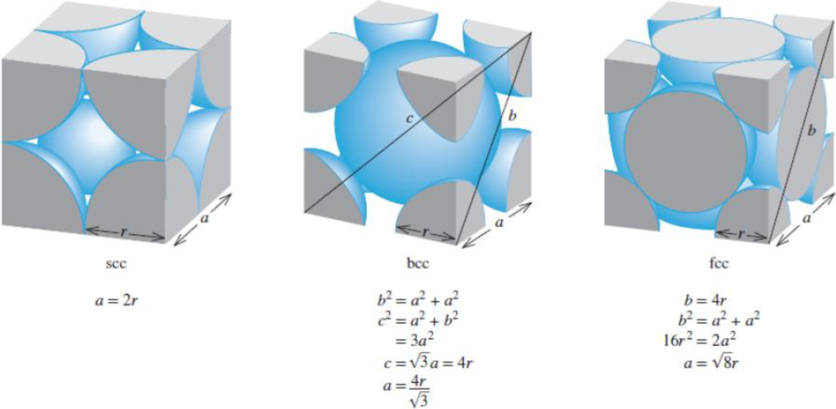
Figure 11.22 The relationship between the edge length (a) and radius (r) of atoms in the simple cubic cell, body-centered cubic cell, and face-centered cubic cell.
Interpretation: Packing efficiency of a simple cubic cell, body-centred cubic and face-centred cubic unit cells, have to be calculated.
Concept Introduction:
The major types of cubic unit cells are:
- Simple cubic unit cell.
- Face-centered cubic unit cell.
- Body-centered cubic unit cell.
Packing efficiency, is the percentage of the cell space occupied by the spheres in a cubic unit cell of any type. The atoms in the unit cells are considered as spheres.
Answer to Problem 11.134QP
The packing efficiency of a simple cubic unit cell is
The packing efficiency of a body-centred cubic unit cell is
The packing efficiency of a face-centered cubic unit cell is
Explanation of Solution
Calculating the packing efficiency for a simple cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the simple cubic unit cell is 1.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the simple cubic unit cell can be expressed as:
Thus, the packing efficiency of a simple cubic unit cell is
Calculating the packing efficiency for a body-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 2.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a body-centered cubic unit cell is
Calculating the packing efficiency for a face-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 4.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a face-centered cubic unit cell is
Using figure 11.2 as reference, the packing efficiency for the different types of cubic unit cells have been calculated.
Want to see more full solutions like this?
Chapter 11 Solutions
Chemistry
- What is the final product when hexanedioic acid reacts with 1º PCl5 and 2º NH3.arrow_forwardWhat is the final product when D-galactose reacts with hydroxylamine?arrow_forwardIndicate the formula of the product obtained by reacting methyl 5-chloro-5-oxopentanoate with 1 mole of 4-penten-1-ylmagnesium bromide.arrow_forward
- The temperature on a sample of pure X held at 1.25 atm and -54. °C is increased until the sample boils. The temperature is then held constant and the pressure is decreased by 0.42 atm. On the phase diagram below draw a path that shows this set of changes. pressure (atm) 2 0 0 200 400 temperature (K) Xarrow_forwardQUESTION: Answer Question 5: 'Calculating standard error of regression' STEP 1 by filling in all the empty green boxes *The values are all provided in the photo attached*arrow_forwardpressure (atm) 3 The pressure on a sample of pure X held at 47. °C and 0.88 atm is increased until the sample condenses. The pressure is then held constant and the temperature is decreased by 82. °C. On the phase diagram below draw a path that shows this set of changes. 0 0 200 temperature (K) 400 аarrow_forward
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning





