Chapter 11, Problem 11.37QP

What is the coordination number of each sphere in (a) a simple cubic cell, (b) a body-centered cubic cell, and (c) a face-centered cubic cell? Assume the spheres are all the same.

Interpretation Introduction

Interpretation:

The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.

Concept Introduction:

The simplest and basic unit of a crystalline solid is known as unit cell.  It is cubic in shape.  It is the building block of crystalline solids.  The unit cells repeat themselves to build a lattice.  Crystalline solids consist of many of such lattices.  There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.

In packing of the components in a solid, the components are imagined as spheres.  A simple cubic unit cell is the simplest form of a cubic unit cell.  A cube has eight vertices, twelve edges and six faces.  Similarly a cubic unit cell has eight vertices, twelve edges and six faces.  If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has $\frac{\text{1}}{\text{8}}\text{th}$ of an atom at each vertex.  Thus the number of atoms per simple cubic unit cell is –

$\text{8 }\text{vertices}\text{× }\frac{\text{1}}{\text{8}}\text{th}\text{of an }\text{atom}\text{=}\text{1}\text{atom}$

In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex.  Further one atom occupies the center of the cube.  Thus the number of atoms per unit cell in BCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms }\text{in}\text{corners}\text{+}\text{1}\text{atom}\text{at}\text{the}\text{center}\text{=}\text{1}\text{+}\text{1}\text{=}\text{2}\text{atoms}$

In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face.  Thus the number of atoms per unit cell in FCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms}\text{ in}\text{corners}\text{+}\text{6}\text{×}\frac{\text{1}}{\text{2}}\text{atoms}\text{ in}\text{faces}\text{=}\text{1}\text{+}\text{3}\text{=}\text{4}\text{atoms}$

Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.

Answer to Problem 11.37QP

Co-ordination number of simple cubic unit cell is six.

Explanation of Solution

In simple cubic unit cell each sphere at the corner of the cubic unit cell is shared by eight other spheres.  Each sphere is surrounded by six spheres.

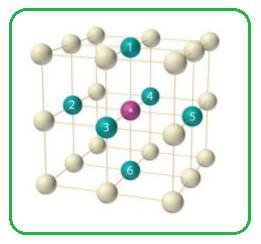
Figure 1

Thus the co-ordination number of simple cubic unit cell is six.

Interpretation Introduction

Interpretation:

The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.

Concept Introduction:

The simplest and basic unit of a crystalline solid is known as unit cell.  It is cubic in shape.  It is the building block of crystalline solids.  The unit cells repeat themselves to build a lattice.  Crystalline solids consist of many of such lattices.  There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.

In packing of the components in a solid, the components are imagined as spheres.  A simple cubic unit cell is the simplest form of a cubic unit cell.  A cube has eight vertices, twelve edges and six faces.  Similarly a cubic unit cell has eight vertices, twelve edges and six faces.  If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has $\frac{\text{1}}{\text{8}}\text{th}$ of an atom at each vertex.  Thus the number of atoms per simple cubic unit cell is –

$\text{8 }\text{vertices}\text{× }\frac{\text{1}}{\text{8}}\text{th}\text{of an }\text{atom}\text{=}\text{1}\text{atom}$

In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex.  Further one atom occupies the center of the cube.  Thus the number of atoms per unit cell in BCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms }\text{in}\text{corners}\text{+}\text{1}\text{atom}\text{at}\text{the}\text{center}\text{=}\text{1}\text{+}\text{1}\text{=}\text{2}\text{atoms}$

In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face.  Thus the number of atoms per unit cell in FCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms}\text{ in}\text{corners}\text{+}\text{6}\text{×}\frac{\text{1}}{\text{2}}\text{atoms}\text{ in}\text{faces}\text{=}\text{1}\text{+}\text{3}\text{=}\text{4}\text{atoms}$

Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.

Answer to Problem 11.37QP

Co-ordination number of Body-centered cubic unit cell is eight.

Explanation of Solution

There are two spheres per BCC unit cell.  Each sphere touches eight other spheres.

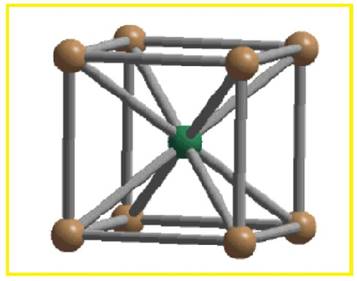
Figure 2

Thus the co-ordination number of body-centered cubic unit cell is eight.

Interpretation Introduction

Interpretation:

The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.

Concept Introduction:

The simplest and basic unit of a crystalline solid is known as unit cell.  It is cubic in shape.  It is the building block of crystalline solids.  The unit cells repeat themselves to build a lattice.  Crystalline solids consist of many of such lattices.  There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.

In packing of the components in a solid, the components are imagined as spheres.  A simple cubic unit cell is the simplest form of a cubic unit cell.  A cube has eight vertices, twelve edges and six faces.  Similarly a cubic unit cell has eight vertices, twelve edges and six faces.  If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has $\frac{\text{1}}{\text{8}}\text{th}$ of an atom at each vertex.  Thus the number of atoms per simple cubic unit cell is –

$\text{8 }\text{vertices}\text{× }\frac{\text{1}}{\text{8}}\text{th}\text{of an }\text{atom}\text{=}\text{1}\text{atom}$

In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex.  Further one atom occupies the center of the cube.  Thus the number of atoms per unit cell in BCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms }\text{in}\text{corners}\text{+}\text{1}\text{atom}\text{at}\text{the}\text{center}\text{=}\text{1}\text{+}\text{1}\text{=}\text{2}\text{atoms}$

In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face.  Thus the number of atoms per unit cell in FCC unit cell is,

$\text{8}\text{×}\frac{\text{1}}{\text{8}}\text{atoms}\text{ in}\text{corners}\text{+}\text{6}\text{×}\frac{\text{1}}{\text{2}}\text{atoms}\text{ in}\text{faces}\text{=}\text{1}\text{+}\text{3}\text{=}\text{4}\text{atoms}$

Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.

Answer to Problem 11.37QP

Co-ordination number of Face-centered cubic unit cell is twelve.

Explanation of Solution

There are four spheres per FCC unit cell. Each sphere is in contact with twelve spheres.

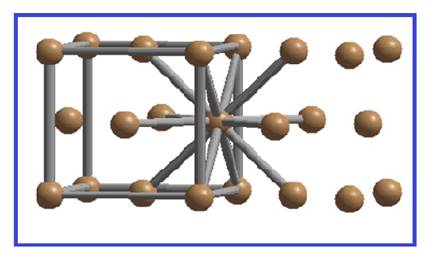
Figure 3

Thus the co-ordination number of simple cubic unit cell is twelve.