
The cantilevered beam has a circular cross section. If it supports a force P at its end, determine its radius y as a function of x so that it is subjected to a constant maximum bending stress σallow throughout its length.
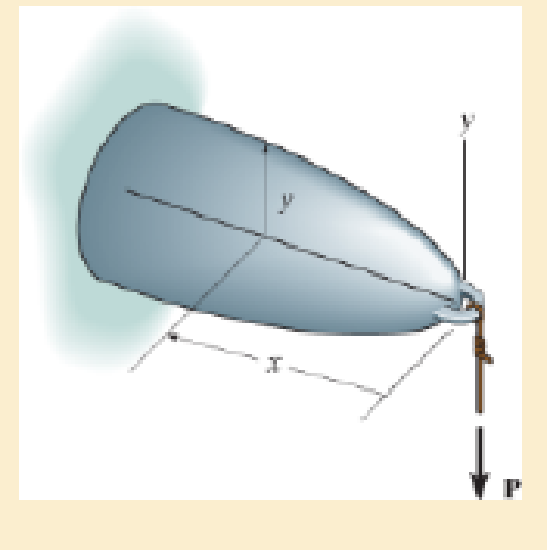
The radius y as a function of x.
Answer to Problem 11.1RP
The radius y as a function of x is
Explanation of Solution
Given information:
The force is P.
Calculation:
Sketch the free body diagram of cantilever beam as shown in Figure 1:
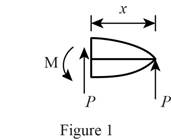
Let, M is the moment acting cantilever beam and V is the shear force.
Consider the length is x.
Refer to Figure 1:
Calculate the shear force as follows:
Calculate the moment as shown below:
Sketch the calculated values as shown in Figure 2.
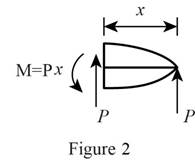
Write the section properties as follows:
Calculate the moment of inertia (I) as shown in below:
Here, c is the radius of section.
Substitute y for c in Equation (1).
Find the value of section modulus S as shown in below:
Here, I is the moment of inertia and c is the centroid of section.
Substitute
Calculate the allowable bending stress
Here, M is the moment.
Substitute
Hence, the radius y as a function of x is
Want to see more full solutions like this?
Chapter 11 Solutions
Mechanics of Materials (10th Edition)
Additional Engineering Textbook Solutions
Fluid Mechanics: Fundamentals and Applications
Thermodynamics: An Engineering Approach
Modern Database Management
Starting Out with C++ from Control Structures to Objects (9th Edition)
Management Information Systems: Managing The Digital Firm (16th Edition)
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
- This is a tilt and rotation question. Here are notes attached for reference. I prefer handwritten solutions. ONLY UPLOAD A SOLUTION IF YOU ARE SURE ABOUT THE ANSWER PLEASE. I prefer handwritten solutions.arrow_forwardHomework#7arrow_forwardHomework#7arrow_forwardQ3. Consider an inlet flow for an engine with a supersonic inlet Mach number as shown in Figure. below, calculate the total pressure loss between point 1 and 3 if the flow passes first an oblique shock wave and then a reflected shock wave. (30 pts) Моо M∞ = 2.0 && = 30°arrow_forwardJust do Questions 7, 9, 11. Here are notes attached for reference. I prefer handwritten solutions. ONLY UPLOAD A SOLUTION IF YOU ARE SURE ABOUT THE ANSWER PLEASE. (If you have once answered this question don't answer it again)arrow_forwardThis is a tilt and rotation question. Here are notes attached for reference. I prefer handwritten solutions. ONLY UPLOAD A SOLUTION IF YOU ARE SURE ABOUT THE ANSWER PLEASE. I prefer handwritten solutions.arrow_forwardPlease explain each steparrow_forwardJust do Questions 7, 9, 11. Here are notes attached for reference. I prefer handwritten solutions. ONLY UPLOAD A SOLUTION IF YOU ARE SURE ABOUT THE ANSWER PLEASE.arrow_forwardExample Consider the simplified model of an automobile shown in Figure, let the parameter have the values m = 1500 kg, Ic = 2000 kg m2, k₁ = 36000 kg/m, k₁ = 40000 kg/m, a = 1.3 m and b = 1.7 m, calculate the natural modes of the system and write the expression for the response. ט 0 Solution T Equilibrium position 6(1)arrow_forward6.3 Contamination of vegetable oil Vegetable oil is used in a food processing factory to prepare instant breadcrumbs. A stirred tank is used to hold the oil. During operation of the breadcrumb process, oil is pumped from the tank at a rate of 4.8 1 h-¹. At 8 PM during the night shift, the tank is mistakenly connected to a drum of cod liver oil, which is then pumped into the tank. The volume of vegetable oil in the tank at 8 PM is 60 1. (a) If the flow rate of cod liver oil into the tank is 7.5 1h-1 and the tank has a maximum capacity of 100 1, will the tank overflow before the factory manager arrives at 9 AM? Assume that the density of both oils is the same. (b) If cod liver oil is pumped into the tank at a rate of 4.8 1 h 1 instead of 7.5 1 h−1, what is the composition of oil in the tank at midnight?arrow_forward6.1 Dilution of sewage In a sewage treatment plant, a large concrete tank initially contains 440,000 litres of liquid and 10,000 kg of fine suspended solids. To flush this material out of the tank, water is pumped into the vessel at a rate of 40,000 1 h −1. Liquid containing solids leaves at the same rate. Estimate the concentration of suspended solids in the tank at the end of 5 h. State your assumptions.arrow_forward6.13 Heating glycerol solution An adiabatic stirred tank is used to heat 100 kg of a 45% glycerol solution in water. An electrical coil delivers 2.5 kW of power to the tank; 88% of the energy delivered by the coil goes into heating the vessel contents. The glycerol solution is initially at 15°C. (a) Write a differential equation for the energy balance. (b) Integrate the equation to obtain an expression for temperature as a function of time. (c) Assuming glycerol and water form an ideal solution, how long will the solution take to reach 90°C?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY