Chapter 10.7, Problem 51AYU

Catching a Train Bill’s train leaves at 8:06 AM and accelerates at the rate of 2 meters per second per second. Bill, who can run 5 meters per second, arrives at the train station 5 seconds after the train has left and runs for the train.

a. Find parametric equations that model the motions of the train and Bill as a function of time.

[Hint: The position s at time $t$ of an object having acceleration $a$ is $s=\frac{1}{2}a{t}^2$].

b. Determine algebraically whether Bill will catch the train. If so, when?

c. Simulate the motion of the train and Bill by simultaneously graphing the equations found in part (a).

To determine

To find:

a. Parametric equations that model the motions of the train and Bill as a function of time. [Hint: The position s at time $t$ of an object having acceleration as is $s=1/2at²$].

Answer to Problem 51AYU

a. Train: $\left(t^2, 1\right)$, Bill’s: $\left(5\left(t - 5\right), 5\right)$.

Explanation of Solution

Given:

Bill’s train leaves at 8:06 am and accelerates at the rate of 2 meters per second per second. Bill, who can run 5 meters per second, arrives at the train station 5 seconds after the train has left and runs for the train.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be train’s path; $y_2 = 5$ be bill’s path.

a. Train: $x_1 = \frac{1}{2}\left(2\right)t² = t²$

$y_1 = 1$

Bill:

$x_2 = 5\left(t - 5\right)$

$y_2 = 5$

To determine

To find:

b. Algebraically whether Bill will catch the train. If so, when?

Answer to Problem 51AYU

b. No, He cannot catch the train.

Explanation of Solution

Given:

Bill’s train leaves at 8:06 am and accelerates at the rate of 2 meters per second per second. Bill, who can run 5 meters per second, arrives at the train station 5 seconds after the train has left and runs for the train.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be train’s path; $y_2 = 5$ be bill’s path.

b.Bill will catch the train only when $x_1 = x_2$

$t² = 5\left(t - 5\right)$

$t² - 5t + 25 = 0$

$t$ does not have any real function as $b² - 4ac = 25 - 4 \&*\#x00A0;1 \&*\#x00A0;25 = -75 < 0$

Hence Bill cannot catch the train.

To determine

To find:

c. Simulate the motion of the train and Bill by simultaneously graphing the equations found in part (a).

Answer to Problem 51AYU

c.

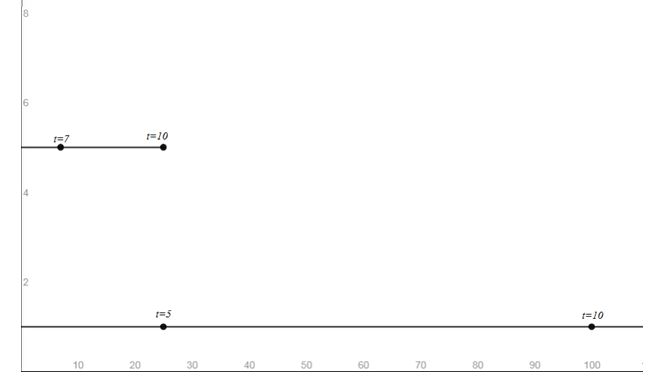
Explanation of Solution

Given:

Bill’s train leaves at 8:06 am and accelerates at the rate of 2 meters per second per second. Bill, who can run 5 meters per second, arrives at the train station 5 seconds after the train has left and runs for the train.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be train’s path; $y_2 = 5$ be bill’s path.

c.