
Precalculus
9th Edition
ISBN: 9780321716835
Author: Michael Sullivan
Publisher: Addison Wesley
expand_more
expand_more
format_list_bulleted
Question
Chapter 10.4, Problem 69AYU
To determine
To find: Analyze the equation.
Expert Solution & Answer
Answer to Problem 69AYU
The equation represents parabola.
Explanation of Solution
Given:
Formula used:
| Vertex | Focus | Directrix | Equation | Description |
| Parabola, axis of symmetry is parallel to , opens up |
Calculation:
Given that .
The equation represents parabola.
The axis of symmetry is parallel to .
Vertex: .
Hence, .
,
Focus: .
The coordinates of the focus is .
Directrix: .
The graph of the equation of is plotted.
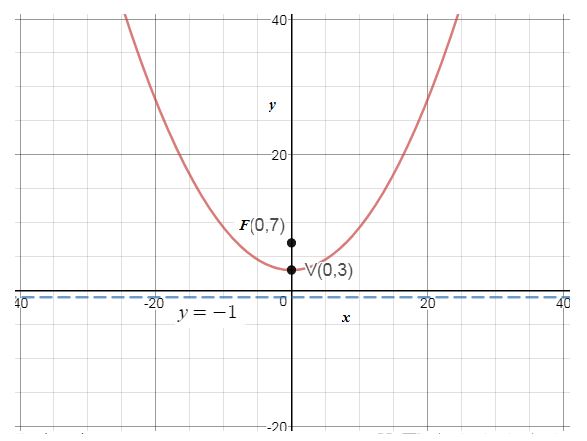
Using the given equation , we plot the graph using graphing tool.
The graph represents a parabola, with vertex , directrix and the axis of symmetry is , opens up.
Chapter 10 Solutions
Precalculus
Ch. 10.2 - The formula for the distance d from P 1 =( x 1 , y...Ch. 10.2 - To complete the square of x 2 4x , add_______...Ch. 10.2 - Use the Square Root Method to find the real...Ch. 10.2 - The point that is symmetric with respect to the...Ch. 10.2 - To graph y= ( x3 ) 2 +1 , shift the graph of y= x...Ch. 10.2 - _________ is the collection of all points in a...Ch. 10.2 - Prob. 7AYUCh. 10.2 - Prob. 8AYUCh. 10.2 - Prob. 9AYUCh. 10.2 - Prob. 10AYU
Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 13-20, the graph of a parabola is...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems 21-38, find the equation of the...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 3956, find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 3956, find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 3956, find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 3956, find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 3956, find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems , find the vertex, focus, and...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - In Problems 57-64, write an equation for each...Ch. 10.2 - Satellite Dish A satellite dish is shaped like a...Ch. 10.2 - Prob. 64AYUCh. 10.2 - Prob. 65AYUCh. 10.2 - Prob. 66AYUCh. 10.2 - Prob. 67AYUCh. 10.2 - Prob. 68AYUCh. 10.2 - Prob. 69AYUCh. 10.2 - Prob. 70AYUCh. 10.2 - Prob. 71AYUCh. 10.2 - Prob. 72AYUCh. 10.2 - Prob. 73AYUCh. 10.2 - Prob. 74AYUCh. 10.2 - Prob. 75AYUCh. 10.2 - Prob. 76AYUCh. 10.2 - Prob. 77AYUCh. 10.2 - Prob. 78AYUCh. 10.2 - Prob. 79AYUCh. 10.3 - The distance d from P 1 =( 2,5 ) to P 2 =( 4,2 )...Ch. 10.3 - To complete the square of x 2 3x , Add _____. (p....Ch. 10.3 - Find the intercepts of the equation y 2 =164 x 2 ....Ch. 10.3 - The point that is symmetric with respect to the...Ch. 10.3 - The point that is symmetric with respect to the...Ch. 10.3 - Prob. 6AYUCh. 10.3 - A(n) _______ is the collection of all points in a...Ch. 10.3 - Multiple Choice For an ellipse, the foci lie on a...Ch. 10.3 - For the ellipse x 2 4 + y 2 25 =1 , the vertices...Ch. 10.3 - For the ellipse x 2 25 + y 2 9 =1 , the value of a...Ch. 10.3 - If the center of an ellipse is ( 2,3 ) , the major...Ch. 10.3 - Prob. 12AYUCh. 10.3 - In problems 13-16, the graph of an ellipse is...Ch. 10.3 - In problems 13-16, the graph of an ellipse is...Ch. 10.3 - In problems 13-16, the graph of an ellipse is...Ch. 10.3 - In problems 13-16, the graph of an ellipse is...Ch. 10.3 - In Problems 1726, analyze each equation. That is,...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems 1726, analyze each equation. That is,...Ch. 10.3 - In Problems 1726, analyze each equation. That is,...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems analyze each equation. That is, find...Ch. 10.3 - In Problems 1726, analyze each equation. That is,...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 27-38, find an equation for each...Ch. 10.3 - In Problems 39-42, write an equation for each...Ch. 10.3 - In Problems 39-42, write an equation for each...Ch. 10.3 - In Problems 39-42, write an equation for each...Ch. 10.3 - In Problems 39-42, write an equation for each...Ch. 10.3 - In Problems analyze each equationthat is, find...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems analyze each equationthat is, find...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems analyze each equationthat is, find...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems analyze each equationthat is, find...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems 4354, analyze each equation ; that is,...Ch. 10.3 - In Problems analyze each equationthat is, find...Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems , find an equation for each ellipse....Ch. 10.3 - In Problems , find an equation for each ellipse....Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems , find an equation for each ellipse....Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems 5564, find an equation for each...Ch. 10.3 - In Problems , find an equation for each ellipse....Ch. 10.3 - In Problems 65-68, graph each function. Be sure to...Ch. 10.3 - In Problems 65-68, graph each function. Be sure to...Ch. 10.3 - In Problems 65-68, graph each function. Be sure to...Ch. 10.3 - In Problems 65-68, graph each function. Be sure to...Ch. 10.3 - Semielliptical Arch Bridge An arch in the shape of...Ch. 10.3 - Semielliptical Arch Bridge The arch of a bridge is...Ch. 10.3 - Whispering Gallery A hall 100 feet in length is to...Ch. 10.3 - Whispering Gallery Jim, standing at one focus of a...Ch. 10.3 - Semielliptical Arch Bridge A bridge is built in...Ch. 10.3 - Semielliptical Arch Bridge A bridge is to be built...Ch. 10.3 - Racetrack Design Consult the figure. A racetrack...Ch. 10.3 - Semielliptical Arch Bridge An arch for a bridge...Ch. 10.3 - Installing a Vent Pipe A homeowner is putting in a...Ch. 10.3 - Semielliptical Arch Bridge An arch for a bridge...Ch. 10.3 - In Problems 79-83, use the fact that the orbit of...Ch. 10.3 - In Problems 79-83, use the fact that the orbit of...Ch. 10.3 - In Problems 79-83, use the fact that the orbit of...Ch. 10.3 - In Problems 79-83, use the fact that the orbit of...Ch. 10.3 - Prob. 83AYUCh. 10.3 - Prob. 84AYUCh. 10.3 - Prob. 85AYUCh. 10.4 - The distance d from P 1 =( 2,5 ) to P 2 =( 4,2 )...Ch. 10.4 - Prob. 2AYUCh. 10.4 - Prob. 3AYUCh. 10.4 - Prob. 4AYUCh. 10.4 - Prob. 5AYUCh. 10.4 - Prob. 6AYUCh. 10.4 - A(n) _______ is the collection of points in a...Ch. 10.4 - For a hyperbola, the foci lie on a line called the...Ch. 10.4 - Answer Problems 9-11 using the figure to the...Ch. 10.4 - Answer Problems 9-11 using the figure to the...Ch. 10.4 - Answer Problems 9-11 using the figure to the...Ch. 10.4 - In a hyperbola, if a=3 and c=5 , then b= ________....Ch. 10.4 - For the hyperbola x 2 4 y 2 9 =1 , the value of a...Ch. 10.4 - For the hyperbola y 2 16 x 2 81 =1 , the...Ch. 10.4 - In Problems 15-18, the graph of a hyperbola is...Ch. 10.4 - In Problems 15-18, the graph of a hyperbola is...Ch. 10.4 - In Problems 15-18, the graph of a hyperbola is...Ch. 10.4 - In Problems 15-18, the graph of a hyperbola is...Ch. 10.4 - In Problems 1928, find an equation for the...Ch. 10.4 - In Problems 1928, find an equation for the...Ch. 10.4 - In Problems, find an equation for the hyperbola...Ch. 10.4 - In Problems, find an equation for the hyperbola...Ch. 10.4 - In Problems, find an equation for the hyperbola...Ch. 10.4 - In Problems, find an equation for the hyperbola...Ch. 10.4 - In Problems, find an equation for the hyperbola...Ch. 10.4 - In Problems 1928, find an equation for the...Ch. 10.4 - In Problems 1928, find an equation for the...Ch. 10.4 - In Problems 1928, find an equation for the...Ch. 10.4 - In Problems, find the center , transverse axis,...Ch. 10.4 - In Problems, find the center , transverse axis,...Ch. 10.4 - In Problems 2936, find the center, transverse...Ch. 10.4 - In Problems 2936, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems 2936, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems 2936, find the center, transverse...Ch. 10.4 - In Problems 37-40, write an equation for each...Ch. 10.4 - In Problems 37-40, write an equation for each...Ch. 10.4 - In Problems 37-40, write an equation for each...Ch. 10.4 - In Problems 37-40, write an equation for each...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 41-48, find an equation for the...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems 4962, find the center, transverse...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - In Problems, find the center, transverse axis,...Ch. 10.4 - Prob. 63AYUCh. 10.4 - Prob. 64AYUCh. 10.4 - Prob. 65AYUCh. 10.4 - Prob. 66AYUCh. 10.4 - Prob. 67AYUCh. 10.4 - Prob. 68AYUCh. 10.4 - Prob. 69AYUCh. 10.4 - Prob. 70AYUCh. 10.4 - Prob. 71AYUCh. 10.4 - Prob. 72AYUCh. 10.4 - Prob. 73AYUCh. 10.4 - Prob. 74AYUCh. 10.4 - Fireworks Display Suppose that two people standing...Ch. 10.4 - Lightning Strikes Suppose that two people standing...Ch. 10.4 - Nuclear Power Plaut Some nuclear power plants...Ch. 10.4 - Prob. 78AYUCh. 10.4 - Rutherford’s Experiment In May 1911, Ernest...Ch. 10.4 - Prob. 80AYUCh. 10.4 - Prob. 81AYUCh. 10.4 - Prob. 82AYUCh. 10.4 - Prob. 83AYUCh. 10.4 - Prob. 84AYUCh. 10.4 - Prob. 85AYUCh. 10.4 - Prob. 86AYUCh. 10.5 - The sum formula for the sine function is sin( A+B...Ch. 10.5 - The Double-angle Formula for the sine function is...Ch. 10.5 - If is acute, the Half-angle Formula for the sine...Ch. 10.5 - If is acute, the Half-angle Formula for the...Ch. 10.5 - To transform the equation A x 2 +Bxy+C y 2...Ch. 10.5 - Except for degenerate cases, the equation A x 2...Ch. 10.5 - Except for degenerate cases, the equation A x 2...Ch. 10.5 - Prob. 8AYUCh. 10.5 - Prob. 9AYUCh. 10.5 - Prob. 10AYUCh. 10.5 - Prob. 11AYUCh. 10.5 - Prob. 12AYUCh. 10.5 - Prob. 13AYUCh. 10.5 - Prob. 14AYUCh. 10.5 - Prob. 15AYUCh. 10.5 - Prob. 16AYUCh. 10.5 - Prob. 17AYUCh. 10.5 - Prob. 18AYUCh. 10.5 - Prob. 19AYUCh. 10.5 - Prob. 20AYUCh. 10.5 - Prob. 21AYUCh. 10.5 - Prob. 22AYUCh. 10.5 - Prob. 23AYUCh. 10.5 - Prob. 24AYUCh. 10.5 - Prob. 25AYUCh. 10.5 - Prob. 26AYUCh. 10.5 - Prob. 27AYUCh. 10.5 - Prob. 28AYUCh. 10.5 - Prob. 29AYUCh. 10.5 - Prob. 30AYUCh. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - Prob. 35AYUCh. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - In Problems 31-42, rotate the axes so that the new...Ch. 10.5 - Prob. 43AYUCh. 10.5 - Prob. 44AYUCh. 10.5 - Prob. 45AYUCh. 10.5 - Prob. 46AYUCh. 10.5 - Prob. 47AYUCh. 10.5 - Prob. 48AYUCh. 10.5 - Prob. 49AYUCh. 10.5 - Prob. 50AYUCh. 10.5 - Prob. 51AYUCh. 10.5 - Prob. 52AYUCh. 10.5 - Prob. 53AYUCh. 10.5 - Prob. 54AYUCh. 10.5 - Prob. 55AYUCh. 10.5 - Prob. 56AYUCh. 10.5 - Prob. 57AYUCh. 10.5 - Prob. 58AYUCh. 10.5 - Prob. 59AYUCh. 10.5 - Prob. 60AYUCh. 10.6 - Prob. 1AYUCh. 10.6 - Prob. 2AYUCh. 10.6 - Prob. 3AYUCh. 10.6 - Prob. 4AYUCh. 10.6 - Prob. 5AYUCh. 10.6 - Prob. 6AYUCh. 10.6 - Prob. 7AYUCh. 10.6 - Prob. 8AYUCh. 10.6 - Prob. 9AYUCh. 10.6 - Prob. 10AYUCh. 10.6 - Prob. 11AYUCh. 10.6 - Prob. 12AYUCh. 10.6 - In Problems 13-24, analyze each equation and graph...Ch. 10.6 - In Problems 13-24, analyze each equation and graph...Ch. 10.6 - In Problems 13-24, analyze each equation and graph...Ch. 10.6 - Prob. 16AYUCh. 10.6 - Prob. 17AYUCh. 10.6 - Prob. 18AYUCh. 10.6 - Prob. 19AYUCh. 10.6 - In Problems 13-24, analyze each equation and graph...Ch. 10.6 - Prob. 21AYUCh. 10.6 - Prob. 22AYUCh. 10.6 - Prob. 23AYUCh. 10.6 - Prob. 24AYUCh. 10.6 - Prob. 25AYUCh. 10.6 - Prob. 26AYUCh. 10.6 - Prob. 27AYUCh. 10.6 - Prob. 28AYUCh. 10.6 - Prob. 29AYUCh. 10.6 - Prob. 30AYUCh. 10.6 - Prob. 31AYUCh. 10.6 - Prob. 32AYUCh. 10.6 - Prob. 33AYUCh. 10.6 - Prob. 34AYUCh. 10.6 - Prob. 35AYUCh. 10.6 - Prob. 36AYUCh. 10.6 - Prob. 37AYUCh. 10.6 - Prob. 38AYUCh. 10.6 - Prob. 39AYUCh. 10.6 - Prob. 40AYUCh. 10.6 - Prob. 41AYUCh. 10.6 - Prob. 42AYUCh. 10.6 - Prob. 43AYUCh. 10.6 - Prob. 44AYUCh. 10.6 - Prob. 45AYUCh. 10.6 - Prob. 46AYUCh. 10.7 - The function f( x )=3sin( 4x ) has amplitude...Ch. 10.7 - Prob. 2AYUCh. 10.7 - Prob. 3AYUCh. 10.7 - Prob. 4AYUCh. 10.7 - Prob. 5AYUCh. 10.7 - Prob. 6AYUCh. 10.7 - In Problems graph the plane curve whose parametric...Ch. 10.7 - Prob. 8AYUCh. 10.7 - Prob. 9AYUCh. 10.7 - Prob. 10AYUCh. 10.7 - Prob. 11AYUCh. 10.7 - Prob. 12AYUCh. 10.7 - Prob. 13AYUCh. 10.7 - Prob. 14AYUCh. 10.7 - Prob. 15AYUCh. 10.7 - Prob. 16AYUCh. 10.7 - Prob. 17AYUCh. 10.7 - Prob. 18AYUCh. 10.7 - In Problems 726, graph the plane curve whose...Ch. 10.7 - Prob. 20AYUCh. 10.7 - Prob. 21AYUCh. 10.7 - In Problems graph the plane curve whose parametric...Ch. 10.7 - In Problems graph the plane curve whose parametric...Ch. 10.7 - Prob. 24AYUCh. 10.7 - Prob. 25AYUCh. 10.7 - Prob. 26AYUCh. 10.7 - Prob. 27AYUCh. 10.7 - Prob. 28AYUCh. 10.7 - Prob. 29AYUCh. 10.7 - Prob. 30AYUCh. 10.7 - Prob. 31AYUCh. 10.7 - Prob. 32AYUCh. 10.7 - Prob. 33AYUCh. 10.7 - Prob. 34AYUCh. 10.7 - Prob. 35AYUCh. 10.7 - Prob. 36AYUCh. 10.7 - Prob. 37AYUCh. 10.7 - Prob. 38AYUCh. 10.7 - Prob. 39AYUCh. 10.7 - In Problems 39-42, find parametric equations for...Ch. 10.7 - Prob. 41AYUCh. 10.7 - Prob. 42AYUCh. 10.7 - Prob. 43AYUCh. 10.7 - Prob. 44AYUCh. 10.7 - In Problems 45-48, use a graphing utility to graph...Ch. 10.7 - Prob. 46AYUCh. 10.7 - Prob. 47AYUCh. 10.7 - Prob. 48AYUCh. 10.7 - Prob. 49AYUCh. 10.7 - Prob. 50AYUCh. 10.7 - Catching a Train Bill’s train leaves at 8:06 AM...Ch. 10.7 - Prob. 52AYUCh. 10.7 - Prob. 53AYUCh. 10.7 - Prob. 54AYUCh. 10.7 - Prob. 55AYUCh. 10.7 - Prob. 56AYUCh. 10.7 - Prob. 57AYUCh. 10.7 - Uniform Motion A Cessna (heading south at mph)...Ch. 10.7 - The Green Monster The left field wall at Fenway...Ch. 10.7 - Prob. 60AYUCh. 10.7 - Prob. 61AYUCh. 10.7 - Prob. 62AYUCh. 10.7 - Prob. 63AYUCh. 10.7 - Prob. 64AYUCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - In Problems 13, identify each equation. If it is a...Ch. 10 - In Problems 13, identify each equation. If it is a...Ch. 10 - In Problems identify each equation. If it is a...Ch. 10 - In Problems 46, find an equation of the conic...Ch. 10 - In Problems find an equation of the conic...Ch. 10 - In Problems find an equation of the conic...Ch. 10 - In Problems 79, identify each conic without...Ch. 10 - In Problems 79, identify each conic without...Ch. 10 - In Problems identify each conic without completing...Ch. 10 - Prob. 10CTCh. 10 - Prob. 11CTCh. 10 - Prob. 12CTCh. 10 - A parabolic reflector (paraboloid of revolution)...Ch. 10 - For find
Ch. 10 - In the complex number system, solve the equation
...Ch. 10 - For what numbers x is 6xx2 ?Ch. 10 - Prob. 4CRCh. 10 - Prob. 5CRCh. 10 - Prob. 6CRCh. 10 - Prob. 7CRCh. 10 - Prob. 8CRCh. 10 - Prob. 9CRCh. 10 - Prob. 10CRCh. 10 - Solve the equation where.
Ch. 10 - Find the rectangle equation of the plane curve...
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 1–8, use the Ratio Test to determine whether each series converges absolutely or diverges.
1.
University Calculus: Early Transcendentals (4th Edition)
Derivatives of inverse sine Evaluate the derivatives of the following functions. 10. f(x) = sin1 (ln x)
Calculus: Early Transcendentals (2nd Edition)
the ratio as a fraction.
Pre-Algebra Student Edition
4. Correlation and Causation What is meant by the statement that “correlation does imply causation”?
Elementary Statistics
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Knowledge Booster
Similar questions
- A 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forwardExplain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)arrow_forwarduse Integration by Parts to derive 12.6.1arrow_forward
- Explain the relationship between 12.3.6, (case A of 12.3.6) and 12.3.7arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forward
- use Corollary 12.6.2 and 12.6.3 to derive 12.6.4,12.6.5, 12.6.6 and 12.6.7arrow_forwardExplain the focus and reasons for establishment of 12.5.1(lim(n->infinite) and sigma of k=0 to n)arrow_forwardExplain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning