
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
8th Edition
ISBN: 9781259676512
Author: Kenneth H Rosen
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10.6, Problem 24E
Show that Dijkstra's algorithm may not work if edges can have negative weights.
ALGORITHM 2 Floyd's Algorithm.
procedureFloyd(G:weighted simple graph) {Ghas verticesv1,v2,...,vnand weights w(vi,vj)
withw(vi,vj)= ?? if{vt,vj}is not an edge}
fori: =1 tonfor:=1ton
d(vi,vj):= w(vi,vf)
fori: =1 tonfor j:= 1tonfork: = 1tonifd(vi,vj)+d(vi,vk)
thend(vj,vk):=d(vj,vi)+d(vi,vk)returnd(vi,vj){d(vi,vj)isthelength of a shortest path between viand vjfor 1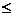 i
i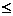 n,1
n,1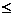 j
j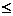 n}
n}
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
PLEASE SOLVE STEP BY STEP WITHOUT ARTIFICIAL INTELLIGENCE OR CHATGPT
SOLVE BY HAND STEP BY STEP
4.- A beer at an unknown temperature is introduced into a refrigerator that has a constant temperature of 1°C. After 20 minutes, the temperature of the beer is 10°C, and after 40 minutes, the temperature of the beer is 6°C.
a) Determine the temperature at which the beer was placed inside the refrigerator.b) How long will it take for the beer to reach 2°C?
PLEASE SOLVE STEP BY STEP WITHOUT ARTIFICIAL INTELLIGENCE OR CHATGPT
SOLVE BY HAND STEP BY STEP
5.- It is known that the population of a certain community increases at a rate proportional to the number of people at any given moment. If the population doubled in 5 years:
a) How long will it take to triple?b) How long will it take to quadruple?
Use the graph to solve 3x2-3x-8=0
Chapter 10 Solutions
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
Ch. 10.1 - Draw graph models, stating the type of graph...Ch. 10.1 - Prob. 2ECh. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For each undirected graph in Exercises 3-9 that is...
Ch. 10.1 - Let G be a simple graph. Show that the relation R...Ch. 10.1 - Let G be an undirected graph with a loop at every...Ch. 10.1 - The intersection graphof a collection of...Ch. 10.1 - Use the niche overlap graph inFigure 11to...Ch. 10.1 - Construct a niche overlap graph for six species of...Ch. 10.1 - Draw the acquaintanceship graph that represents...Ch. 10.1 - Prob. 17ECh. 10.1 - Who can influence Fred and whom can Fred influence...Ch. 10.1 - Construct an influence graph for the board members...Ch. 10.1 - The word apple can refer to a plant, a food, or a...Ch. 10.1 - Prob. 21ECh. 10.1 - Which other teams did Team 4 beat and which teams...Ch. 10.1 - In a round-robin tournament the Tigers beat the...Ch. 10.1 - Construct the call graph for a set of seven...Ch. 10.1 - Explain how the two telephone call graphs for...Ch. 10.1 - a) Explain how graphs can be used to model...Ch. 10.1 - How can a graph that models e-mail messages sent...Ch. 10.1 - How can a graph that models e-mail messages sent...Ch. 10.1 - Describe a graph model that represents whether...Ch. 10.1 - Describe a graph model that represents a subway...Ch. 10.1 - Prob. 31ECh. 10.1 - Describe a graph model that represents the...Ch. 10.1 - Describe a graph model that represents traditional...Ch. 10.1 - Prob. 34ECh. 10.1 - Construct a precedence graph for the following...Ch. 10.1 - Describe a discrete structure based on a graph...Ch. 10.1 - Describe a discrete structure based on a graph...Ch. 10.1 - Prob. 38ECh. 10.2 - In Exercises 1-3 find the number of vertices, the...Ch. 10.2 - In Exercises 1-3 find the number of vertices, the...Ch. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Can a simple graph exist with 15 vertices each of...Ch. 10.2 - Show that the sum, over the set of people at a...Ch. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - For each of the graphs in Exercises 7-9 determine...Ch. 10.2 - Construct the underlying undirected graph for the...Ch. 10.2 - What does the degree of a vertex represent in the...Ch. 10.2 - Prob. 13ECh. 10.2 - What does the degree of a vertex in the Hollywood...Ch. 10.2 - What do the in-degree and the out-degree of a...Ch. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Show that in a simple graph with at least two...Ch. 10.2 - Use Exercise 18 to show that in a group of people,...Ch. 10.2 - Prob. 20ECh. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - For which values ofnare these graphs bipartite?...Ch. 10.2 - Suppose that therearefour employees in the...Ch. 10.2 - Suppose that a new company has five employees:...Ch. 10.2 - Suppose that therearefive young women and five...Ch. 10.2 - Suppose that therearefive young women and six...Ch. 10.2 - Prob. 31ECh. 10.2 - Each of Exercises 31-33 can be solved using Hall's...Ch. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Each of Exercises 31-33 can be solved using Hall's...Ch. 10.2 - Prob. 36ECh. 10.2 - How many vertices and how many edges do these...Ch. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - How many edges does a graph have if its degree...Ch. 10.2 - Prob. 43ECh. 10.2 - Determine whether each of these sequences is...Ch. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Draw all sub graphs of this graph.Ch. 10.2 - Let G be a graph with vertices and e edges. Let M...Ch. 10.2 - For which values ofnare these graphs regular? a)...Ch. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - In Exercises 58-60 find the union of the given...Ch. 10.2 - Prob. 59ECh. 10.2 - In Exercises 58-60 find the union of the given...Ch. 10.2 - The complementarygraphGof a simple graph G has the...Ch. 10.2 - IfGis a simple graph with 15 edges andGhas 13...Ch. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Describe an algorithm to decide whether a graph is...Ch. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Prob. 74ECh. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.3 - In Exercises 1-4 use an adjacency list to...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Represent the graph in Exercise 1 with an...Ch. 10.3 - Represent the graph in Exercise 2 with an...Ch. 10.3 - Represent the graph in Exercise 3 with an...Ch. 10.3 - Represent the graph in Exercise 4 with an...Ch. 10.3 - Represent each of these graphs with an adjacency...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19-21 find the adjacency matrix of...Ch. 10.3 - In Exercises 19-21 find the adjacency matrix of...Ch. 10.3 - In Exercises 22-24 draw the graph represented by...Ch. 10.3 - In Exercises 22-24 draw the graph represented by...Ch. 10.3 - In Exercises22-24 draw the graph represented by...Ch. 10.3 - Find the density of the graph in a)Figure...Ch. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Is every zero-one square matrix that is symmetric...Ch. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - What is me sum of me entries in a column of me...Ch. 10.3 - What is the sum of the entries in a row of the...Ch. 10.3 - What is the sum of the entries in a column of the...Ch. 10.3 - Find an adjacency matrix for each of these graphs....Ch. 10.3 - Prob. 37ECh. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - Show that isomorphism of simple graphs is an...Ch. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - How many non isomorphic simple graphs are there...Ch. 10.3 - How many nonisomorphic simple graphs are there...Ch. 10.3 - How many nonisomorphic simple graphs are there...Ch. 10.3 - Prob. 61ECh. 10.3 - Prob. 62ECh. 10.3 - Are the simple graphswiththe following adjacency...Ch. 10.3 - Determine whether the graphs without loops with...Ch. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - In Exercises 67-70 determine whether the given...Ch. 10.3 - Prob. 69ECh. 10.3 - In Exercises 67-70 determine whether the given...Ch. 10.3 - Show that ifGand H are isomorphic directed graphs,...Ch. 10.3 - Show that the property that a graph is bipartite...Ch. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - How much storage is needed to represent a simple...Ch. 10.3 - A devil's pairfor a purported isomorphism testis a...Ch. 10.3 - Prob. 78ECh. 10.4 - Does each of these lists of vertices form a path...Ch. 10.4 - Does each of these lists of vertices form a path...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - How many connected components does each of the...Ch. 10.4 - What do the connected components of...Ch. 10.4 - Prob. 8ECh. 10.4 - Explain why in the collaboration graph of...Ch. 10.4 - In the Hollywood graph (see Example 3 inSection...Ch. 10.4 - Determine whether each of these graphs is strongly...Ch. 10.4 - Determine whether each of these graphs is strongly...Ch. 10.4 - What do the strongly connected components of a...Ch. 10.4 - Find the strongly connected components of each of...Ch. 10.4 - Find the strongly connected components of each of...Ch. 10.4 - Suppose that G=(V, E) is a directed graph. A...Ch. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Find the number of paths of length n between two...Ch. 10.4 - Use paths either to show that these graphs are not...Ch. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Find the number of paths of length n between any...Ch. 10.4 - Find the number of paths of length n between any...Ch. 10.4 - Find the number of paths between c andd inthe...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Show that in every simple graph there is a path...Ch. 10.4 - In Exercises 31-33 find all the cut vertices of...Ch. 10.4 - In Exercises 31-33 find all the cut vertices of...Ch. 10.4 - Prob. 33ECh. 10.4 - Find all the cut edges in the graph sin Exercises...Ch. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - A vertex basis in a directed graph G is aminimal...Ch. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Use Exercise43 to show that a simple graph with n...Ch. 10.4 - Show that a simple graph G withnvertices is...Ch. 10.4 - Prob. 46ECh. 10.4 - How many nonisom orphic connected simple graphs...Ch. 10.4 - Show that each of the following graphs has no cut...Ch. 10.4 - Prob. 49ECh. 10.4 - For each of these graphs, find(G),(G),and...Ch. 10.4 - Show that if G is a connected graph, then it is...Ch. 10.4 - Show that if G is a connected graph withnvertices...Ch. 10.4 - Find(Km,n) and(Km,n), wherem andnare positive...Ch. 10.4 - Construct a graphG with(G) - 1,(G) -2, and...Ch. 10.4 - Show that if G is a graph, then(G) (G).Ch. 10.4 - ExplainhowTheorem 2canbe used to find the length...Ch. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 59ECh. 10.4 - Show that the existence of a simple circuit of...Ch. 10.4 - Prob. 61ECh. 10.4 - Use Exercise 61 to show that the...Ch. 10.4 - Prob. 63ECh. 10.4 - In an old puzzle attributed to Alcuin of York...Ch. 10.4 - Use a graph model and a path in your graph, as in...Ch. 10.4 - Prob. 66ECh. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - Prob. 3ECh. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - Suppose that in addition to the seven bridges of...Ch. 10.5 - Prob. 10ECh. 10.5 - When can the centerlines of the streets in a city...Ch. 10.5 - Devise a procedure, similar to Algorithm 1, for...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - Show that a directed multigraph having no isolated...Ch. 10.5 - Show that a directed multigraph having no isolated...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - Devise an algorithm for constructing Euler...Ch. 10.5 - Devise an algorithm for constructing Euler paths...Ch. 10.5 - For which values of n do thesegraphs have an...Ch. 10.5 - For whichvalues ofndo the graphs in Exercise 26...Ch. 10.5 - For which values ofmandn.does the complete...Ch. 10.5 - Find the least number of times it is necessary to...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - Prob. 35ECh. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - Does the graph in Exercise 30 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 31 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 32 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 33 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 34 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 35 have a Hamilton...Ch. 10.5 - Does the graph inExercise 36 have a Hamilton path?...Ch. 10.5 - For which values ofn.do the graphs in Exercise 26...Ch. 10.5 - For which values of m andndoes the complete...Ch. 10.5 - Show that thePetersen graph,shown here, does not...Ch. 10.5 - For each of these graphs, determine (i) whether...Ch. 10.5 - Can you find a simple graph with n vertices...Ch. 10.5 - Show that there is a Gray code of order whenever n...Ch. 10.5 - Fleury’s algorithm, published in 1883, constricts...Ch. 10.5 - Express Fleury's algorithm in pseudocode.Ch. 10.5 - Prob. 52ECh. 10.5 - Give a variant of Fleury's algorithm to produce...Ch. 10.5 - A diagnostic message can be sent out over a...Ch. 10.5 - Show that a bipartite graph with an odd number of...Ch. 10.5 - A knightis a chess piece that can move either two...Ch. 10.5 - A knightis a chess piece that can move either two...Ch. 10.5 - a) Show that finding a knights tour on...Ch. 10.5 - Show that there is a knight's tour on...Ch. 10.5 - Show that there is no knight's tour on...Ch. 10.5 - Show that there is no knight's tour on...Ch. 10.5 - Show that the graph representing the 1egal moves...Ch. 10.5 - Show that there is no reentrant knight's tour on...Ch. 10.5 - Show that there is a knight's tour on...Ch. 10.5 - The parts of this exercise outline a proof of...Ch. 10.5 - Show that if u and v are nondjacent vertices in a...Ch. 10.5 - Show that this graph doesnothave a Hamilton...Ch. 10.5 - Prob. 68ECh. 10.6 - For each of these problems about a subway system,...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - Find a shortest path betweenaandzin each of the...Ch. 10.6 - Prob. 6ECh. 10.6 - Find shortest paths in the weighted graph in...Ch. 10.6 - Find a shortest path (in mileage) between each of...Ch. 10.6 - Find a combination of flights with the least total...Ch. 10.6 - Find a least expensive combination of flights...Ch. 10.6 - Find a shortest route (in distance) between...Ch. 10.6 - Find a routs with the shortest response time...Ch. 10.6 - Find a least expensive route, in monthly lease...Ch. 10.6 - Explain how to find a path mm the least number of...Ch. 10.6 - Exend Dijkstea's algorithm for finding the length...Ch. 10.6 - Extend Dijkstra's algorithm for finding the length...Ch. 10.6 - The weighted graphs in the figures here show some...Ch. 10.6 - Is a shortest path between two vertices in a...Ch. 10.6 - What are some applications where it is necessary...Ch. 10.6 - What is the length of a longest simple path in the...Ch. 10.6 - Floyd 's algorithm,displayed as Algorithm 2, can...Ch. 10.6 - Prove that Floyd's algorithm determines the...Ch. 10.6 - Give a big-0 estimate of the number of operations...Ch. 10.6 - Show that Dijkstra's algorithm may not work if...Ch. 10.6 - Solve the traveling salesperson problem for this...Ch. 10.6 - Solve the traveling salesperson problem far this...Ch. 10.6 - Find a route with the least total airfare that...Ch. 10.6 - Find a route with the least total airfare that...Ch. 10.6 - Construct a weighted undirected graph such that...Ch. 10.6 - Show that the problem of finding a circuit of...Ch. 10.6 - The longest path problemin a weighted directed...Ch. 10.7 - Can five houses be connected to two utilities...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - Complete the argument inExample 3.Ch. 10.7 - Show thatK5is nonplanar using an argument similar...Ch. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - ProveCorollary 3.Ch. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Suppose that a planar graph haskconnected...Ch. 10.7 - Which of these nonplanar graphs have the property...Ch. 10.7 - Prob. 20ECh. 10.7 - In Exercises 20-22 determine whether the given...Ch. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Show thatK3,3has 2 as its thickness.Ch. 10.7 - Find the thickness of the graphs in Exercise 27.Ch. 10.7 - Show that ifGis a connected simple graph...Ch. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Draw K3,3on the surface of a torus so that no...Ch. 10.8 - Prob. 1ECh. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - What is the least number of colors needed to color...Ch. 10.8 - Prob. 15ECh. 10.8 - Show that a simple graph that has a circuit with...Ch. 10.8 - Schedule the final exams for Math 115, Math 116,...Ch. 10.8 - How many different channels are needed for six...Ch. 10.8 - The mathematics department has six committees,...Ch. 10.8 - Prob. 20ECh. 10.8 - Find the edge chromatic number of each of the...Ch. 10.8 - Prob. 22ECh. 10.8 - Find the edge chromatic numbers of a)Cn,wheren3....Ch. 10.8 - Prob. 24ECh. 10.8 - Show that ifGis a graph withnvertices, there no...Ch. 10.8 - Find the edge chromatic number ofKnwhen n is a...Ch. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Construct a coloring of the graph shown using this...Ch. 10.8 - Use pseudocode to describe this coloring...Ch. 10.8 - Show that the coloring produced by this algorithm...Ch. 10.8 - Show thatCnis chromatically 3-critical whenevernis...Ch. 10.8 - Show thatWnis chromatically 4-critical whenever n...Ch. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Find these values: a)X2(K3) b)X2(K4) c) X2(W4)...Ch. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Frequencies for mobile radio (or cellular)...Ch. 10.8 - Show that every planar graph G can be colored...Ch. 10.8 - Prob. 41ECh. 10.8 - Show that g(3) = 1 and g(4) = 1 by showing that...Ch. 10.8 - Show that g(5) = 1. That is, show that all...Ch. 10.8 - Show that g(6) = 2by first using Exercises 42 and...Ch. 10.8 - Prob. 45ECh. 10.8 - Solve the art gallery problem by proving theart...Ch. 10 - a) Define a simple graph, a multigraph, a...Ch. 10 - Prob. 2RQCh. 10 - What is the relationship between the sum of the...Ch. 10 - Why must there be an even number of vertices of...Ch. 10 - Prob. 5RQCh. 10 - Describe the following families of graphs....Ch. 10 - Prob. 7RQCh. 10 - Prob. 8RQCh. 10 - a) Describe three different methods that can be...Ch. 10 - a) What does it mean for two simple graphs to be...Ch. 10 - a) What does it mean for a graph to be connected?...Ch. 10 - Prob. 12RQCh. 10 - a) Define an Euler circuit and an Euler path in an...Ch. 10 - Prob. 14RQCh. 10 - Give examples of at least two problems that can be...Ch. 10 - a) Describe Dijkstra's algorithm for finding the...Ch. 10 - a) What does it mean for a graph to be planar? b)...Ch. 10 - a) What is Eider's formula for connected planar...Ch. 10 - Prob. 19RQCh. 10 - a) Define the chromatic number of a graph. b) What...Ch. 10 - Prob. 21RQCh. 10 - Prob. 22RQCh. 10 - Prob. 1SECh. 10 - How many nonisomorphic subgraphs doesK3have?Ch. 10 - Prob. 3SECh. 10 - Prob. 4SECh. 10 - Prob. 5SECh. 10 - Prob. 6SECh. 10 - Prob. 7SECh. 10 - Prob. 8SECh. 10 - LetG= (V, E)be an undirected graph and let...Ch. 10 - Prob. 10SECh. 10 - Prob. 11SECh. 10 - Prob. 12SECh. 10 - Prob. 13SECh. 10 - Prob. 14SECh. 10 - We say that three verticesu, v, andwof a simple...Ch. 10 - Find the clustering coefficient of each of the...Ch. 10 - Prob. 17SECh. 10 - For each of the graphs in Exercise 17, explain...Ch. 10 - Prob. 19SECh. 10 - A cliquein a simple undirected graph is a complete...Ch. 10 - Prob. 21SECh. 10 - Prob. 22SECh. 10 - Prob. 23SECh. 10 - Prob. 24SECh. 10 - Prob. 25SECh. 10 - Prob. 26SECh. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - Prob. 31SECh. 10 - A simple graph can be used to determine the...Ch. 10 - Prob. 33SECh. 10 - Prob. 34SECh. 10 - Prob. 35SECh. 10 - Prob. 36SECh. 10 - An orientationof an undirected simple graph is an...Ch. 10 - Prob. 38SECh. 10 - Prob. 39SECh. 10 - A tournament is a simple directed graph such that...Ch. 10 - Prob. 41SECh. 10 - A tournamentis a simple directed graph such that...Ch. 10 - Prob. 43SECh. 10 - Prob. 44SECh. 10 - Prob. 45SECh. 10 - Prob. 46SECh. 10 - A connected graphG = (V, E)withnvertices and m...Ch. 10 - A connected graphG = (V, E)withnvertices and m...Ch. 10 - Prob. 49SECh. 10 - Prob. 50SECh. 10 - Prob. 51SECh. 10 - Thedistancebetween two distinct verticesv1and v2of...Ch. 10 - a) Show that if the diameter of the simple graph G...Ch. 10 - Prob. 54SECh. 10 - Prob. 55SECh. 10 - Devise an algorithm for finding the second...Ch. 10 - Prob. 57SECh. 10 - Prob. 58SECh. 10 - Show that ifGis a simple graph with at least 11...Ch. 10 - Prob. 60SECh. 10 - Prob. 61SECh. 10 - Show that the chromatic number of a graph is less...Ch. 10 - Suppose that to generate a random simple graph...Ch. 10 - For each of these properties, determine whether it...Ch. 10 - Prob. 65SECh. 10 - Prob. 66SECh. 10 - Prob. 1CPCh. 10 - Prob. 2CPCh. 10 - Prob. 3CPCh. 10 - Prob. 4CPCh. 10 - Prob. 5CPCh. 10 - Prob. 6CPCh. 10 - Prob. 7CPCh. 10 - Prob. 8CPCh. 10 - Given, a positive integer n, generate a simple...Ch. 10 - Prob. 10CPCh. 10 - Prob. 11CPCh. 10 - Prob. 12CPCh. 10 - Given the vertex pairs associated to the edges of...Ch. 10 - Given the ordered pairs of vertices associated to...Ch. 10 - Given the list of edges of a simple graph, produce...Ch. 10 - Given the list of edges of a simple graph, produce...Ch. 10 - Given the list of edges and weights of these edges...Ch. 10 - Given the list of edges of an undirected graph,...Ch. 10 - Prob. 19CPCh. 10 - Given the distances between pairs of television...Ch. 10 - Prob. 1CAECh. 10 - Prob. 2CAECh. 10 - Prob. 3CAECh. 10 - Prob. 4CAECh. 10 - Prob. 5CAECh. 10 - Prob. 6CAECh. 10 - Prob. 7CAECh. 10 - Prob. 8CAECh. 10 - Generate at random simple graphs with 10 vertices....Ch. 10 - Generate at random simple graphs with 10 vertices....Ch. 10 - Find the chromatic number of each of the graphs...Ch. 10 - Find the shortest path a traveling salesperson can...Ch. 10 - Prob. 13CAECh. 10 - Prob. 14CAECh. 10 - Describe the origins and development of graph...Ch. 10 - Prob. 2WPCh. 10 - Discuss the applications of graph theory to...Ch. 10 - Prob. 4WPCh. 10 - Explain what community structure is in a graph...Ch. 10 - Describe some of the algorithms used to detect...Ch. 10 - Prob. 7WPCh. 10 - Explain how graph theory can help uncover networks...Ch. 10 - Prob. 9WPCh. 10 - Prob. 10WPCh. 10 - Prob. 11WPCh. 10 - Prob. 12WPCh. 10 - Describe how Euler paths can be used to help...Ch. 10 - Prob. 14WPCh. 10 - Describe theChinese postman problemand explain how...Ch. 10 - Describe some of the different conditions that...Ch. 10 - Prob. 17WPCh. 10 - Prob. 18WPCh. 10 - In modeling, very large scale integration (VLSI)...Ch. 10 - Prob. 20WPCh. 10 - Prob. 21WPCh. 10 - Describe and compare several different algorithms...Ch. 10 - Explain how graph multicolorings can be used in a...Ch. 10 - Prob. 24WPCh. 10 - Explain how the theory of random graphs can be...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 1. Suppose F(t) gives the temperature in degrees Fahrenheit t minutes after 1pm. With a complete sentence, interpret the equation F(10) 68. (Remember this means explaining the meaning of the equation without using any mathy vocabulary!) Include units. (3 points) =arrow_forward2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below. a. Evaluate f(-3). If you have multiple steps, be sure to connect your expressions with EQUALS SIGNS. (3 points)arrow_forwardPls help asap on all asked questions. pls show all work and steps.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY