Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
8th Edition
ISBN: 9781259676512
Author: Kenneth H Rosen
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10.3, Problem 24E
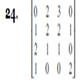
In Exercises22-24 draw the graph represented by the given adjacency matrix.
The density of an undirected graph G is the number of edges of G divided by the number of possible edges in an undirected graph with | G| vertices, Consequent, the density of G(V,E) is
A family of graphs Gn, n = 1, 2,... issparseif the limit of the density of Gnis zero as n grows without bound, while it is dense if this proportion approaches a positive real number. As mentioned in the text, an individual graph is called sparse when it contains relatively few edges and dense if it contains many edges. These terms can be defined precisely depending on the contest, but different definitions generally will not agree.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
For context, the image attached below is a question from a June 2024 past paper in statisical modeling
For context, the images attached below are a question from a June, 2024 past paper in statistical modeling
For context, the images attached below (question and related graph) are from a February 2024 past paper in statistical modeling
Chapter 10 Solutions
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
Ch. 10.1 - Draw graph models, stating the type of graph...Ch. 10.1 - Prob. 2ECh. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For Exercises 3-5, determine whether the graph...Ch. 10.1 - For each undirected graph in Exercises 3-9 that is...
Ch. 10.1 - Let G be a simple graph. Show that the relation R...Ch. 10.1 - Let G be an undirected graph with a loop at every...Ch. 10.1 - The intersection graphof a collection of...Ch. 10.1 - Use the niche overlap graph inFigure 11to...Ch. 10.1 - Construct a niche overlap graph for six species of...Ch. 10.1 - Draw the acquaintanceship graph that represents...Ch. 10.1 - Prob. 17ECh. 10.1 - Who can influence Fred and whom can Fred influence...Ch. 10.1 - Construct an influence graph for the board members...Ch. 10.1 - The word apple can refer to a plant, a food, or a...Ch. 10.1 - Prob. 21ECh. 10.1 - Which other teams did Team 4 beat and which teams...Ch. 10.1 - In a round-robin tournament the Tigers beat the...Ch. 10.1 - Construct the call graph for a set of seven...Ch. 10.1 - Explain how the two telephone call graphs for...Ch. 10.1 - a) Explain how graphs can be used to model...Ch. 10.1 - How can a graph that models e-mail messages sent...Ch. 10.1 - How can a graph that models e-mail messages sent...Ch. 10.1 - Describe a graph model that represents whether...Ch. 10.1 - Describe a graph model that represents a subway...Ch. 10.1 - Prob. 31ECh. 10.1 - Describe a graph model that represents the...Ch. 10.1 - Describe a graph model that represents traditional...Ch. 10.1 - Prob. 34ECh. 10.1 - Construct a precedence graph for the following...Ch. 10.1 - Describe a discrete structure based on a graph...Ch. 10.1 - Describe a discrete structure based on a graph...Ch. 10.1 - Prob. 38ECh. 10.2 - In Exercises 1-3 find the number of vertices, the...Ch. 10.2 - In Exercises 1-3 find the number of vertices, the...Ch. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Can a simple graph exist with 15 vertices each of...Ch. 10.2 - Show that the sum, over the set of people at a...Ch. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - For each of the graphs in Exercises 7-9 determine...Ch. 10.2 - Construct the underlying undirected graph for the...Ch. 10.2 - What does the degree of a vertex represent in the...Ch. 10.2 - Prob. 13ECh. 10.2 - What does the degree of a vertex in the Hollywood...Ch. 10.2 - What do the in-degree and the out-degree of a...Ch. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Show that in a simple graph with at least two...Ch. 10.2 - Use Exercise 18 to show that in a group of people,...Ch. 10.2 - Prob. 20ECh. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - In Exercises 21-25 determine whether the graph is...Ch. 10.2 - For which values ofnare these graphs bipartite?...Ch. 10.2 - Suppose that therearefour employees in the...Ch. 10.2 - Suppose that a new company has five employees:...Ch. 10.2 - Suppose that therearefive young women and five...Ch. 10.2 - Suppose that therearefive young women and six...Ch. 10.2 - Prob. 31ECh. 10.2 - Each of Exercises 31-33 can be solved using Hall's...Ch. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Each of Exercises 31-33 can be solved using Hall's...Ch. 10.2 - Prob. 36ECh. 10.2 - How many vertices and how many edges do these...Ch. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - How many edges does a graph have if its degree...Ch. 10.2 - Prob. 43ECh. 10.2 - Determine whether each of these sequences is...Ch. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Draw all sub graphs of this graph.Ch. 10.2 - Let G be a graph with vertices and e edges. Let M...Ch. 10.2 - For which values ofnare these graphs regular? a)...Ch. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - In Exercises 58-60 find the union of the given...Ch. 10.2 - Prob. 59ECh. 10.2 - In Exercises 58-60 find the union of the given...Ch. 10.2 - The complementarygraphGof a simple graph G has the...Ch. 10.2 - IfGis a simple graph with 15 edges andGhas 13...Ch. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Describe an algorithm to decide whether a graph is...Ch. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.2 - Prob. 74ECh. 10.2 - Theconverseof a directed graph G = (V, E), denoted...Ch. 10.3 - In Exercises 1-4 use an adjacency list to...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Represent the graph in Exercise 1 with an...Ch. 10.3 - Represent the graph in Exercise 2 with an...Ch. 10.3 - Represent the graph in Exercise 3 with an...Ch. 10.3 - Represent the graph in Exercise 4 with an...Ch. 10.3 - Represent each of these graphs with an adjacency...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 10-12 draw a graph with the given...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 13-15 represent the given graph using...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - In Exercises 16-18 draw an undirected graph...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19-21 find the adjacency matrix of...Ch. 10.3 - In Exercises 19-21 find the adjacency matrix of...Ch. 10.3 - In Exercises 22-24 draw the graph represented by...Ch. 10.3 - In Exercises 22-24 draw the graph represented by...Ch. 10.3 - In Exercises22-24 draw the graph represented by...Ch. 10.3 - Find the density of the graph in a)Figure...Ch. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Is every zero-one square matrix that is symmetric...Ch. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - What is me sum of me entries in a column of me...Ch. 10.3 - What is the sum of the entries in a row of the...Ch. 10.3 - What is the sum of the entries in a column of the...Ch. 10.3 - Find an adjacency matrix for each of these graphs....Ch. 10.3 - Prob. 37ECh. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - In Exercises 38-48 determine whether the given...Ch. 10.3 - Show that isomorphism of simple graphs is an...Ch. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - How many non isomorphic simple graphs are there...Ch. 10.3 - How many nonisomorphic simple graphs are there...Ch. 10.3 - How many nonisomorphic simple graphs are there...Ch. 10.3 - Prob. 61ECh. 10.3 - Prob. 62ECh. 10.3 - Are the simple graphswiththe following adjacency...Ch. 10.3 - Determine whether the graphs without loops with...Ch. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - In Exercises 67-70 determine whether the given...Ch. 10.3 - Prob. 69ECh. 10.3 - In Exercises 67-70 determine whether the given...Ch. 10.3 - Show that ifGand H are isomorphic directed graphs,...Ch. 10.3 - Show that the property that a graph is bipartite...Ch. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - How much storage is needed to represent a simple...Ch. 10.3 - A devil's pairfor a purported isomorphism testis a...Ch. 10.3 - Prob. 78ECh. 10.4 - Does each of these lists of vertices form a path...Ch. 10.4 - Does each of these lists of vertices form a path...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - In Exercises 3-5 determine whether the given graph...Ch. 10.4 - How many connected components does each of the...Ch. 10.4 - What do the connected components of...Ch. 10.4 - Prob. 8ECh. 10.4 - Explain why in the collaboration graph of...Ch. 10.4 - In the Hollywood graph (see Example 3 inSection...Ch. 10.4 - Determine whether each of these graphs is strongly...Ch. 10.4 - Determine whether each of these graphs is strongly...Ch. 10.4 - What do the strongly connected components of a...Ch. 10.4 - Find the strongly connected components of each of...Ch. 10.4 - Find the strongly connected components of each of...Ch. 10.4 - Suppose that G=(V, E) is a directed graph. A...Ch. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Find the number of paths of length n between two...Ch. 10.4 - Use paths either to show that these graphs are not...Ch. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Find the number of paths of length n between any...Ch. 10.4 - Find the number of paths of length n between any...Ch. 10.4 - Find the number of paths between c andd inthe...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Show that in every simple graph there is a path...Ch. 10.4 - In Exercises 31-33 find all the cut vertices of...Ch. 10.4 - In Exercises 31-33 find all the cut vertices of...Ch. 10.4 - Prob. 33ECh. 10.4 - Find all the cut edges in the graph sin Exercises...Ch. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - A vertex basis in a directed graph G is aminimal...Ch. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Use Exercise43 to show that a simple graph with n...Ch. 10.4 - Show that a simple graph G withnvertices is...Ch. 10.4 - Prob. 46ECh. 10.4 - How many nonisom orphic connected simple graphs...Ch. 10.4 - Show that each of the following graphs has no cut...Ch. 10.4 - Prob. 49ECh. 10.4 - For each of these graphs, find(G),(G),and...Ch. 10.4 - Show that if G is a connected graph, then it is...Ch. 10.4 - Show that if G is a connected graph withnvertices...Ch. 10.4 - Find(Km,n) and(Km,n), wherem andnare positive...Ch. 10.4 - Construct a graphG with(G) - 1,(G) -2, and...Ch. 10.4 - Show that if G is a graph, then(G) (G).Ch. 10.4 - ExplainhowTheorem 2canbe used to find the length...Ch. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 59ECh. 10.4 - Show that the existence of a simple circuit of...Ch. 10.4 - Prob. 61ECh. 10.4 - Use Exercise 61 to show that the...Ch. 10.4 - Prob. 63ECh. 10.4 - In an old puzzle attributed to Alcuin of York...Ch. 10.4 - Use a graph model and a path in your graph, as in...Ch. 10.4 - Prob. 66ECh. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - Prob. 3ECh. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - In Exercises 1-8 determine whether the given graph...Ch. 10.5 - Suppose that in addition to the seven bridges of...Ch. 10.5 - Prob. 10ECh. 10.5 - When can the centerlines of the streets in a city...Ch. 10.5 - Devise a procedure, similar to Algorithm 1, for...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - In Exercises 13-15 determine whether the picture...Ch. 10.5 - Show that a directed multigraph having no isolated...Ch. 10.5 - Show that a directed multigraph having no isolated...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - In Exercises 18-23 determine whether the directed...Ch. 10.5 - Devise an algorithm for constructing Euler...Ch. 10.5 - Devise an algorithm for constructing Euler paths...Ch. 10.5 - For which values of n do thesegraphs have an...Ch. 10.5 - For whichvalues ofndo the graphs in Exercise 26...Ch. 10.5 - For which values ofmandn.does the complete...Ch. 10.5 - Find the least number of times it is necessary to...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - Prob. 35ECh. 10.5 - In Exercises 30-36 determine whether the given...Ch. 10.5 - Does the graph in Exercise 30 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 31 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 32 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 33 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 34 have a Hamilton...Ch. 10.5 - Does the graph in Exercise 35 have a Hamilton...Ch. 10.5 - Does the graph inExercise 36 have a Hamilton path?...Ch. 10.5 - For which values ofn.do the graphs in Exercise 26...Ch. 10.5 - For which values of m andndoes the complete...Ch. 10.5 - Show that thePetersen graph,shown here, does not...Ch. 10.5 - For each of these graphs, determine (i) whether...Ch. 10.5 - Can you find a simple graph with n vertices...Ch. 10.5 - Show that there is a Gray code of order whenever n...Ch. 10.5 - Fleury’s algorithm, published in 1883, constricts...Ch. 10.5 - Express Fleury's algorithm in pseudocode.Ch. 10.5 - Prob. 52ECh. 10.5 - Give a variant of Fleury's algorithm to produce...Ch. 10.5 - A diagnostic message can be sent out over a...Ch. 10.5 - Show that a bipartite graph with an odd number of...Ch. 10.5 - A knightis a chess piece that can move either two...Ch. 10.5 - A knightis a chess piece that can move either two...Ch. 10.5 - a) Show that finding a knights tour on...Ch. 10.5 - Show that there is a knight's tour on...Ch. 10.5 - Show that there is no knight's tour on...Ch. 10.5 - Show that there is no knight's tour on...Ch. 10.5 - Show that the graph representing the 1egal moves...Ch. 10.5 - Show that there is no reentrant knight's tour on...Ch. 10.5 - Show that there is a knight's tour on...Ch. 10.5 - The parts of this exercise outline a proof of...Ch. 10.5 - Show that if u and v are nondjacent vertices in a...Ch. 10.5 - Show that this graph doesnothave a Hamilton...Ch. 10.5 - Prob. 68ECh. 10.6 - For each of these problems about a subway system,...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - In Exercises 2-4 find the length of a shortest...Ch. 10.6 - Find a shortest path betweenaandzin each of the...Ch. 10.6 - Prob. 6ECh. 10.6 - Find shortest paths in the weighted graph in...Ch. 10.6 - Find a shortest path (in mileage) between each of...Ch. 10.6 - Find a combination of flights with the least total...Ch. 10.6 - Find a least expensive combination of flights...Ch. 10.6 - Find a shortest route (in distance) between...Ch. 10.6 - Find a routs with the shortest response time...Ch. 10.6 - Find a least expensive route, in monthly lease...Ch. 10.6 - Explain how to find a path mm the least number of...Ch. 10.6 - Exend Dijkstea's algorithm for finding the length...Ch. 10.6 - Extend Dijkstra's algorithm for finding the length...Ch. 10.6 - The weighted graphs in the figures here show some...Ch. 10.6 - Is a shortest path between two vertices in a...Ch. 10.6 - What are some applications where it is necessary...Ch. 10.6 - What is the length of a longest simple path in the...Ch. 10.6 - Floyd 's algorithm,displayed as Algorithm 2, can...Ch. 10.6 - Prove that Floyd's algorithm determines the...Ch. 10.6 - Give a big-0 estimate of the number of operations...Ch. 10.6 - Show that Dijkstra's algorithm may not work if...Ch. 10.6 - Solve the traveling salesperson problem for this...Ch. 10.6 - Solve the traveling salesperson problem far this...Ch. 10.6 - Find a route with the least total airfare that...Ch. 10.6 - Find a route with the least total airfare that...Ch. 10.6 - Construct a weighted undirected graph such that...Ch. 10.6 - Show that the problem of finding a circuit of...Ch. 10.6 - The longest path problemin a weighted directed...Ch. 10.7 - Can five houses be connected to two utilities...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 2-4 draw the given planar graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - In Exercises 5-9 determine whether the given graph...Ch. 10.7 - Complete the argument inExample 3.Ch. 10.7 - Show thatK5is nonplanar using an argument similar...Ch. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - ProveCorollary 3.Ch. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Suppose that a planar graph haskconnected...Ch. 10.7 - Which of these nonplanar graphs have the property...Ch. 10.7 - Prob. 20ECh. 10.7 - In Exercises 20-22 determine whether the given...Ch. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Show thatK3,3has 2 as its thickness.Ch. 10.7 - Find the thickness of the graphs in Exercise 27.Ch. 10.7 - Show that ifGis a connected simple graph...Ch. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Draw K3,3on the surface of a torus so that no...Ch. 10.8 - Prob. 1ECh. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - What is the least number of colors needed to color...Ch. 10.8 - Prob. 15ECh. 10.8 - Show that a simple graph that has a circuit with...Ch. 10.8 - Schedule the final exams for Math 115, Math 116,...Ch. 10.8 - How many different channels are needed for six...Ch. 10.8 - The mathematics department has six committees,...Ch. 10.8 - Prob. 20ECh. 10.8 - Find the edge chromatic number of each of the...Ch. 10.8 - Prob. 22ECh. 10.8 - Find the edge chromatic numbers of a)Cn,wheren3....Ch. 10.8 - Prob. 24ECh. 10.8 - Show that ifGis a graph withnvertices, there no...Ch. 10.8 - Find the edge chromatic number ofKnwhen n is a...Ch. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Construct a coloring of the graph shown using this...Ch. 10.8 - Use pseudocode to describe this coloring...Ch. 10.8 - Show that the coloring produced by this algorithm...Ch. 10.8 - Show thatCnis chromatically 3-critical whenevernis...Ch. 10.8 - Show thatWnis chromatically 4-critical whenever n...Ch. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Find these values: a)X2(K3) b)X2(K4) c) X2(W4)...Ch. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Frequencies for mobile radio (or cellular)...Ch. 10.8 - Show that every planar graph G can be colored...Ch. 10.8 - Prob. 41ECh. 10.8 - Show that g(3) = 1 and g(4) = 1 by showing that...Ch. 10.8 - Show that g(5) = 1. That is, show that all...Ch. 10.8 - Show that g(6) = 2by first using Exercises 42 and...Ch. 10.8 - Prob. 45ECh. 10.8 - Solve the art gallery problem by proving theart...Ch. 10 - a) Define a simple graph, a multigraph, a...Ch. 10 - Prob. 2RQCh. 10 - What is the relationship between the sum of the...Ch. 10 - Why must there be an even number of vertices of...Ch. 10 - Prob. 5RQCh. 10 - Describe the following families of graphs....Ch. 10 - Prob. 7RQCh. 10 - Prob. 8RQCh. 10 - a) Describe three different methods that can be...Ch. 10 - a) What does it mean for two simple graphs to be...Ch. 10 - a) What does it mean for a graph to be connected?...Ch. 10 - Prob. 12RQCh. 10 - a) Define an Euler circuit and an Euler path in an...Ch. 10 - Prob. 14RQCh. 10 - Give examples of at least two problems that can be...Ch. 10 - a) Describe Dijkstra's algorithm for finding the...Ch. 10 - a) What does it mean for a graph to be planar? b)...Ch. 10 - a) What is Eider's formula for connected planar...Ch. 10 - Prob. 19RQCh. 10 - a) Define the chromatic number of a graph. b) What...Ch. 10 - Prob. 21RQCh. 10 - Prob. 22RQCh. 10 - Prob. 1SECh. 10 - How many nonisomorphic subgraphs doesK3have?Ch. 10 - Prob. 3SECh. 10 - Prob. 4SECh. 10 - Prob. 5SECh. 10 - Prob. 6SECh. 10 - Prob. 7SECh. 10 - Prob. 8SECh. 10 - LetG= (V, E)be an undirected graph and let...Ch. 10 - Prob. 10SECh. 10 - Prob. 11SECh. 10 - Prob. 12SECh. 10 - Prob. 13SECh. 10 - Prob. 14SECh. 10 - We say that three verticesu, v, andwof a simple...Ch. 10 - Find the clustering coefficient of each of the...Ch. 10 - Prob. 17SECh. 10 - For each of the graphs in Exercise 17, explain...Ch. 10 - Prob. 19SECh. 10 - A cliquein a simple undirected graph is a complete...Ch. 10 - Prob. 21SECh. 10 - Prob. 22SECh. 10 - Prob. 23SECh. 10 - Prob. 24SECh. 10 - Prob. 25SECh. 10 - Prob. 26SECh. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - A simple graph can be used to determine the...Ch. 10 - Prob. 31SECh. 10 - A simple graph can be used to determine the...Ch. 10 - Prob. 33SECh. 10 - Prob. 34SECh. 10 - Prob. 35SECh. 10 - Prob. 36SECh. 10 - An orientationof an undirected simple graph is an...Ch. 10 - Prob. 38SECh. 10 - Prob. 39SECh. 10 - A tournament is a simple directed graph such that...Ch. 10 - Prob. 41SECh. 10 - A tournamentis a simple directed graph such that...Ch. 10 - Prob. 43SECh. 10 - Prob. 44SECh. 10 - Prob. 45SECh. 10 - Prob. 46SECh. 10 - A connected graphG = (V, E)withnvertices and m...Ch. 10 - A connected graphG = (V, E)withnvertices and m...Ch. 10 - Prob. 49SECh. 10 - Prob. 50SECh. 10 - Prob. 51SECh. 10 - Thedistancebetween two distinct verticesv1and v2of...Ch. 10 - a) Show that if the diameter of the simple graph G...Ch. 10 - Prob. 54SECh. 10 - Prob. 55SECh. 10 - Devise an algorithm for finding the second...Ch. 10 - Prob. 57SECh. 10 - Prob. 58SECh. 10 - Show that ifGis a simple graph with at least 11...Ch. 10 - Prob. 60SECh. 10 - Prob. 61SECh. 10 - Show that the chromatic number of a graph is less...Ch. 10 - Suppose that to generate a random simple graph...Ch. 10 - For each of these properties, determine whether it...Ch. 10 - Prob. 65SECh. 10 - Prob. 66SECh. 10 - Prob. 1CPCh. 10 - Prob. 2CPCh. 10 - Prob. 3CPCh. 10 - Prob. 4CPCh. 10 - Prob. 5CPCh. 10 - Prob. 6CPCh. 10 - Prob. 7CPCh. 10 - Prob. 8CPCh. 10 - Given, a positive integer n, generate a simple...Ch. 10 - Prob. 10CPCh. 10 - Prob. 11CPCh. 10 - Prob. 12CPCh. 10 - Given the vertex pairs associated to the edges of...Ch. 10 - Given the ordered pairs of vertices associated to...Ch. 10 - Given the list of edges of a simple graph, produce...Ch. 10 - Given the list of edges of a simple graph, produce...Ch. 10 - Given the list of edges and weights of these edges...Ch. 10 - Given the list of edges of an undirected graph,...Ch. 10 - Prob. 19CPCh. 10 - Given the distances between pairs of television...Ch. 10 - Prob. 1CAECh. 10 - Prob. 2CAECh. 10 - Prob. 3CAECh. 10 - Prob. 4CAECh. 10 - Prob. 5CAECh. 10 - Prob. 6CAECh. 10 - Prob. 7CAECh. 10 - Prob. 8CAECh. 10 - Generate at random simple graphs with 10 vertices....Ch. 10 - Generate at random simple graphs with 10 vertices....Ch. 10 - Find the chromatic number of each of the graphs...Ch. 10 - Find the shortest path a traveling salesperson can...Ch. 10 - Prob. 13CAECh. 10 - Prob. 14CAECh. 10 - Describe the origins and development of graph...Ch. 10 - Prob. 2WPCh. 10 - Discuss the applications of graph theory to...Ch. 10 - Prob. 4WPCh. 10 - Explain what community structure is in a graph...Ch. 10 - Describe some of the algorithms used to detect...Ch. 10 - Prob. 7WPCh. 10 - Explain how graph theory can help uncover networks...Ch. 10 - Prob. 9WPCh. 10 - Prob. 10WPCh. 10 - Prob. 11WPCh. 10 - Prob. 12WPCh. 10 - Describe how Euler paths can be used to help...Ch. 10 - Prob. 14WPCh. 10 - Describe theChinese postman problemand explain how...Ch. 10 - Describe some of the different conditions that...Ch. 10 - Prob. 17WPCh. 10 - Prob. 18WPCh. 10 - In modeling, very large scale integration (VLSI)...Ch. 10 - Prob. 20WPCh. 10 - Prob. 21WPCh. 10 - Describe and compare several different algorithms...Ch. 10 - Explain how graph multicolorings can be used in a...Ch. 10 - Prob. 24WPCh. 10 - Explain how the theory of random graphs can be...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For context, the images attached below are from a February 2024 past paper in statistical modelingarrow_forwardFor context, the image provided below is a question from a September, 2024 past paper in statistical modelingarrow_forwardFor context, the image below is from a January 2024 past paper in statistical modelingarrow_forward
- For context, the image provided below is a question from a September, 2024 past paper in statistical modelingarrow_forwardIf u use any type of chatgpt, will.downvote.arrow_forwardA function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forward
- Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward4 Use Cramer's rule to solve for x and t in the Lorentz-Einstein equations of special relativity:x^(')=\gamma (x-vt)t^(')=\gamma (t-v(x)/(c^(2)))where \gamma ^(2)(1-(v^(2))/(c^(2)))=1.arrow_forwardPls help on botharrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License