Chapter 10.5, Problem 53E

To determine

The pictures for an arbitrary N.

Answer to Problem 53E

It the integral converges, then the second inequality puts an upper bound on the partial sums to the series.

Explanation of Solution

Given information:

Relabel the pictures for an arbitrary N and explain why the same conclusions about convergence can be drawn.

Formula used:

  ${\displaystyle {\int }_N^{n+1}f\left(x\right)}dx<a_N+\mathrm{....}+a_n<a_N+{\displaystyle {\int }_N^{n}f\left(x\right)dx}$

Calculation:

The graphs are drawn for an arbitrary N as follows,

  

  

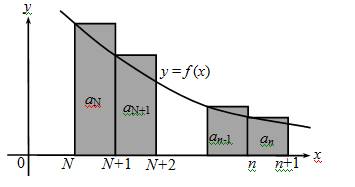
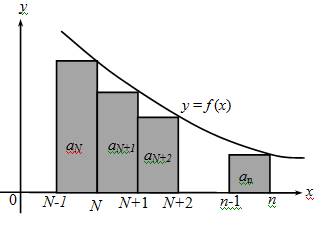
Comparing areas in the figures, we have for all $n\ge N$ , the sum $a_N+a_{N+1}+\mathrm{.....}+a_n$ provides an upper bound for ${\displaystyle {\int }_N^{n+1}f\left(x\right)}dx$ and the sum $a_{N+1}+a_{N+2}+\mathrm{.....}+a_n$ provides a lower bound for

  ${\displaystyle {\int }_N^{n}f\left(x\right)}dx$

So,

  ${\displaystyle {\int }_N^{n+1}f\left(x\right)}dx<a_N+\mathrm{....}+a_n<a_N+{\displaystyle {\int }_N^{n}f\left(x\right)dx}$

If the integral diverges, it must go to infinity, and the first inequality forces the partial sums of the series to go to infinity as well, so the series is divergent, It the integral converges, then the second inequality puts an upper bound on the partial sums to the series, and since they are a no deceasing sequence, they must converge to a finite sum of for the series.

Conclusion:

It the integral converges, then the second inequality puts an upper bound on the partial sums to the series.