Chapter 10.4, Problem 36E

Winter visitors are extremely important to the economy of Southwest Florida. Hotel occupancy is an often-reported measure of visitor volume and visitor activity (Naples Daily News, March 22, 2012). Hotel occupancy data for February in two consecutive years are as follows.

1. a. Formulate the hypothesis test that can be used to determine whether there has been an increase in the proportion of rooms occupied over the one-year period.
2. b. What is the estimated proportion of hotel rooms occupied each year?
3. c. Using a .05 level of significance, what is your hypothesis test conclusion? What is the p-value?
4. d. What is the 95% confidence interval estimate of the change in occupancy for the one-year period? Do you think area officials would be pleased with the results?

To determine

State the null and alternative hypotheses.

Answer to Problem 36E

Null hypothesis:$H_0:p_1-p_2\le 0$

Alternative hypothesis:$H_a:p_1-p_2>0$

Explanation of Solution

Calculation:

It is given that winter visitors are important to the economy of the southwest region of State F.

The given data is about the hotel room occupancy in the month of February in two consecutive years.

Here, $p_1$ represents the population proportion of rooms occupied for the current year and $p_2$ represents the population proportion of rooms occupied for the previous year.

State the hypothesis:

Null hypothesis:

$H_0:p_1-p_2\le 0$

That is, the proportion of rooms occupied in the current year is less than or equal to the proportion of rooms occupied in the previous year.

Alternative hypothesis:

$H_a:p_1-p_2>0$

That is, the proportion of rooms occupied in the current year is greater than the proportion of rooms occupied in the previous year.

To determine

Find the estimated proportion of hotel rooms occupied in each year.

Answer to Problem 36E

The estimated proportion of hotel rooms occupied in the current year is 0.84, and the estimated proportion of hotel rooms occupied in the previous year is 0.81.

Explanation of Solution

Calculation:

The estimated proportion of hotel rooms occupied in the current year is obtained as follows:

$\begin{array}{c}{\overline{p}}_1=\frac{x_1}{n_1}\\ =\frac{1,470}{1,750}\\ =0.84\end{array}$

Thus, the estimated proportion of hotel rooms occupied in the current year is 0.84.

The estimated proportion of hotel rooms occupied in the previous year is obtained as follows:

$\begin{array}{c}{\overline{p}}_2=\frac{x_2}{n_2}\\ =\frac{1,458}{1,800}\\ =0.81\end{array}$

Thus, the estimated proportion of hotel rooms occupied in the previous year is 0.81.

To determine

Find the p-value and provide a conclusion at $\alpha =0.05$ from the results.

Answer to Problem 36E

The p-value is 0.009.

There is sufficient evidence to conclude that the proportion of rooms occupied in the current year is greater than the previous year.

Explanation of Solution

Calculation:

The test statistic for hypothesis tests about $p_1-p_2$ is as follows:

$z=\frac{\left({\overline{p}}_1-{\overline{p}}_2\right)}{\sqrt{\overline{p}\left(1-\overline{p}\right)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$.

Here, ${\overline{p}}_1$ is the sample proportion for a simple random sample from population 1, ${\overline{p}}_2$ is the sample proportion for a simple random sample from population 2, $\overline{p}$ is the pooled estimator of p, $n_1$ is the sample size for population 1, $n_2$ is the sample size for population 2, and $z_{\frac{\alpha }{2}}$ is the critical value.

Pooled estimator:

$\begin{array}{c}\overline{p}=\frac{n_1{\overline{p}}_1+n_2{\overline{p}}_2}{n_1+n_2}\\ =\frac{1,750\left(0.84\right)+1,800\left(0.81\right)}{1,750+1,800}\\ =\frac{\text{2,928}}{\text{3,550}}\\ =0.8248\end{array}$

Substitute ${\overline{p}}_1$ as 0.84, ${\overline{p}}_2$ as 0.81, $n_1$ as 1,750, $n_2$ as 1,800, and $\overline{p}$ as 0.8248 in the z formula.

$\begin{array}{c}z=\frac{\left(0.84-0.81\right)}{\sqrt{0.8248\left(1-0.8248\right)\left(\frac{1}{1,750}+\frac{1}{1,800}\right)}}\\ =\frac{\text{0}\text{.03}}{\sqrt{\left(\text{0}\text{.14450496}\right)\left(\text{0}\text{.00113}\right)}}\\ =\frac{\text{0}\text{.03}}{\text{0}\text{.01278}}\\ =2.35\end{array}$

Thus, the test statistic z-value is 2.35.

Here, the test is a right tail test.

Software procedure:

Step-by-step procedure to obtain the probability value using Excel.

• Open an EXCEL sheet and select the cell A1.
• Enter the formula =1-NORM.S.DIST(2.35,TRUE) in the cell A1.
• Press Enter.

The output obtained using EXCEL software is given below:

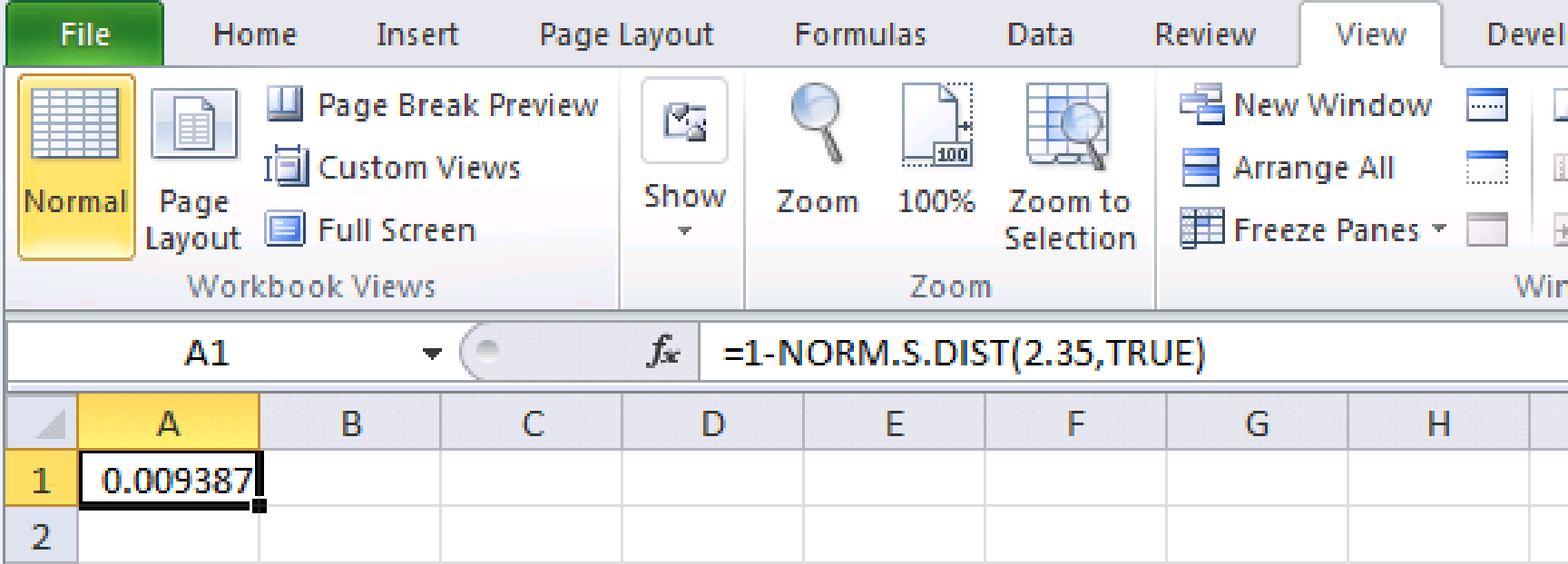
From the output, the p-value is approximately 0.009.

Rejection rule:

If the $p\text{-value}\le \alpha$, reject the null hypothesis.

If the $p\text{-value}>\alpha$, do not reject the null hypothesis.

Conclusion:

Here, the p-value is less than the level of significance.

That is, the $p\text{-value}\left(=0.009\right)<\alpha \left(=0.05\right)$.

From the rejection rule, the null hypothesis is rejected.

Therefore, there is sufficient evidence to conclude that the proportion of rooms occupied in the current year is greater than that in the previous year.

To determine

Obtain the 95% confidence interval estimate of the change in occupancy for the one-year period.

Explain whether the area officials are pleased with the results or not.

Answer to Problem 36E

The 95% confidence interval is $\left(0.005,0.055\right)$.

Yes, the area officials are pleased with the results.

Explanation of Solution

Calculation:

The formula for the confidence interval estimate of the difference between two populations is as follows:

${\overline{p}}_1-{\overline{p}}_2\pm z_{\frac{\alpha }{2}}\sqrt{\frac{{\overline{p}}_1\left(1-{\overline{p}}_1\right)}{n_1}+\frac{{\overline{p}}_2\left(1-{\overline{p}}_2\right)}{n_2}}$.

Here, ${\overline{p}}_1$ is the sample proportion for a simple random sample from population 1, ${\overline{p}}_2$ is the sample proportion for a simple random sample from population 2, $n_1$ is the sample size for population 1, $n_2$ is the sample size for population 2, and $z_{\frac{\alpha }{2}}$ is the critical value.

Critical value:

$\begin{array}{c}\alpha =0.05\\ \frac{\alpha }{2}=\frac{0.05}{2}\\ =0.025\end{array}$

The cumulative area to the left is obtained as follows:

$\begin{array}{c}\text{Area to the left}=1-\text{Area to the right}\\ =1-0.025\\ =0.975\end{array}$

Use Table 1: Cumulative probabilities for the standard Normal Distribution to find the critical value.

• Locate the area of 0.975 in the body of Table 1.
• Move left until the first column and note the values as 1.9.
• Move upward until the top row is reached and note the value as 0.06.

Thus, the value of $z_{0.025}$ is 1.96.

The 95% confidence interval estimate of the change in occupancy for the one-year period is obtained below:

$\begin{array}{c}{\overline{p}}_1-{\overline{p}}_2\pm z_{\frac{\alpha }{2}}\sqrt{\frac{{\overline{p}}_1\left(1-{\overline{p}}_1\right)}{n_1}+\frac{{\overline{p}}_2\left(1-{\overline{p}}_2\right)}{n_2}}=\left(0.84-0.81\right)\pm 1.96\sqrt{\frac{0.84\left(1-0.84\right)}{1,750}+\frac{0.81\left(1-0.81\right)}{1,800}}\\ =0.03\pm 1.96\sqrt{0.0000768+\text{0}\text{.0000855}}\\ =0.03\pm 1.96\left(0.0127\right)\\ =0.03\pm 0.025\end{array}$

                                                            $\begin{array}{c}=\left(0.03-0.025,0.03+0.025\right)\\ =\left(\text{0}\text{.005},\text{0}\text{.055}\right)\end{array}$

Thus, the 95% confidence interval is $\underset{\_}{\left(\text{0}\text{.005},\text{0}\text{.055}\right)}$.

Interpretation:

There is 95% chance that the proportion of increase in hotel room occupancy over the one-year period lies between 0.005 and 0.055.

Since there is an increase in the hotel occupancy rate, the officials are expected to be pleased with the occupancy rate.