Chapter 10.2, Problem 41P

The steel bar AB has a $\frac{3}{8}\times \frac{3}{8}$-in. square cross section and is held by pins that are a fixed distance apart and are located at a distance e = 0.03 in. from the geometric axis of the bar. Knowing that at temperature T₀ the pins are in contact with the bar and that the force in the bar is zero, determine the increase in temperature for which the bar will just make contact with point C if d = 0.01 in. Use E = 29 3 106 psi and a coefficient of thermal expansion α = 6.5 × 10^–6/°F.

Fig. P10.41

To determine

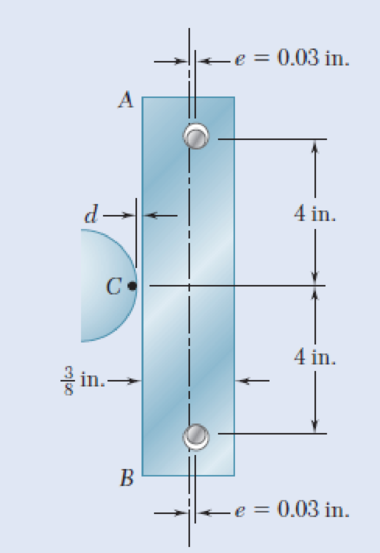
Find the increase in temperature.

Answer to Problem 41P

The increase in temperature required for the bar to make contact with the point C is $\underset{\_}{58.9°\text{F}}$.

Explanation of Solution

The centricity of the load in the column is $e=0.03\text{in}\text{.}$.

The distance between the bar and the pins is $d=0.01\text{in}\text{.}$.

The modulus of elasticity of the steel bar is $E=29\times {10}^6\text{psi}$.

The length of the column is $L=8\text{in}\text{.}$.

The coefficient of thermal expansion is $\alpha =6.5\times {10}^{-6}/°\text{F}$.

The dimension of the square cross section is $a=\frac{3}{8}\text{in}\text{.}$.

Find the moment of inertia of the square cross section (I) using the equation.

$I=\frac{a^4}{12}$

Here, the dimension of the square cross section is a.

Substitute $\frac{3}{8}\text{in}\text{.}$ for a.

$\begin{array}{c}I=\frac{{\left(\frac{3}{8}\right)}^4}{12}\\ =1.64795\times {10}^{-3}\text{in}{\text{.}}^3\end{array}$

The effective length of the column $\left(L_e\right)$ is equal to the length of the column (L).

$L_e=L=8\text{in}\text{.}$

Determine the critical load $\left(P_{\text{cr}}\right)$ using the equation.

$P_{cr}=\frac{{\pi }^{2}EI}{{\left(L_e\right)}^2}$

Here, the modulus of elasticity is E.

Substitute $29\times {10}^6\text{psi}$ for E, $1.64795\times {10}^{-3}\text{in}{\text{.}}^3$ for I, and 8 in. for $L_e$.

$\begin{array}{c}{P}_{\text{cr}}=\frac{{\pi }^2\times 29\times {10}^6\times 1.64795\times {10}^{-3}}{{\left(8\right)}^2}\\ =7,370\text{lb}\end{array}$

Determine the axial load P using the equation.

$y_m=d=e\left[\sec \left(\frac{\pi }{2}\sqrt{\frac{P}{P_{\text{cr}}}}\right)-1\right]$

Here, the deflection of the column is $y_m$, the distance between the bar and the pin is d, and the eccentricity of the load in the column is e.

Substitute 0.01 in. for d, 0.03 in. for e, and 7,370 lb for $P_{\text{cr}}$.

$\begin{array}{c}0.01=0.03\times \left[\sec \left(\frac{\pi }{2}\sqrt{\frac{P}{7,370}}\right)-1\right]\\ \sec \left(\frac{\pi }{2}\sqrt{\frac{P}{7,370}}\right)-1=\frac{1}{3}\\ \sec \left(\frac{\pi }{2}\sqrt{\frac{P}{7,370}}\right)=\frac{4}{3}\\ \cos \left(\frac{\pi }{2}\sqrt{\frac{P}{7,370}}\right)=\frac{3}{4}\end{array}$

$P=1,560.2\text{lb}$

Find the cross sectional area of the square cross section (A) as follows;

$A=a^2$

Substitute $\frac{3}{8}\text{in}\text{.}$ for a.

$\begin{array}{c}A={\left(\frac{3}{8}\right)}^2\\ =0.140625\text{in}{\text{.}}^2\end{array}$

Consider without the eccentricity of the load to find the temperature change;

Find the total elongation using the relation.

$\begin{array}{c}\text{Total}\text{elongation}={\left(\delta l\right)}_{thermal}-{\left(\delta l\right)}_{axial}\\ =\alpha L\left(\Delta T\right)-\frac{PL}{AE}\end{array}$

Here, the elongation due to thermal stress is ${\left(\delta l\right)}_{thermal}$, the elongation due to axial loads is ${\left(\delta l\right)}_{axial}$, the coefficient of thermal expansion is $\alpha$, and the change in temperature is $\Delta T$.

The total elongation in the column should be zero.

$\begin{array}{c}\text{Total}\text{elongation}=0\\ \alpha L\left(\Delta T\right)-\frac{PL}{AE}=0\\ \alpha L\left(\Delta T\right)=\frac{PL}{AE}\\ \Delta T=\frac{P}{AE\alpha }\end{array}$

Substitute 1,560.2 lb for P, $0.140625\text{in}{\text{.}}^2$ for A, $29\times {10}^6\text{psi}$ for E, and $6.5\times {10}^{-6}/°\text{F}$ for $\alpha$.

$\begin{array}{c}\Delta T=\frac{1,560.2}{0.140625\times 29\times {10}^6\times 6.5\times {10}^{-6}}\\ =58.9°\text{F}\end{array}$

Consider the eccentricity to find the temperature change;

Find the total elongation in the column using the relation.

$\text{Total}\text{elongation}=\alpha L\left(\Delta T\right)-\frac{PL}{AE}={2e\frac{dy}{dx}|}_{x=0}$ (1)

Refer to Equation (10.26) in the textbook.

Apply the elastic curve equation;

$y=e\left(\tan \frac{pL}{2}\sin px+\cos px-1\right)$

Differentiate the equation.

$\frac{dy}{dx}=e\left(p\tan \frac{pL}{2}\cos px-p\sin px\right)$

When the distance $x=0$.

$\begin{array}{c}{\frac{dy}{dx}|}_{x=0}=e\left(p\tan \frac{pL}{2}\cos p\left(0\right)-p\sin p\left(0\right)\right)\\ =ep\tan \frac{pL}{2}\end{array}$ (2)

Refer to Equation (10.6) in the textbook.

$\begin{array}{l}{p}^2=\frac{P}{EI}\\ p=\sqrt{\frac{P}{EI}}\end{array}$

The critical load is given by the equation.

$\begin{array}{l}{P}_{\text{cr}}=\frac{{\pi }^{2}EI}{L^2}\\ L=\frac{\pi \sqrt{EI}}{\sqrt{P_{\text{cr}}}}\end{array}$

Substitute $\sqrt{\frac{P}{EI}}$ for p and $\frac{\pi \sqrt{EI}}{\sqrt{P_{\text{cr}}}}$ for L in Equation (2).

$\begin{array}{c}{\frac{dy}{dx}|}_{x=0}=e\sqrt{\frac{P}{EI}}\tan \frac{\sqrt{\frac{P}{EI}}\times \frac{\pi \sqrt{EI}}{\sqrt{P_{\text{cr}}}}}{2}\\ =e\sqrt{\frac{P}{EI}}\tan \frac{\pi }{2}\sqrt{\frac{P}{P_{\text{cr}}}}\end{array}$

Substitute $e\sqrt{\frac{P}{EI}}\tan \frac{\pi }{2}\sqrt{\frac{P}{P_{\text{cr}}}}$ for ${\frac{dy}{dx}|}_{x=0}$ in Equation (1).

$\alpha L\left(\Delta T\right)-\frac{PL}{AE}=2e\left(e\sqrt{\frac{P}{EI}}\tan \frac{\pi }{2}\sqrt{\frac{P}{P_{\text{cr}}}}\right)$

Substitute 1,560.2 lb for P, 7,370 lb for $P_{\text{cr}}$, 8 in. for L, $0.140625\text{in}{\text{.}}^2$ for A, $29\times {10}^6\text{psi}$ for E, $1.64795\times {10}^{-3}\text{in}{\text{.}}^3$ for I, $6.5\times {10}^{-6}/°\text{F}$ for $\alpha$, and 0.03 in. for e.

$\begin{array}{l}6.5\times {10}^{-6}\times 8\times \left(\Delta T\right)-\frac{1,560.2\times 8}{0.140625\times 29\times {10}^6}=2\times {0.03}^2\times \sqrt{\frac{1,560.2}{29\times {10}^6\times 1.64795\times {10}^{-3}}}\tan \frac{\pi }{2}\sqrt{\frac{1,560.2}{7,370}}\\ 52\times {10}^{-6}\left(\Delta T\right)-3.06062\times {10}^{-3}=\left(3.25231\times {10}^{-4}\right)\left(0.88191\right)\\ 52\times {10}^{-6}\left(\Delta T\right)=2.86824\times {10}^{-4}+3.06062\times {10}^{-3}\\ \Delta T=64.4°F\end{array}$

The smallest change in temperature controls the design.

The smallest temperature change occurs when the eccentricity is not considered.

Therefore, the increase in temperature required for the bar to make contact with the point C is $\underset{\_}{58.9°\text{F}}$.