
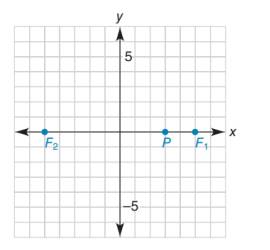
By definition, a hyperbola is the locus of points whose positive difference of distances from two fixed points
Trending nowThis is a popular solution!

Chapter 10 Solutions
Elementary Geometry for College Students
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
College Algebra (Collegiate Math)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Intermediate Algebra (13th Edition)
Graphical Approach To College Algebra
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- MI P X /courses/segura10706/products/171960/pages/611?locale=&platformId=1030&lms=Y ☆ Finish Part I: Mathematics for Elementary and Middle School Teachers Continue in the app JJ 576 Chapter 12. Area of Shapes 9. Determine the area of the shaded shapes in Figure 12.48. Explain your reasoning. 1 unit S Figure 12.48 1 unit unit and the yarn for thearrow_forwardChrom ESS $425 5. Ar Dive for x 21) Name 1. Classify the triangles based on their side lengths and angle measures. 89° 30° Acute Scalene Right Scalene 130° Date A +100 Obtuse Equiangular Isosceles Equilateral What additional information would you need to prove these triangles congruent by ASA? If marrow_forwardBoth find out Only 100% sure experts solve it correct complete solutions okkk don't use chat gpt or other ai okkarrow_forwardOnly 100% sure experts solve it correct complete solutions okkk don't use chat gpt or other ai okkarrow_forwardLogin HAC Home View Summary MwMerriam-Webster: A... Lizard Point Quizze... G Home | Gimkit Quizlet Live | Quizlet K! Kahoot! 7.2 HW Central Angles, Arcs, and Arc Lengths POSSIBLE POINTS: 6.67 11. If myQ=(y+7), mQR = (x+11), mRS = (3y), and mST = 65°, find the values of x and y. R V X = y = W S T q W a It N S C % 65 54 # m d DELL 96 t y 0 27 & J * 00 8 x= y= f g h J k X C V b n 3 ES 1 Feb 26 alt ctrlarrow_forwardThe three right triangles below are similar. The acute angles LL, LR, and ZZ are all approximately measured to be 66.9°. The side lengths for each triangle are as follows. Note that the triangles are not drawn to scale. Z 20.17 m 60.51 m 66.9° 7.92 m 66.9° 80.68 m 66.9° 23.76 m 31.68 m Take one 18.55 m K P 55.65 m X 74.2 m Y (a) For each triangle, find the ratio of the length of the side opposite 66.9° to the length of the hypotenuse. Round your answers to the nearest hundredth. JK JL PQ PR XY ☐ XZ (b) Use the ALEKS Calculator to find sin 66.9°, cos 66.9°, and tan 66.9°. Round your answers to the nearest hundredth. sin 66.9° = ☐ cos 66.9° tan 66.9° = ☐ (c) Which trigonometric function gives each ratio of sides in part (a)? Osine Ocosine Otangent none of thesearrow_forwardT Figure E Statement 33 33° H 40 R 37° 83° S T 55 45 K S 30 U 44 87 H 56 36 ° 54 F 83° 66 P 33 87° ° I 42 200 Rarrow_forwardStella's friends got her a skydiving lesson for her birthday. Her helicopter took off from the skydiving center, ascending in an angle of 37°, and traveled a distance of 2.1 kilometers before she fell in a straight line perpendicular to the ground. How far from the skydiving center did Stella land? Be sure to have all three parts of a CER answer: make a claim, provide evidence, and explain your reasoning for full credit. 2.1 km Landing spot 37% Skydiving centerarrow_forwardIn the graph provided, triangle N'O'P' is the image of triangle NOP after a dilation. 104 -9- -8- 7 6 N 5 0 -4- N 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 p -5 -6 -7 -8 Xarrow_forward104 8 6 4 G G 2 F -10 -8 -6 -4 -2 0 2 4 6 8 10 N H -4 H 6 8 10arrow_forwardThe coordinates of AABC are shown on the coordinate plane provided. AABC is dilated from the origin by scale factor r=2. 2 3 -2 0 1 2 2 m 17arrow_forwardIn the diagram provided, AABC-AAPQ. Read each statement and then arrange the true/false statements in order. B P A Carrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





