9. Find the standard form of the equation of the parabola with a focus at (-3, 4) and directrix y = 2.
9. Find the standard form of the equation of the parabola with a focus at (-3, 4) and directrix y = 2.
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
find the standard form of the equation of the parabola with a focus at -3,4 and directrix at y=2

Transcribed Image Text:The image is of a Cartesian coordinate graph. The graph is a two-dimensional grid marked with both horizontal (x-axis) and vertical (y-axis) lines. Each axis is labeled with numbers ranging from -10 to 10.
- **X-Axis (Horizontal):**
- The center is labeled at 0.
- Positive numbers increase to the right, going up to 10.
- Negative numbers decrease to the left, going down to -10.
- **Y-Axis (Vertical):**
- The center is labeled at 0.
- Positive numbers increase upwards, going up to 10.
- Negative numbers decrease downwards, going down to -10.
The graph consists of a grid made up of smaller squares, which allows for precise plotting of points. Each square represents one unit on both axes. The bold lines at every 5 units help in identifying larger values easily.
![**Problem:**
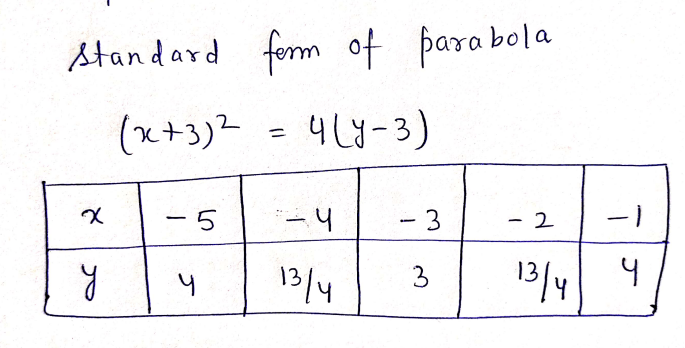
Find the standard form of the equation of the parabola with a focus at (-3, 4) and directrix \( y = 2 \).
**Explanation:**
The problem includes an empty coordinate grid with axes labeled.
To solve the problem, consider the following:
1. **Key points:**
- Focus: \((-3, 4)\)
- Directrix: \(y = 2\)
2. **Determine the Vertex:**
- The vertex of a parabola is equidistant from the focus and the directrix. The distance between the focus and the directrix is \(4 - 2 = 2\).
- Hence, the vertex is 1 unit away from both the focus and the directrix. It lies on the line \(y = 3\) since that’s the midpoint between the focus and the directrix for the y-coordinate. Consequently, the vertex is at \((-3, 3)\).
3. **Equation of the Parabola:**
- Since the parabola opens vertically (upwards due to the focus being above the directrix), use the standard form for vertical parabolas:
\[
(x - h)^2 = 4p(y - k)
\]
where \((h, k)\) is the vertex.
- Here, \(h = -3\) and \(k = 3\).
- The distance \(p\) from the vertex to the focus is 1 (since 4 to 3 is 1 unit).
- Substitute to get the equation:
\[
(x + 3)^2 = 4(y - 3)
\]
This equation can be used to understand the parabola's position and shape with respect to the given focus and directrix.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fda14e668-9ddd-4e75-9b43-53334816616b%2Fb7675a79-199e-4889-a0b4-2f1f7855275f%2Fb2munl_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem:**
Find the standard form of the equation of the parabola with a focus at (-3, 4) and directrix \( y = 2 \).
**Explanation:**
The problem includes an empty coordinate grid with axes labeled.
To solve the problem, consider the following:
1. **Key points:**
- Focus: \((-3, 4)\)
- Directrix: \(y = 2\)
2. **Determine the Vertex:**
- The vertex of a parabola is equidistant from the focus and the directrix. The distance between the focus and the directrix is \(4 - 2 = 2\).
- Hence, the vertex is 1 unit away from both the focus and the directrix. It lies on the line \(y = 3\) since that’s the midpoint between the focus and the directrix for the y-coordinate. Consequently, the vertex is at \((-3, 3)\).
3. **Equation of the Parabola:**
- Since the parabola opens vertically (upwards due to the focus being above the directrix), use the standard form for vertical parabolas:
\[
(x - h)^2 = 4p(y - k)
\]
where \((h, k)\) is the vertex.
- Here, \(h = -3\) and \(k = 3\).
- The distance \(p\) from the vertex to the focus is 1 (since 4 to 3 is 1 unit).
- Substitute to get the equation:
\[
(x + 3)^2 = 4(y - 3)
\]
This equation can be used to understand the parabola's position and shape with respect to the given focus and directrix.
Expert Solution
Step 1

Step 2
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning