Elementary Statistics: A Step By Step Approach
Elementary Statistics: A Step By Step Approach
10th Edition
ISBN: 9781259755330
Author: Allan G. Bluman
Publisher: McGraw-Hill Education
bartleby

Concept explainers

Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as p…
bartleby

Videos

Textbook Question
Book Icon
Chapter 10.1, Problem 1AC

Stopping Distances

In a study on speed control, it was found that the main reasons for regulations were to make traffic flow more efficient and to minimize the risk of danger. An area that was focused on in the study was the distance required to completely stop a vehicle at various speeds. Use the following table to answer the questions.

MPH Braking distance (feet)

20

30

40

50

60

80

20

45

81

133

205

411

Assume MPH is going to be used to predict stopping distance.

1. Which of the two variables is the independent variable?

2. Which is the dependent variable?

3. What type of variable is the independent variable?

4. What type of variable is the dependent variable?

5. Construct a scatter plot for the data.

6. Is there a linear relationship between the two variables?

7. Redraw the scatter plot, and change the distances between the independent-variable numbers. Does the relationship look different?

8. Is the relationship positive or negative?

9. Can braking distance be accurately predicted from MPH?

10.List some other variables that affect braking distance.

11. Compute the value of r.

12. Is r significant at α = 0.05?

1.

Expert Solution
Check Mark
To determine

To identify: The independent variable.

Answer to Problem 1AC

The independent variable is MPH (miles per hour).

Explanation of Solution

Given info:

The table shows the MPH (miles per hour) and Braking distance in feet.

Calculation:

Independent variable:

If the variable does not dependent on the other variables then the variables are said to be independent variable.

Here, the variable “Miles per hour” does not depend on the other variables. Thus, the independent variable is MPH (miles per hour).

2.

Expert Solution
Check Mark
To determine

To identify: The dependent variable.

Answer to Problem 1AC

The dependent variable is Braking distance (feet).

Explanation of Solution

Calculation:

Dependent variable:

If the variable depends on the other variables then the variable is said to be dependent variable.

Here, the variable “Braking distance” depends on the other variables. That is the variable braking distance depends on the MPH (miles per hour). Thus, the dependent variable is Braking distance (feet).

3.

Expert Solution
Check Mark
To determine

The type of variable is the independent variable.

Answer to Problem 1AC

The type of independent variable is the continuous quantitative variable.

Explanation of Solution

Justification:

Continuous quantitative variable:

If the variable takes values on interval scale then the variable is said to be continuous quantitative variable. In the continuous variable, the infinitely many number of values can be considered.

Here, the independent variable miles per hour (MPH) can take any value from a wide range of values. Thus, the independent variable miles per hour (MPH) is continuous quantitative variable.

4.

Expert Solution
Check Mark
To determine

The type of variable is the dependent variable.

Answer to Problem 1AC

The type of dependent variable is the continuous quantitative variable.

Explanation of Solution

Justification:

Here, the dependent variable braking distance (feet) can take any value from a wide range of values. Thus, the independent variable braking distance (feet) is continuous quantitative variable.

5.

Expert Solution
Check Mark
To determine

To construct: The scatterplot for the data.

Answer to Problem 1AC

The scatterplot for the data given data using Minitab software is:

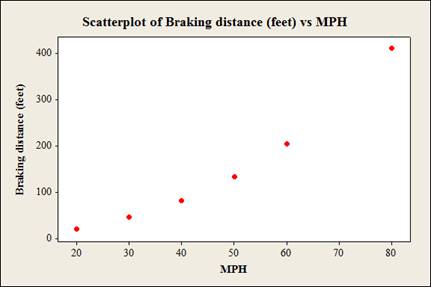
Elementary Statistics: A Step By Step Approach, Chapter 10.1, Problem 1AC , additional homework tip 1

Explanation of Solution

Calculation:

The data shows the MPH (miles per hour) and Braking distance (feet) for vehicles.

Step by step procedure to obtain scatterplot using the MINITAB software:

  • Choose Graph > Scatterplot.
  • Choose Simple and then click OK.
  • Under Y variables, enter a column of Braking distance (feet).
  • Under X variables, enter a column of MPH.
  • Click OK.

6.

Expert Solution
Check Mark
To determine

To check: Whether there is a linear relationship between the two variables.

Answer to Problem 1AC

Yes, there is a linear relationship between the two variables.

Explanation of Solution

Justification:

The horizontal axis represents miles per hour (MPH) and vertical axis represents braking distance (feet).

From the plot, it is observed that there is a linear relationship between the variables miles per hour (MPH) and braking distance (feet) because the data points show a distinct pattern.

7.

Expert Solution
Check Mark
To determine

To construct: The scatterplot for the changed data.

To check: Whether the relationship looks different or not.

Answer to Problem 1AC

The scatterplot for the changed data by using Minitab software is:

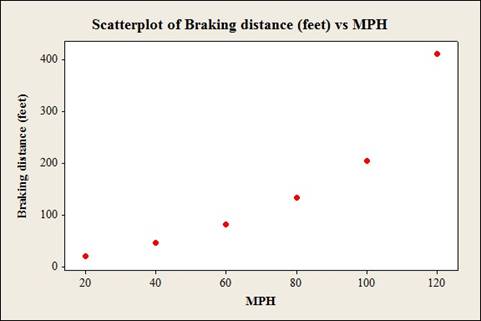
Elementary Statistics: A Step By Step Approach, Chapter 10.1, Problem 1AC , additional homework tip 2

The increments will change the appearance of the relationship if changing the distance between the independent-variable (mph).

Explanation of Solution

Calculation:

The data shows the MPH (miles per hour) and Braking distance (feet) for vehicles.

After changing the distance between the independent-variable numbers, the number of the independent-variable is, 20, 40, 60, 80, 100 and 120.

Step by step procedure to obtain scatterplot using the MINITAB software:

  • Choose Graph > Scatterplot.
  • Choose Simple and then click OK.
  • Under Y variables, enter a column of Braking distance (feet).
  • Under X variables, enter a column of MPH.
  • Click OK.

Justification:

From the graphs it can be observed that, after changing the distance between the independent-variable (mph), the increments will change the appearance of the relationship.

8.

Expert Solution
Check Mark
To determine

To check: Whether the relationship is positive or negative.

Answer to Problem 1AC

The relationship is positive.

Explanation of Solution

Justification:

The relationship is positive because the values of independent variable increases then the values of corresponding dependent variable are increases.

9.

Expert Solution
Check Mark
To determine

To check: Whether the braking distance can be accurately predicted from MPH.

Answer to Problem 1AC

Yes, the braking distance can be accurately predicted from MPH.

Explanation of Solution

Justification:

Here, the braking distance can be accurately predicted from MPH because the relationship between two variables MPH and Breaking distance is strong.

10.

Expert Solution
Check Mark
To determine

To list: The other variables that affect braking distance.

Answer to Problem 1AC

The other variables that affect braking distance are road conditions, driver response time and condition of the brakes.

Explanation of Solution

Justification:

Answer may wary. One of the possible answers is as follows.

The variable affecting the braking distance are road conditions, driver response time and condition of the brakes.

11.

Expert Solution
Check Mark
To determine

To compute: The value of r.

Answer to Problem 1AC

The value of r is 0.966.

Explanation of Solution

Calculation:

Correlation coefficient r:

Software Procedure:

Step-by-step procedure to obtain the ‘correlation coefficient’ using the MINITAB software:

  • Select Stat > Basic Statistics > Correlation.
  • In Variables, select MPH and Braking distance (feet) from the box on the left.
  • Click OK.

Output using the MINITAB software is given below:

Elementary Statistics: A Step By Step Approach, Chapter 10.1, Problem 1AC , additional homework tip 3

Thus, the Pearson correlation of MPH and Braking distance is 0.966.

12.

Expert Solution
Check Mark
To determine

To check: Whether or not the r value is significant at 0.05.

Answer to Problem 1AC

Yes, the r value is significant at 0.05.

Explanation of Solution

Calculation:

Here, the r value is significant is checked. So, the claim is that the r value is significant.

The hypotheses are given below:

Null hypothesis:

H0:ρ=0

That is, there is no linear relation between the MPH and Braking distance.

Alternative hypothesis:

H1:ρ≠0

That is, there is linear relation between the MPH and Braking distance.

The sample size is 6.

The formula to find the degrees of the freedom is n−2 .

That is,

n−2=6−2=4

From the “TABLE –I: Critical Values for the PPMC”, the critical value for 4 degrees of freedom and α=0.05 level of significance is 0.811.

Rejection Rule:

If the absolute value of r is greater than the critical value then reject the null hypothesis.

Conclusion:

From part (11), the Pearson correlation of MPH and Braking distance is 0.966. That is the absolute value of r is 0.966.

Here, |r|>critical value . That is, 0.966>0.811 .

By the rejection rule, reject the null hypothesis.

There is sufficient evidence to support the claim that “there is a linear relation between the MPH and Braking distance”.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Previous
Chapter 9, Problem 25CQ
Next
Chapter 10.1, Problem 1E
Students have asked these similar questions
In order to find probability, you can use this formula in Microsoft Excel: The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest. =NORM.DIST(x, Mean, Standard Dev., TRUE). When the question mentions “greater than” you may have to subtract your answer from 1. When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer. 1.  Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…
If a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9.   The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24?   The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…
Problem 1: The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is: Between the mean and $45 per hour? More than $45 per hour? Less than $32 per hour?   Problem 2: The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds. What is the area between 415 pounds and the mean of 400 pounds? What is the area between the mean and 395 pounds? What is the probability of randomly selecting a value less than 395 pounds?   Problem 3: In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution. What percent of New York State high school teachers earn between 70,000 and 75,000? What percent of New York State high school…

Chapter 10 Solutions

Elementary Statistics: A Step By Step Approach

Ch. 10.1 - Stopping Distances In a study on speed control, it...Ch. 10.1 - What is meant by the statement that two variables...Ch. 10.1 - How is a linear relationship between two variables...Ch. 10.1 - What is the symbol for the sample correlation...Ch. 10.1 - What is the range of values for the correlation...Ch. 10.1 - What is meant when the relationship between the...Ch. 10.1 - Give examples of two variables that are positively...Ch. 10.1 - What is the diagram of the independent and...Ch. 10.1 - What is the name of the correlation coefficient...Ch. 10.1 - What statistical test is used to test the...
Ch. 10.1 - When two variables are correlated, can the...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - Prob. 23ECh. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - For Exercises 11 through 27, perform the following...Ch. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECCh. 10.1 - Prob. 29ECCh. 10.1 - Prob. 30ECCh. 10.2 - Applying the Concepts 102 Stopping Distances...Ch. 10.2 - What two things should be done before one performs...Ch. 10.2 - What are the assumptions for regression analysis?Ch. 10.2 - Prob. 3ECh. 10.2 - What is the symbol for the slope? For the y...Ch. 10.2 - Prob. 5ECh. 10.2 - When all the points fall on the regression line,...Ch. 10.2 - What is the relationship between the sign of the...Ch. 10.2 - As the value of the correlation coefficient...Ch. 10.2 - Prob. 9ECh. 10.2 - When the value of r is not significant, what value...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - Prob. 12ECh. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - Prob. 17ECh. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - For Exercises 11 through 27, use the same data as...Ch. 10.2 - For Exercises 28 through 33, do a complete...Ch. 10.2 - Prob. 29ECh. 10.2 - For Exercises 28 through 33, do a complete...Ch. 10.2 - For Exercises 28 through 33, do a complete...Ch. 10.2 - For Exercises 28 through 33, do a complete...Ch. 10.2 - Prob. 33ECh. 10.2 - For Exercises 34 and 35, do a complete regression...Ch. 10.2 - For Exercises 34 and 35, do a complete regression...Ch. 10.2 - For Exercises 13, 15, and 21 in Section 101, find...Ch. 10.2 - The y intercept value a can also be found by using...Ch. 10.2 - The value of the correlation coefficient can also...Ch. 10.3 - Applying the Concepts 103 Interpreting Simple...Ch. 10.3 - What is meant by the explained variation? How is...Ch. 10.3 - What is meant by the unexplained variation? How is...Ch. 10.3 - What is meant by the total variation? How is it...Ch. 10.3 - Define the coefficient of determination.Ch. 10.3 - How is the coefficient of determination found?Ch. 10.3 - Define the coefficient of nondetermination.Ch. 10.3 - How is the coefficient of nondetermination found?Ch. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Compute the standard error of the estimate for...Ch. 10.3 - Compute the standard error of the estimate for...Ch. 10.3 - Compute the standard error of the estimate for...Ch. 10.3 - Prob. 19ECh. 10.3 - For the data in Exercises 14 in Sections 101 and...Ch. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.4 - Applying the Concepts 104 More Math Means More...Ch. 10.4 - Explain the similarities and differences between...Ch. 10.4 - What is the general form of the multiple...Ch. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - How do the values of the individual correlation...Ch. 10.4 - Age, GPA, and Income A researcher has determined...Ch. 10.4 - Nursing Home Satisfaction A researcher found that...Ch. 10.4 - Special Occasion Cakes A pastry chef who...Ch. 10.4 - Aspects of Students Academic Behavior A college...Ch. 10.4 - Age, Cholesterol, and Sodium A medical researcher...Ch. 10.4 - Explain the meaning of the multiple correlation...Ch. 10.4 - What is the range of values R can assume?Ch. 10.4 - Prob. 13ECh. 10.4 - What are the hypotheses used to test the...Ch. 10.4 - What test is used to test the significance of R?Ch. 10.4 - What is the meaning of the adjusted R2? Why is it...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercises 1 through 7, do a complete...Ch. 10 - For Exercise 4, find the standard error of the...Ch. 10 - Prob. 10.3.9RECh. 10 - Prob. 10.3.10RECh. 10 - Prob. 10.3.11RECh. 10 - Prob. 10.3.12RECh. 10 - (Opt.) A study found a significant relationship...Ch. 10 - Prob. 10.4.14RECh. 10 - Prob. 10.4.15RECh. 10 - Prob. 1CQCh. 10 - Determine whether each statement is true or false....Ch. 10 - Determine whether each statement is true or false....Ch. 10 - Determine whether each statement is true or false....Ch. 10 - Determine whether each statement is true or false....Ch. 10 - Determine whether each statement is true or false....Ch. 10 - Prob. 7CQCh. 10 - Select the best answer. 8. To test the...Ch. 10 - Select the best answer. 9. The test of...Ch. 10 - Prob. 10CQCh. 10 - Prob. 11CQCh. 10 - Prob. 12CQCh. 10 - Complete the following statements with the best...Ch. 10 - Prob. 14CQCh. 10 - Prob. 15CQCh. 10 - Prob. 16CQCh. 10 - Prob. 17CQCh. 10 - Prob. 18CQCh. 10 - Prob. 19CQCh. 10 - Prob. 20CQCh. 10 - Prob. 21CQCh. 10 - Prob. 22CQCh. 10 - Prob. 23CQCh. 10 - For Exercise 20, find the 90% prediction interval...Ch. 10 - Prob. 25CQCh. 10 - Prob. 26CQCh. 10 - (Opt.) Find R when ryx1 = 0.561 and ryx2 = 0.714...Ch. 10 - Prob. 28CQCh. 10 - Prob. 1CTCCh. 10 - Prob. 2CTCCh. 10 - Prob. 3CTCCh. 10 - Prob. 4CTCCh. 10 - Product Sales When the points in a scatter plot...Ch. 10 - Prob. 6CTCCh. 10 - Prob. 7CTCCh. 10 - Product Sales When the points in a scatter plot...Ch. 10 - Prob. 9CTC

Additional Math Textbook Solutions

Find more solutions based on key concepts
Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...

Introductory Statistics

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...

A First Course in Probability (10th Edition)

First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...

Calculus: Early Transcendentals (2nd Edition)

1. How is a sample related to a population?

Elementary Statistics: Picturing the World (7th Edition)

Check Your Understanding Reading Check Complete each sentence using > or < for □. RC1. 3 dm □ 3 dam

Basic College Mathematics

Knowledge Booster
Background pattern image
Statistics
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Correlation Vs Regression: Difference Between them with definition & Comparison Chart; Author: Key Differences;https://www.youtube.com/watch?v=Ou2QGSJVd0U;License: Standard YouTube License, CC-BY
Correlation and Regression: Concepts with Illustrative examples; Author: LEARN & APPLY : Lean and Six Sigma;https://www.youtube.com/watch?v=xTpHD5WLuoA;License: Standard YouTube License, CC-BY