Chapter 10, Problem 10.1.5RE

For Exercises 1 through 7, do a complete regression analysis by performing the following steps.

a. Draw the scatter plot.

b. Compute the value of the correlation coefficient.

c. Test the significance of the correlation coefficient at α = 0.01, using Table I.

d. Determine the regression line equation if r is significant.

e. Plot the regression line on the scatter plot, if appropriate.

f. Predict y′ for a specific value of x, if appropriate.

5. Typing Speed and Word Processing A researcher desires to know whether the typing speed of a secretary (in words per minute) is related to the time (in hours) that it takes the secretary to learn to use a new word processing program. The data are shown.

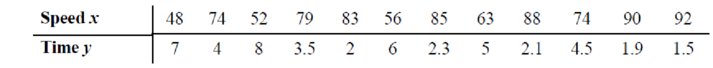
If there is a significant relationship, predict the time it will take the average secretary who has a typing speed of 72 words per minute to learn the word processing program. (This information will be used for Exercises 9 and 11.)

To determine

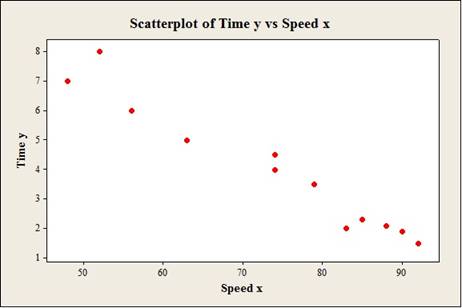
To construct: The scatterplot for the variablesthe speed and time.

Answer to Problem 10.1.5RE

Output using the MINITAB software is given below:

Explanation of Solution

Given info:

The data shows the typing speed of a secretary (in words per minute) (x) and the time (in hours) (y) values.

Calculation:

Step by step procedure to obtain scatterplot using the MINITAB software:

• Choose Graph > Scatterplot.
• Choose Simple and then click OK.
• Under Y variables, enter a column ofTime.
• Under X variables, enter a column ofSpeed.
• Click OK.

To determine

To compute: The value of the correlation coefficient.

Answer to Problem 10.1.5RE

The value of the correlation coefficientis –0.974.

Explanation of Solution

Calculation:

Correlation coefficient r:

Software Procedure:

Step-by-step procedure to obtain the ‘correlation coefficient’ using the MINITAB software:

• Select Stat >Basic Statistics > Correlation.
• In Variables, select x and y from the box on the left.
• Click OK.

Output using the MINITAB software is given below:

From the MINITAB output, the value of the correlation is –0.974.

To determine

To test: The significance of the correlation coefficient at $\alpha =0.01$ using Table I.

Answer to Problem 10.1.5RE

The conclusion is that,there is a linear relation between the speed and time.

Explanation of Solution

Given info:

The level of significance is $\alpha =0.01$ and the sample size is 12.

Calculation:

The hypotheses are given below:

Null hypothesis:

$H_0:\rho =0$

That is, there is no linear relation betweenthe speed and time.

Alternative hypothesis:

$H_1:\rho \ne 0$

That is, there is a linear relation between the speed and time.

The sample size is 12.

The formula to find the degrees of the freedom is $n-2$.

That is,

$\begin{array}{c}n-2=12-2\\ =10\end{array}$

From the “TABLE –I: Critical Values for the PPMC”, the critical value for 10 degrees of freedom and $\alpha =0.01$ level of significance is 0.708.

Rejection Rule:

If the absolute value of r is greater than the critical value then reject the null hypothesis.

Conclusion:

From part (b), the value of r is–0.974that is the absolute value of r is 0.974.

Here, the absolute value of r is greater than the critical value $\left|r\right|>\text{critical value}$.

That is, $\left|r\right|\left(=0.974\right)<\text{critical value}\left(=0.708\right)$.

By the rejection rule,reject the null hypothesis.

There is asufficient evidence to support the claim that “there is alinear relation betweenthespeed and time.

To determine

To find: The regression equation for the given data.

Answer to Problem 10.1.5RE

The regression equation for the given datais $\widehat{y}=14.086-0.137x$.

Explanation of Solution

Calculation:

Regression:

Software procedure:

Step by step procedure to obtain the regression equation using the MINITAB software:

• Choose Stat > Regression > Regression.
• In Responses, enter the column ofTime.
• In Predictors, enter the column ofSpeed.
• Click OK.

Output using the MINITAB software is given below:

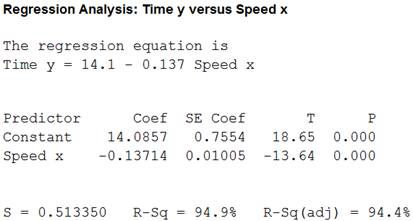
Thus, regression equation for the given datais $\widehat{y}=14.086-0.137x$.

To determine

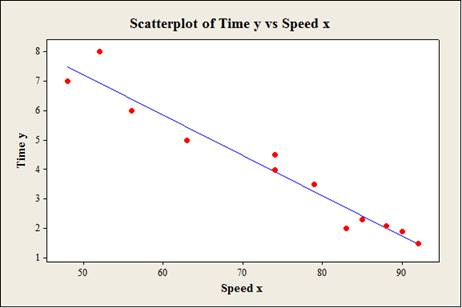
To construct: The scatterplot for the variablesthe speed and time with regression line.

Answer to Problem 10.1.5RE

Output using the MINITAB software is given below:

Explanation of Solution

Calculation:

Step by step procedure to obtain scatterplot using the MINITAB software:

• Choose Graph > Scatterplot.
• Choose with line and then click OK.
• Under Y variables, enter a column of Time.
• Under X variables, enter a column ofSpeed.
• Click OK.

To determine

To obtain: The predicted value of the time with speed of 72 words perminute.

Answer to Problem 10.1.5RE

Thepredicted value of the time is 4.726.

Explanation of Solution

Calculation:

Thus, regression equation for the given datais $\widehat{y}=14.086-0.137x$.

Substitute x as 72 in the regression equation

$\begin{array}{c}\widehat{y}=14.086-0.137x\\ =14.086-\left(0.137\times 72\right)\\ =14.086-9.36\\ =4.726\end{array}$

Thus, the predicted value of the time is 4.726.