EBK PHYSICS FOR SCIENTISTS & ENGINEERS
5th Edition
ISBN: 9780134296074
Author: GIANCOLI
Publisher: VST
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10, Problem 39P
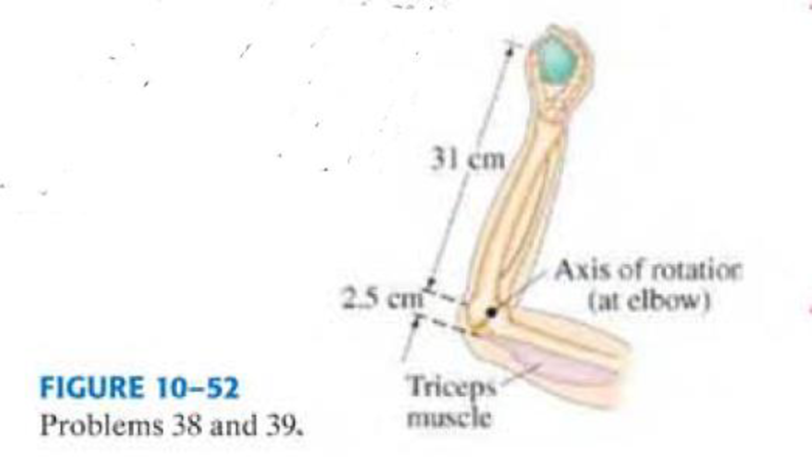
(II) Assume that a 1.00-kg ball is thrown solely by the action of the forearm, which rotates about the elbow joint under the action of the triceps muscle, Fig. 10–52. The ball is accelerated uniformly from rest to 8.5 m/s in 0.35 s, at which point it is released. Calculate (a) the
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
. (II) Assume that a 1.00-kg ball is thrown solely by the action of the forearm, which rotates about the elbow joint under the actionof the triceps muscle, Fig. 8–46. The ball is accelerated uniformlyfrom rest to 8.5 m/s in 0.38 s, at which point it is released. Calculate (a) the angular acceleration of the arm, and (b) the force required of the triceps muscle. Assume that the forearm has a mass of 3.7 kg and rotates like a uniform rod about an axis at its end.
(II) A potter is shaping a bowl on a potter's wheel rotating at
constant angular velocity of 1.6 rev/s (Fig. 8–48). The friction
force between her hands and the clay is 1.5 N total. (a) How
large is her torque on the wheel, if the diameter of the bowl
is 9.0 cm? (b) How long would it take for the potter's wheel
to stop if the only torque acting on it is due to the potter's
hands? The moment of inertia of the wheel and the bowl is
0.11 kg•m².
FIGURE 8–48
Problem 40.
A small mass m on a string is rotating without friction in acircle. The string is shortened by pulling it through the axisof rotation without any external torque, Fig. 8–39. Whathappens to the tangential velocity of the object?(a) It increases.(b) It decreases.(c) It remains the same.
Chapter 10 Solutions
EBK PHYSICS FOR SCIENTISTS & ENGINEERS
Ch. 10.1 - In Example 103, we found that the carousel, after...Ch. 10.4 - Two forces (FB = 20 N and FA = 30 N) are applied...Ch. 10.7 - In Figs. 1020f and g, the moments of inertia for a...Ch. 10.8 - Estimate the energy stored in the rotational...Ch. 10.9 - Return to the Chapter-Opening Question, p. 248,...Ch. 10.9 - Find the acceleration a of a yo-yo whose spindle...Ch. 10 - Prob. 1QCh. 10 - Suppose a disk rotates at constant angular...Ch. 10 - Could a nonrigid object be described by a single...Ch. 10 - Prob. 4Q
Ch. 10 - Prob. 5QCh. 10 - Prob. 6QCh. 10 - Can a small force ever exert a greater torque than...Ch. 10 - Why is it more difficult to do a sit-up with your...Ch. 10 - If the net force on a system is zero, is the net...Ch. 10 - Mammals that depend on being able to run fast have...Ch. 10 - Prob. 11QCh. 10 - Prob. 12QCh. 10 - Prob. 13QCh. 10 - Prob. 14QCh. 10 - Two inclines have the same height but make...Ch. 10 - Two spheres look identical and have the same mass....Ch. 10 - A sphere and a cylinder have the same radius and...Ch. 10 - Two solid spheres simultaneously start rolling...Ch. 10 - Prob. 1MCQCh. 10 - Prob. 2MCQCh. 10 - Prob. 3MCQCh. 10 - Prob. 4MCQCh. 10 - Prob. 6MCQCh. 10 - Prob. 7MCQCh. 10 - Prob. 8MCQCh. 10 - Prob. 9MCQCh. 10 - Prob. 10MCQCh. 10 - Prob. 11MCQCh. 10 - Prob. 12MCQCh. 10 - Prob. 14MCQCh. 10 - (I) Express the following angles in radians: (a)...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - (I) The blades in a blender rotate at a rate of...Ch. 10 - Prob. 5PCh. 10 - Prob. 6PCh. 10 - Prob. 7PCh. 10 - Prob. 8PCh. 10 - Prob. 9PCh. 10 - (II) A rotating merry-go-round makes one complete...Ch. 10 - Prob. 11PCh. 10 - Prob. 12PCh. 10 - (II) Calculate the angular velocity of the Earth...Ch. 10 - Prob. 14PCh. 10 - Prob. 15PCh. 10 - Prob. 16PCh. 10 - (II) A turntable of radius R1 is turned by a...Ch. 10 - Prob. 18PCh. 10 - (I) A centrifuge accelerates uniformly front rest...Ch. 10 - Prob. 20PCh. 10 - Prob. 21PCh. 10 - Prob. 22PCh. 10 - Prob. 23PCh. 10 - Prob. 24PCh. 10 - Prob. 25PCh. 10 - Prob. 26PCh. 10 - Prob. 27PCh. 10 - (II) Two blocks, each of mass m, are attached to...Ch. 10 - Prob. 29PCh. 10 - Prob. 30PCh. 10 - Prob. 31PCh. 10 - Prob. 32PCh. 10 - Prob. 33PCh. 10 - (I) Estimate the moment of inertia of a bicycle...Ch. 10 - Prob. 35PCh. 10 - (II) An oxygen molecule consists of two oxygen...Ch. 10 - Prob. 37PCh. 10 - (II) The forearm in Fig. 1052 accelerates a 3.6-kg...Ch. 10 - (II) Assume that a 1.00-kg ball is thrown solely...Ch. 10 - Prob. 40PCh. 10 - Prob. 41PCh. 10 - Prob. 42PCh. 10 - Prob. 43PCh. 10 - (II) A dad pushes tangentially on a small...Ch. 10 - Prob. 45PCh. 10 - Prob. 46PCh. 10 - Prob. 47PCh. 10 - Prob. 48PCh. 10 - (II) When discussing moments of inertia,...Ch. 10 - (II) Two blocks are connected by a light string...Ch. 10 - Prob. 51PCh. 10 - (III) A hammer thrower accelerates the hammer...Ch. 10 - (I) Use the parallel-axis theorem to show that the...Ch. 10 - (II) Determine the moment of inertia of a 19-kg...Ch. 10 - Prob. 55PCh. 10 - Prob. 56PCh. 10 - Prob. 57PCh. 10 - Prob. 58PCh. 10 - Prob. 61PCh. 10 - Prob. 62PCh. 10 - (I) Estimate the kinetic energy of the Earth with...Ch. 10 - (II) A rotating uniform cylindrical platform of...Ch. 10 - Prob. 65PCh. 10 - (II) A Uniform thin rod of length l and mass M is...Ch. 10 - Prob. 67PCh. 10 - (III) A 2.30-m-long pole is balanced vertically on...Ch. 10 - Prob. 69PCh. 10 - (I) A bowling ball of mass 7.3kg and radius 9.0 cm...Ch. 10 - Prob. 71PCh. 10 - (II) A narrow but solid spool of thread has radius...Ch. 10 - (II) A solid rubber ball rests on the floor of a...Ch. 10 - Prob. 74PCh. 10 - Prob. 75PCh. 10 - (II) A ball of radius r0 rolls on the inside of a...Ch. 10 - (III) A small sphere of radius r0 = 1.5 cm rolls...Ch. 10 - (III) A wheel with rotational inertia I=12MR2...Ch. 10 - (III) The 1100-kg mass of a car includes four...Ch. 10 - (I) A rolling hall slows down because the normal...Ch. 10 - Prob. 81GPCh. 10 - On a 12.0-cm-diameter audio compact disc (CD),...Ch. 10 - (a) A yo-yo is made of two solid cylindrical...Ch. 10 - Prob. 84GPCh. 10 - Prob. 85GPCh. 10 - A large spool of rope rolls on the ground with the...Ch. 10 - Bicycle gears: (a) How is the angular velocity R...Ch. 10 - Prob. 88GPCh. 10 - Figure 1065 illustrates an H2O molecule. The O H...Ch. 10 - Prob. 90GPCh. 10 - Prob. 91GPCh. 10 - Prob. 92GPCh. 10 - Prob. 93GPCh. 10 - Prob. 94GPCh. 10 - Prob. 96GPCh. 10 - A marble of mass m and radius r rolls along the...Ch. 10 - The density (mass per unit length) of a thin rod...Ch. 10 - If a billiard ball is hit in just the right way by...Ch. 10 - Prob. 100GPCh. 10 - When bicycle and motorcycle riders pop a wheelie,...Ch. 10 - A crucial part of a piece of machinery starts as a...Ch. 10 - Prob. 103GPCh. 10 - Prob. 104GPCh. 10 - Prob. 105GPCh. 10 - A thin uniform stick of mass M and length l is...Ch. 10 - Prob. 107GP
Additional Science Textbook Solutions
Find more solutions based on key concepts
34. The free-fall acceleration at the surface of planet 1 is 20 m/s2. The radius and the mass of planet 2 are t...
College Physics: A Strategic Approach (3rd Edition)
Why would it be impossible for organisms to grow at 200 or 300C?
Brock Biology of Microorganisms (15th Edition)
Q1. What is the empirical formula of a compound with the molecular formula
Chemistry: A Molecular Approach (4th Edition)
Which one of the following is not a fuel produced by microorganisms? a. algal oil b. ethanol c. hydrogen d. met...
Microbiology: An Introduction
1. How many significant figures does each of the following numbers have?
a. 0.73 b. 7.30 c. 73 d. 0.073
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Explain all answers clearly, with complete sentences and proper essay structure if needed. An asterisk (*) desi...
Cosmic Perspective Fundamentals
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- (II) Two masses, mA = 35.0 kg and mB = 38.0 kg, are connected by a rope that hangs over a pulley (as in Fig. 10-59). The pulley is a uniform cylinder of radius 0.381 m and mass 3.1 kg. Initially ma is on the ground and mB rests 2.5 m above the ground. If the system is released, use conservation of energy to deter- mine the speed of mB just before it strikes the ground. Assume the pulley bearing is frictionless. %3D RO mB mA 2.5 m FIGURE 10-59 ba Problem 67. inoni lo (IID) A.arrow_forward(II) A rotating uniform cylindrical platform of mass 220 kg and radius 5.5 m slows down from 3.8 rev/s to rest in 16 s when the driving motor is disconnected. Estimate the power output of the motor (hp) required to maintain a steady speed of 3.8 rev/s.arrow_forward(II) A small rubber wheel is used to drive a large potterywheel. The two wheels are mounted so that their circularedges touch. The small wheel has a radius of 2.0 cm andaccelerates at the rate of 7.2 rad/s and it is in contact withthe pottery wheel (radius 27.0 cm) without slipping. Calculate (a) the angular acceleration of the pottery wheel, and(b) the time it takes the pottery wheel to reach its requiredspeed of 65 rpmarrow_forward
- (II) A nonrotating cylindrical disk of moment of inertia I is dropped onto an identical disk rotating at angular speed w. Assuming no external torques, what is the final common angular speed of the two disks?arrow_forwardA 4.00-kg mass and a 3.00-kg mass are attached to opposite ends of a very light 42.0-cm-long horizontal rod (Fig. 8–61). The system is rotating at angular speed w = 5.60 rad/s about a vertical axle at the center of the rod. Determine (a) the kinetic energy KE of the system, and (b) the net force on each mass. 3.00 kg 4.00 kg FIGURE 8-61 Problem 87.arrow_forwardA 4.00-kg mass and a 3.00-kg mass are attached to opposite ends of a very light 42.0-cm-long horizontal rod (Fig. 8–61). The system is rotating at angular speed v = 5.60 rad/s about a vertical axle at the center of the rod. Determine (a) the kinetic energy KE of the system, and (b) the net force on each mass.arrow_forward
- (I) Calculate the translational speed of a cylinder when itreaches the foot of an incline 7.20 m high. Assume it startsfrom rest and rolls without slippingarrow_forward(II) A cooling fan is turned off when it is running at 850 rev/minIt turns 1250 revolutions before it comes to a stop. (a) What was the fan’s angular acceleration, assumedconstant? (b) How long did it take the fan to come to acomplete stop?arrow_forward(III) Suppose a 65-kg person stands at the edge of a 5.5-mdiameter merry-go-round turntable that is mounted onfrictionless bearings and has a moment of inertia of 1850 kg.m2The turntable is at rest initially, but when theperson begins running at a speed of 4.0 m/s (with respectto the turntable) around its edge, the turntable begins torotate in the opposite direction. Calculate the angularvelocity of the turntable.arrow_forward
- (III) An Atwood machine consists of two masses, ma = 65 kg and mg = 75 kg, connected by a massless inelastic cord that passes over a pulley free to rotate, Fig. 8–52. The pulley is a solid cylin- der of radius R = 0.45 m and mass 6.0 kg. (a) Determine the accelera- tion of each mass. (b) What % error would be made if the moment of ROR inertia of the pulley is ignored? [Hint: The tensions FTA and FrB are not equal. We discussed the Atwood machine in Example 4–13, assuming I = 0 for the pulley.] FTA TB FIGURE 8–52 Problem 47. MB Atwood machine.arrow_forward(II) A small 350-gram ball on the end of a thin, light rodis rotated in a horizontal circle of radius 1.2 m. Calculate(a) the moment of inertia of the ball about the center ofthe circle, and (b) the torque needed to keep the ballrotating at constant angular velocity if air resistance exertsa force of 0.020 N on the ball. Ignore air resistance onthe rod and its moment of inertia.arrow_forward(II) A wheel of diameter 27.0 cm is constrained to rotate in the xy plane, about the z axis, which passes through its center. A force F = (-31.0i + 43.4j) N acts at a' point on the edge of the wheel that lies exactly on the x axis at a particular instant. What is the torque about the rotation axis at this instant?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Rotational Kinetic Energy; Author: AK LECTURES;https://www.youtube.com/watch?v=s5P3DGdyimI;License: Standard YouTube License, CC-BY