
Concept explainers
a)
To determine: The mean of each sample.
a)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean of each sample:
| Sample | ||||
| Sl. No. | 1 | 2 | 3 | 4 |
| 1 | 4.5 | 4.6 | 4.5 | 4.7 |
| 2 | 4.2 | 4.5 | 4.6 | 4.6 |
| 3 | 4.2 | 4.4 | 4.4 | 4.8 |
| 4 | 4.3 | 4.7 | 4.4 | 4.5 |
| 5 | 4.3 | 4.3 | 4.6 | 4.9 |
| Mean | 4.3 | 4.5 | 4.5 | 4.7 |
Table 1
Excel Worksheet:
Sample 1:
The mean is calculated by adding each sample points. Adding the points 4.5, 4.2, 4.2, 4.3 and 4.3 and dividing by 5 gives mean of 4.3. The same process is followed for finding mean for other samples.
Hence, the mean of each sample is shown in Table 1
b)
To determine: The mean and standard deviation when the process parameters are unknown.
b)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean and standard deviation:
Table 1 provides the mean for each sample points.
The mean is calculated by adding each mean of the samples. Adding the points 4.3, 4.5, 4.5 and 4.7 and dividing by 4 gives mean of 4.5.
The standard deviation is calculated using the above formula and substituting the values of mean in the above formula and the resultant of 0.192 is obtained.
Hence, the mean and standard deviation when the process parameters are unknown are 4.5 and 0.192.
c)
To determine: The mean and standard deviation of the sampling distribution.
c)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean and standard deviation of the sampling distribution:
From calculation of mean of each samples, the mean for sampling distribution can be computed, the mean for sampling distribution is 4.5 (refer equation (1)).
The standard deviation of the sampling distribution is calculated by dividing 0.192 with the square root of 5 which gives the resultant as 0.086.
Hence, the mean and standard deviation of the sampling distribution is 4.5 and 0.086 respectively.
d)
To determine: The three-sigma control limit for the process and alpha risk provided by them.
d)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of three-sigma control limit for the process:
The three-sigma control limits for the process is calculated by multiplying 3.00 with 0.086 (refer equation (2)) and the resultant is added with 4.5 to get an upper control limit which is 4.758 and subtracted to get lower control limit which is 4.242. Using z-factor table z = +3.00 corresponds to 0.4987.
The alpha risk is calculated to be as 0.0026.
Hence, the three-sigma control limits for the process are 4.758 and 4.242.
e)
To determine: The alpha risk for control limits of 4.14 and 4.86.
e)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Formula:
Calculation alpha risk for control limits of 4.14 and 4.86:
The alpha risk is calculated by dividing the difference of 4.86 and 4.5 with 0.086 which gives +4.19 which is the risk is close to zero.
Hence, the alpha risk for control limits of 4.14 and 4.86 is +4.1
f)
To determine: Whether any of the sample means are beyond the control limits.
f)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Determination of whether any of the sample means are beyond the control limits:
Table 1 provides the sample means for each sample. From observation, it can be found that each sample mean are within the control limit of 4.14 and 4.86. Therefore, each sample means lies within the control limits of 4.14 and 4.86.
Hence, there are no sample means which lies beyond the control limits.
g)
To determine: Whether any of the samples are beyond the control limits.
g)
Answer to Problem 20P
Explanation of Solution
Given information:
| SAMPLE | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Formula:
Mean Chart:
Range Chart:
Calculation of upper and lower control limits:
| SAMPLE | ||||
| 1 | 2 | 3 | 4 | |
| 4.5 | 4.6 | 4.5 | 4.7 | |
| 4.2 | 4.5 | 4.6 | 4.6 | |
| 4.2 | 4.4 | 4.4 | 4.8 | |
| 4.3 | 4.7 | 4.4 | 4.5 | |
| 4.3 | 4.3 | 4.6 | 4.9 | |
| Mean | 4.3 | 4.5 | 4.5 | 4.7 |
| Range | .3 | .4 | .2 | .4 |
From factors of three-sigma chart, A2 = 0.58; D3 = 0; D4 = 2.11.
Mean control chart:
Upper control limit:
The Upper control limit is calculated by adding the product of 0.58 and 0.325 with 4.5 which yields 4.689.
Lower control limit:
The Lower control limit is calculated by subtracting the product of 0.58 and 0.325 with 4.5 which yields 4.311.
The UCL and LCL for mean charts are 4.686 and 4.311. (4)
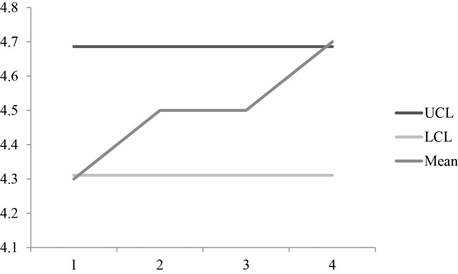
A graph is plotted using the UCL and LCL and mean values which shows the points are within the control limits.
Range control chart:
Upper control limit:
The Upper control limit is calculated by multiplying 2.11 with 0.325 which yields 0.686.
Lower control limit:
The lower control limit is calculated by multiplying 0 with 0.325 which yields 0.0.
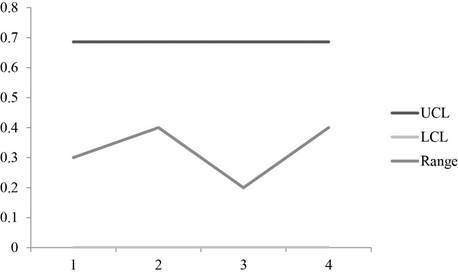
A graph is plotted using the UCL, LCL and Range values which shows that the points are within the control region.
Hence, all points are within control limits.
h)
To explain: The reason for variations in control limits.
h)
Answer to Problem 20P
Explanation of Solution
Reason for variations in control limits:
The control limits vary because in equation (3) and (4) because of the use of different measure for dispersion to measure the standard deviation and range.
Hence, the difference arises due to the use of different measures for dispersion to the measure the standard deviation and range.
i)
To determine: The control limits for the process and whether the process will be in control.
i)
Answer to Problem 20P
Explanation of Solution
Given information:
Determination of control limits of the process:
Sample mean is given in Table 1.
To calculate the control limits 0.18 is divided by root of 5 and is multiplied by 3 and the resultant is added to 4.4 to give UCL which is 4.641 and subtracted from 4.4 to get the LCL which is 4.159.
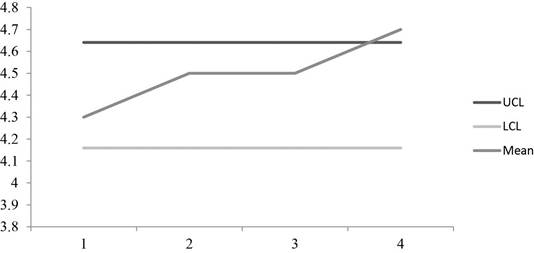
The graph shows that the some of the points are above the control limits which make the process to be out of control.
Hence, the process is out of control with UCL=4.641 and LCL=4.159.
Want to see more full solutions like this?
Chapter 10 Solutions
EBK OPERATIONS MANAGEMENT
- How can HR proactively help ensure that other departments are operating in a legally acceptable manner? Answers Deliver interdepartmental training on legal compliance and requirements. Discuss potential sources of risk with an attorney and create a plan to respond to lawsuits. Ensure that all HR members are watching the conduct of other departments and report infractions to the head of HR. Record improper conduct from various employees throughout the organization and pursue disciplinary measures.arrow_forwardCan you guys help me with this? Thank you! Project is Terminal 1 at JFK International Airport Question: Risk management content: Discuss a major risk management event that affected the project (Keep this content about 2 minute talking and please provide actual sources that you have the information to go over this)arrow_forwarduse the screenshot to find the anwser to this If the project finishes within 27 weeks of its start, the project manager receives a $500 bonus. What is the probability of a $500 bonus? Note: Round z-value to 2 decimal places, and probability to 4 decimal places.arrow_forward
- Scan To Pay Log into your own Lightning UPI account of supporting app and scan QR code below to pay! ✰ BINANCEarrow_forwardTo help with preparations, a couple has devised a project network to describe the activities that must be completed by their wedding date. Start A Ꭰ F B E The following table lists the activity time estimates (in weeks) for each activity. Optimistic Most Probable Activity Pessimistic A 4 5 6 B 2.5 3 3.5 C 5 6 7 D 5 5.5 9 E 5 7 9 F 2 3 4 G 7 9 11 H 5 6 13 H Finish Based only on the critical path, what is the estimated probability that the project will be completed within the given time frame? (Round your answers to four decimal places.) (a) Within 19 weeks? (b) Within 21 weeks? (c) Within 25 weeks?arrow_forwardYou may need to use the appropriate technology to answer this question. Mueller Associates is a urban planning firm that is designing a new public park in an Omaha suburb. Coordination of the architect and subcontractors will require a major effort to meet the 46-week completion date requested by the owner. The Mueller project manager prepared the following project network. B H Start A C G Finish E Estimates of the optimistic, most probable, and pessimistic times (in weeks) for the activities are as follows. Activity Optimistic Most Probable Pessimistic A 4 12 B 6 7 8 C 6 18 D 3 5 7 E 6 9 18 F 5 8 17 G 10 15 20 H 5 13 (a) Find the critical path. (Enter your answers as a comma-separated list.) (b) What is the expected project completion time (in weeks)? weeks i (c) Based only on the critical path, what is the estimated probability the project can be completed in 46 weeks as requested by the owner? (Round your answer to four decimal places.) (d) Based only on the critical path, what is…arrow_forward
- Bridge City Developers is coordinating the construction of an office complex. As part of the planning process, the company generated the following activity list. Draw a project network that can be used to assist in the scheduling of the project activities. Activity Immediate Predecessor ABC E FGH ] A, B A, B D E с с F, G, H, I A E Start B D A E Start B D H H E A E Finish Start D F J Finish Start B D F Finish Finish C H I Harrow_forwardHow can mindfulness be combined with cognitive reframing to build emotional regulation and mental flexibility? What is the strategy for maintaining mental well-being to improve through deliberate practice? How to engage in practices that help regulate emotions and build resilience?arrow_forward• We Are HIRING Salesforce Developer (2 - 4 Years) @ Cloudodyssey It Solutions Requirement : Appropriate knowledge on Salesforce standard objects Leads, Account, Contacts, Opportunity, Products, Lead process, Sales process, is required. • Hands-on experience in Salesforce Experience Cloud, Sales Cloud and Lightning. • • Hands experience with Salesforce development, administration, system integrations, Lightning Design System, and bug fixes. Experience in configuration, integration, APIs creation, testing and deployment of Salesforce.com functionality. Eloquent verbal and written communication skills. • Familiar with Agile framework. Work Location: Bangalore SUBMIT YOUR CV hello@cloudodyssey.coarrow_forward
- Agree or disagree with post On the surface, the numbers in financial statements do present a snapshot of a company's financial position and performance. However, just looking at the raw numbers often doesn't tell the whole story or reveal underlying trends and relationships that are crucial for making informed decisions. Think of it like looking at individual pieces of a puzzle. Each number is a piece, providing some information. But to see the complete picture – the company's overall financial health, its performance over time, how it compares to its peers, and its potential future – you need to assemble those pieces using different analytical tools. For example: Horizontal analysis helps us understand how specific financial statement items have changed over multiple periods. Is revenue growing? Are expenses increasing at a faster rate than sales? This reveals trends that a single year's numbers wouldn't show. Vertical analysis allows us to see the relative size of each item within…arrow_forwardWhat can you do in response to an insulting offer?arrow_forwardAgree or disagree with post If someone hits you with an insulting offer, the first thing to do is not take it personally. It’s normal to feel a little offended, but blowing up or shutting down won’t help your case. Better move is to stay calm and treat it like a misunderstanding or just the first step in the conversation. That way, you keep things respectful but still let them know the offer doesn’t sit right with you. It also helps to back up your response with facts. Bring in things like your experience, numbers, or any specific results you delivered. That can shift the conversation away from feelings and toward the value you bring. Agree or disagree with postarrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

