
Concept explainers
 ICA 10-5
ICA 10-5
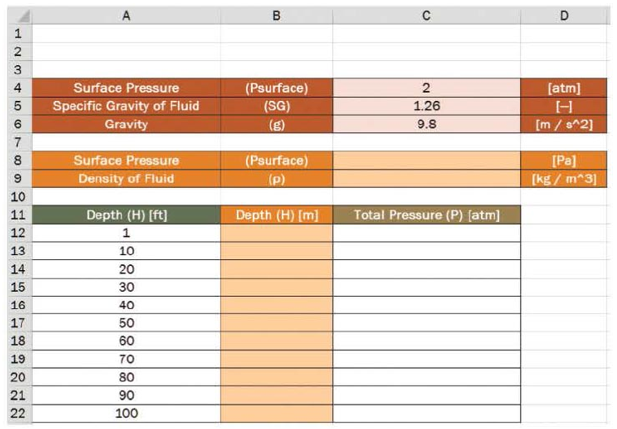
The worksheet shown here was designed to calculate the total pressure felt by an object submerged in a fluid as a function of the depth to which the object is submerged. The user will enter the surface pressure (in units of atmospheres), specific gravity of the fluid, and the gravity of the planet (in units of meters per second squared). All user input is shown in red. The worksheet will calculate the surface pressure in units of pascals, the density of the fluid in kilograms per cubic meter, and depth in units of feet. All conversions are shown in orange. Finally, the worksheet will calculate the total pressure in units of atmospheres.
- a. What formula should be typed in cell C8 to convert the surface pressure in cell C4 from atmospheres to pascals?
- b. What formula should be typed in cell C9 to determine the density in units of kilograms per cubic meter?
- c. What formula should be typed into cell B12 that can then be copied clown column B to convert the depth from units of feet to units of meters?
- d. What formula should be typed into cell C12 that can then be copied down column C to calculate the total pressure in units of atmospheres?
a.
Write the formula to be entered in cell C8 to convert the atmospheres surface pressure entered in cell C4 to Pascal.
Answer to Problem 1ICA
The formula to be entered in cell C8 to convert the atmospheres surface pressure entered in cell C4 to Pascal is “
Explanation of Solution
Given data:
The worksheet is given as follows.
Calculation:
Consider the conversion factor for atmospheres to Pascal.
Step 1:
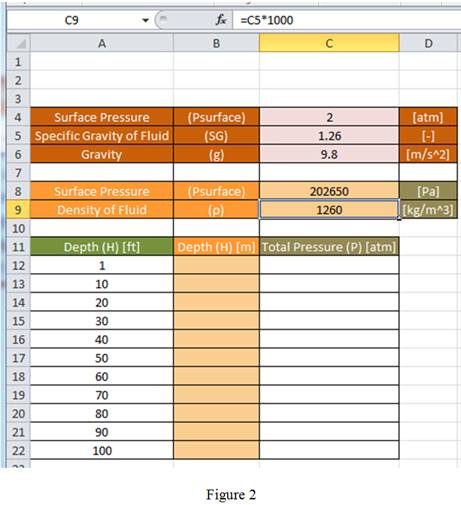
Using equation (1), enter the formula “

Conclusion:
Hence, the formula to be entered in cell C8 to convert the atmospheres surface pressure entered in cell C4 to Pascal is “
b.
Write the formula to be entered in cell C9 to determine the density in units of kilograms per cubic meter.
Answer to Problem 1ICA
The formula to be entered in cell C9 to determine the density in units of kilograms per cubic meter is “
Explanation of Solution
Calculation:
Write the expression for density.
Step 1:
Using equation (2), enter the formula “
Conclusion:
Hence, the formula to be entered in cell C9 to determine the density in units of kilograms per cubic meter is “
c.
Write the formula to be entered in cell B12 that can be then be copied down column B to convert the depth in feet to meters.
Answer to Problem 1ICA
The formula to be entered in cell B12 that can be then be copied down column B to convert the depth in feet to meters is “
Explanation of Solution
Calculation:
Write the conversion factor for feet to meter.
Step 1:
Using equation (3), enter the formula “
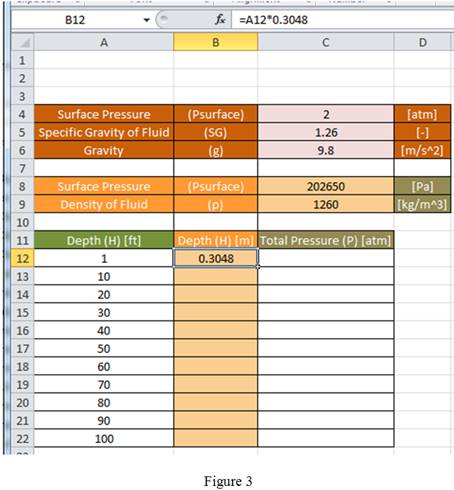
Drag the same formula for remaining cells in the column to obtain the value of depth in terms of m as shown in Figure 4.
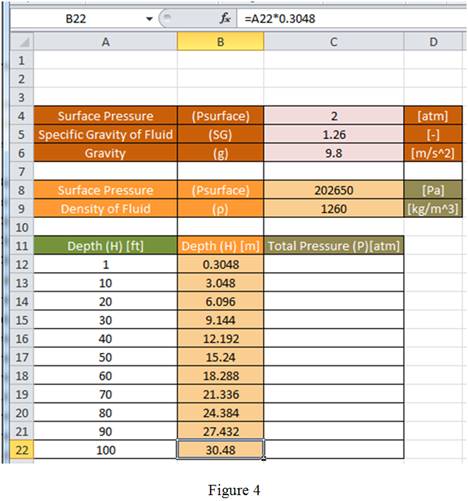
Conclusion:
Hence, the formula to be entered in cell B12 that can be then be copied down column B to convert the depth in feet to meters is “
d.
Write the formula to be entered in cell C12 that can be then be copied down column C to calculate the total pressure in atmospheres.
Answer to Problem 1ICA
The formula to be entered in cell C12 that can be then be copied down column C to calculate the total pressure in atmospheres is “
Explanation of Solution
Calculation:
Write the expression for total pressure.
Re-arrange equation (1) as follows.
Step 1:
Since, the content of cell C8 is in Pascal, the result obtained for total pressure using cell C8, C9, C6 and B12 is divided by 101,325 to convert the result from Pascal to atmosphere.
Using equation (4) and (5), enter the formula “
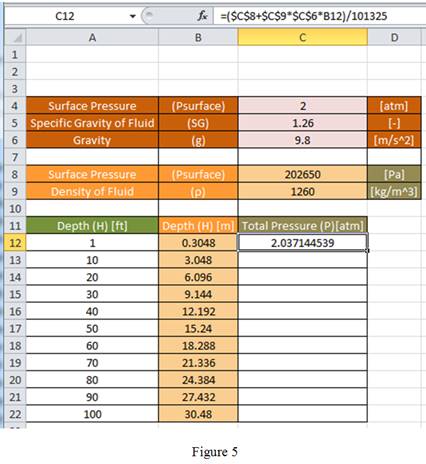
Drag the same formula for remaining cells in the column to obtain the total pressure value as shown in Figure 6.
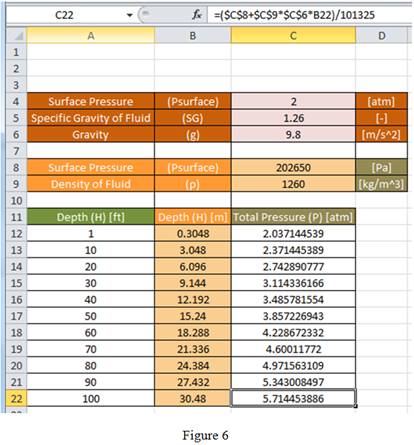
Since, the content of cell C4 is in atmosphere, the result obtained for
Using equation (4) and (5), enter the formula “
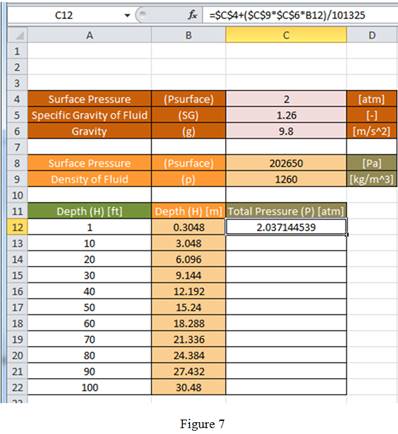
Drag the same formula for remaining cells in the column to obtain the total pressure value as shown in Figure 8.
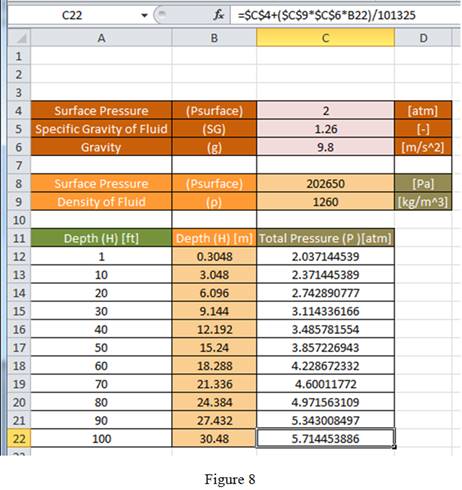
Compare Figure 5 with Figure 7 and Figure 6 with Figure 8, the result obtained for total pressure using formula
Conclusion:
Hence, the formula to be entered in cell C12 that can be then be copied down column C to calculate the total pressure in atmospheres is “
Want to see more full solutions like this?
Chapter 10 Solutions
Thinking Like an Engineer: An Active Learning Approach (3rd Edition)
Additional Engineering Textbook Solutions
BASIC BIOMECHANICS
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Thermodynamics: An Engineering Approach
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Fluid Mechanics: Fundamentals and Applications
- An unpressurized cylindrical tank with a 100-foot diameter holds a 40-foot column of water. What is total force acting against the bottom of the tank?arrow_forward7. In the following problems check to see if the set S is a vector subspace of the corresponding R. If it is not, explain why not. If it is, then find a basis and the dimension. (a) S = (b) S = {[],+,"} X1 x12x2 = x3 CR³ {[1], 4+4 = 1} CR³ X2arrow_forwardAAA Show laplace transform on 1; (+) to L (y(+)) : SY(s) = x (0) Y(s) = £ [lx (+)] = 5 x(+) · est de 2 -St L [ y (^) ] = So KG) et de D 2 D D AA Y(A) → Y(s) Ŷ (+) → s Y(s) -yarrow_forward
- 1) In each of the following scenarios, based on the plane of impact (shown with an (n, t)) and the motion of mass 1, draw the direction of motion of mass 2 after the impact. Note that in all scenarios, mass 2 is initially at rest. What can you say about the nature of the motion of mass 2 regardless of the scenario? m1 15 <+ m2 2) y "L χ m1 m2 m1 בז m2 Farrow_forward8. In the following check to see if the set S is a vector subspace of the corresponding Rn. If it is not, explain why not. If it is, then find a basis and the dimension. X1 (a) S = X2 {[2], n ≤ n } c X1 X2 CR² X1 (b) S X2 = X3 X4 x1 + x2 x3 = 0arrow_forward2) Suppose that two unequal masses m₁ and m₂ are moving with initial velocities V₁ and V₂, respectively. The masses hit each other and have a coefficient of restitution e. After the impact, mass 1 and 2 head to their respective gaps at angles a and ẞ, respectively. Derive expressions for each of the angles in terms of the initial velocities and the coefficient of restitution. m1 m2 8 m1 ↑ บา m2 ñ Вarrow_forward
- The fallowing question is from a reeds book on applied heat i am studying. Although the answer is provided, im struggling to understand the whole answer and the formulas and the steps theyre using. Also where some ov the values such as Hg and Hf come from in part i for example. Please explain step per step in detail thanks In an NH, refrigerator, the ammonia leaves the evaporatorand enters the cornpressor as dry saturated vapour at 2.68 bar,it leaves the compressor and enters the condenser at 8.57 bar with50" of superheat. it is condensed at constant pressure and leavesthe condenser as saturated liquid. If the rate of flow of the refrigerantthrough the circuit is 0.45 kglmin calculate (i) the compressorpower, (ii) the heat rejected to the condenser cooling water in kJ/s,an (iii) the refrigerating effect in kJ/s. From tables page 12, NH,:2.68 bar, hg= 1430.58.57 bar, hf = 275.1 h supht 50" = 1597.2Mass flow of refrigerant--- - - 0.0075 kgls 60Enthalpy gain per kg of refrigerant in…arrow_forwardstate the formulas for calculating work done by gasarrow_forwardExercises Find the solution of the following Differential Equations 1) y" + y = 3x² 3) "+2y+3y=27x 5) y"+y=6sin(x) 7) y"+4y+4y = 18 cosh(x) 9) (4)-5y"+4y = 10 cos(x) 11) y"+y=x²+x 13) y"-2y+y=e* 15) y+2y"-y'-2y=1-4x³ 2) y"+2y' + y = x² 4) "+y=-30 sin(4x) 6) y"+4y+3y=sin(x)+2 cos(x) 8) y"-2y+2y= 2e* cos(x) 10) y+y-2y=3e* 12) y"-y=e* 14) y"+y+y=x+4x³ +12x² 16) y"-2y+2y=2e* cos(x)arrow_forward
- The state of stress at a point is σ = -4.00 kpsi, σy = 16.00 kpsi, σ = -14.00 kpsi, Try = 11.00 kpsi, Tyz = 8.000 kpsi, and T = -14.00 kpsi. Determine the principal stresses. The principal normal stress σ₁ is determined to be [ The principal normal stress σ2 is determined to be [ The principal normal stress σ3 is determined to be kpsi. kpsi. The principal shear stress 71/2 is determined to be [ The principal shear stress 7½ is determined to be [ The principal shear stress T₁/, is determined to be [ kpsi. kpsi. kpsi. kpsi.arrow_forwardRepeat Problem 28, except using a shaft that is rotatingand transmitting a torque of 150 N * m from the left bearing to the middle of the shaft. Also, there is a profile keyseat at the middle under the load. (I want to understand this problem)arrow_forwardProb 2. The material distorts into the dashed position shown. Determine the average normal strains &x, Ey and the shear strain Yxy at A, and the average normal strain along line BE. 50 mm B 200 mm 15 mm 30 mm D ΕΙ 50 mm x A 150 mm Farrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





