
Concept explainers
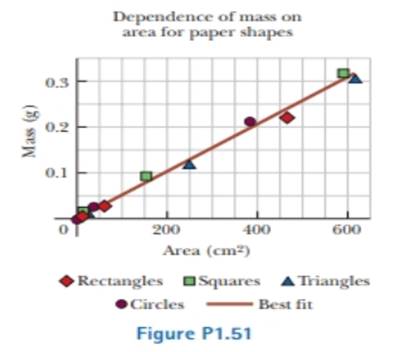
Review. A student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. He cuts out various shapes in various sizes, calculates their areas, measures their masses, and prepares the graph of Figure PI.51. (a) Consider the fourth experimental point from the top. How far is it from the best-lit straight line? Express your answer as a difference in vertical-axis coordinate, (b) Express your answer as a percentage, (c) Calculate the slope of the line, (d) State what the graph demonstrates, referring to the shape of the graph and the results of parts (b) and (c). (e) Describe whether this result should be expected theoretically, (f) Describe the physical meaning of the slope.
(a)
The distance of the fourth experimental point from the top from the best –fit straight line.
Answer to Problem 1.51P
The distance of the fourth experimental point from the top from the best fit straight line is
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
Consider the following figure.
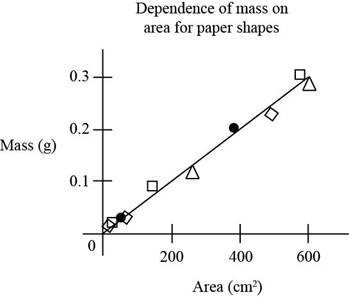
Figure (1)
Figure indicates the graph plotted area of pieces versus mass of the pieces of the paper.
The fourth experimental point from the top is a circle. It lies slightly above the best fit line.
From figure (1), the vertical coordinate for the forth experiment is
So the difference in the vertical axis coordinate is,
Here,
Substitute
Conclusion:
Therefore the distance of the fourth experimental point from the top from the best fit straight line is
(b)
The answer in the form of percentage.
Answer to Problem 1.51P
The answer in the form of percentage is
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
The expression for the percentage is,
Substitute
Conclusion:
Therefore the answer in the form of percentage is
(c)
The slope of the line.
Answer to Problem 1.51P
The slope of the line is
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
The expression for the slope is,
Here,
Substitute
Conclusion:
Therefore the slope of the line is
(d)
The demonstration from the graph referring to the shape of the graph and the results of part (b) and (c).
Answer to Problem 1.51P
The graph demonstrates that the mass of the cutout is proportional to its area for the shape cuts from this copy paper and the proportionality constant is
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
The graph given figure (1) demonstrates that the mass of the cutout in each shape is proportional to its area for the shape cuts from this copy paper and the proportionality constant is
The value of the slope from part (c) of the question and from the part (b) question the percentage uncertainty is
Conclusion:
Therefore the graph demonstrates that the mass of the cutout is proportional to its area for the shape cuts from this copy paper and the proportionality constant is
(e)
Whether this result should be expected theoretically or not.
Answer to Problem 1.51P
This result is to be expected theoretically if the paper has thickness and density that are uniform within the experimental uncertainty.
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
The graph given figure (1) demonstrates that the mass of the cutout in each shape is proportional to its area for the shape cuts from this copy paper and the proportionality constant is
The value of the slope from part (c) of the question is
Thus this result is expected theoretically when the object is having same aerial mass density and the paper has thickness and density that are uniform within the experimental uncertainty.
Conclusion:
Therefore this result is to be expected theoretically if the paper has thickness and density that are uniform within the experimental uncertainty.
(f)
The physical meaning of the slope.
Answer to Problem 1.51P
The physical meaning of the slope is the aerial density of the paper that represents the mass per unit area.
Explanation of Solution
Given data: The student is supplied with a stack of copy paper, ruler, compass, scissors, and a sensitive balance. A graph mass versus area is plotted for different sizes of the paper.
The graph given figure (1) demonstrates that the mass of the cutout in each shape is proportional to its area for the shape cuts from this copy paper and the proportionality constant is
The value of the slope from part (c) of the question is
The physical meaning of the slope is the aerial density of the paper that represent the mass per unit area.
Conclusion:
Therefore the physical meaning of the slope is the aerial density of the paper that represents the mass per unit area.
Want to see more full solutions like this?
Chapter 1 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
Additional Science Textbook Solutions
Biology: Concepts and Investigations
Applications and Investigations in Earth Science (9th Edition)
Biology: Life on Earth (11th Edition)
Organic Chemistry
Fundamentals Of Thermodynamics
Laboratory Manual For Human Anatomy & Physiology
- Below you will find 100 m split times for the American and France men’s 4x100 meter free style relay race during the 2008 Beijing Summer Olympics). Answer questions a-d. a) What was the total race time for each team, in seconds? b) Which team won the race? What was the difference in the teams’ times? c) What was the average speed for each team for the whole race? (provide answer to 3 decimal places). d) Calculate the average speed for each swimmer and report the results in a table like the one above. Remember to show the calculation steps. (provide answer to 3 decimal places). PLEASE SHOW ALL WORK AND STEPS.arrow_forwardNeed complete solution Pleasearrow_forwardBelow you will find 100 m split times for the American and France men’s 4x100 meter free style relay race during the 2008 Beijing Summer Olympics). Fill out the chart below. Calculate average speed per split (m/s). Show all work.arrow_forward
- No chatgpt pls will upvotearrow_forwardNo chatgpt plsarrow_forward4.4 A man is dragging a trunk up the loading ramp of a mover's truck. The ramp has a slope angle of 20.0°, and the man pulls upward with a force F whose direction makes an angle of 30.0° 75.0° with the ramp (Fig. E4.4). (a) How large a force F is necessary for the component Fx parallel to the ramp to be 90.0 N? (b) How large will the component Fy perpendicular to the ramp be then? Figure E4.4 30.0 20.0°arrow_forward
- 1. * A projectile is shot from a launcher at an angle e, with an initial velocity magnitude v., from a point even with a tabletop. The projectile lands on the tabletop a horizontal distance R (the "range") away from where it left the launcher. Set this up as a formal problem, and solve for vo (i.e., determine an expression for Vo in terms of only R, 0., and g). Your final equation will be called Equation 1.arrow_forward2. A projectile is shot from a launcher at an angle 0,, with an initial velocity magnitude vo, from a point even with a tabletop. The projectile hits an apple atop a child's noggin (see Figure 1). The apple is a height y above the tabletop, and a horizontal distance x from the launcher. Set this up as a formal problem, and solve for x. That is, determine an expression for x in terms of only v₁, o,y and g. Actually, this is quite a long expression. So, if you want, you can determine an expression for x in terms of v., 0., and time t, and determine another expression for timet (in terms of v., 0., y and g) that you will solve and then substitute the value of t into the expression for x. Your final equation(s) will be called Equation 3 (and Equation 4).arrow_forward4.56 ... CALC An object of mass m is at rest in equilibrium at the origin. At t = 0 a new force F(t) is applied that has components Fx(t) = k₁ + k₂y Fy(t) = k3t where k₁, k2, and k3 are constants. Calculate the position (1) and veloc- ity (t) vectors as functions of time.arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





