When a machine is functioning properly, only 3% of the items produced are defective. Assume that we will randomly select two parts produced on the machine and that we are interested in the number of defective parts found. Draw a tree diagram showing this problem as a two-trial experiment. How many experimental outcome results in exactly one defect being found. Compute the probability for i)No defects ii)Exactly one defect iii) Two defects
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
When a machine is
- Draw a tree diagram showing this problem as a two-trial experiment.
- How many experimental outcome results in exactly one defect being found.
- Compute the
probability for i)No defects ii)Exactly one defect iii) Two defects
1.)
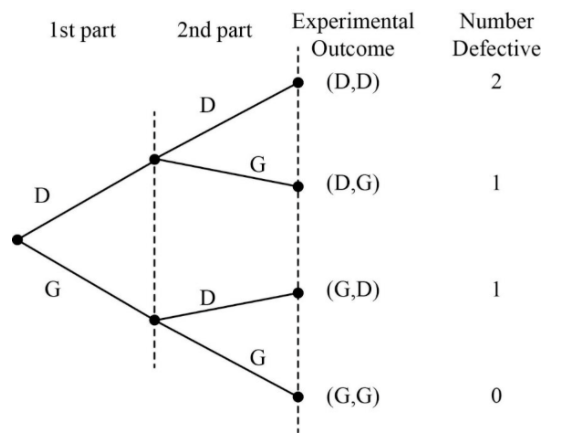
Tree diagram
A tree diagram can be used for organizing and summarizing the possible outcomes of an experiment and their probabilities.
Here, first branch of the tree denote the event that the produced part is defective (D) and the second branch of the tree denote the event that the produced part is not defective (G). There can be zero or one or two parts defective in the item produced by the machine.
The tree diagram representing the experiment is given below:
2)
The outcomes of the experiment are,
S= {(D, D),(D,G),(G,D),(G,G)}
The outcomes that resulted in exactly one defective is two.
3)
It was found that only 3% of the items produced are defective when the new machine is functioning properly. One is interested in the defective parts which are randomly selected from the two parts that are produced from the machine
Criteria for binomial distribution:
- Each experiment has fixed number of trials.
- Each trial is independent of the other.
- There are two possible outcomes. That are success and failure.
- Probability of success is same for all trials.
Define the random variable x as the number of defective parts found. Two parts produced on the machine are selected randomly. Therefore, number of samples (n) is 2. Each part is independent of the other. Also, there are two possible outcomes, the produced part is defective or the produced part is not defective (success or failure). It was found that 3% of the items produced is defective. Thus, the probability of success (p) is 0.03. Thus, x follows binomial distribution.
Thus, the conditions under which the given situation will be a binomial experiment are,
- The probability that a defective part is produced must be 0.3.
- The parts are selected independently.
The random variable X follows binomial n=2 and p=0.3
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 1 images









