Show that the following wave function is normalized. Remember to square it first. Limits of integration go from -infinity to infinity.
Q: for a particle inside a finite well its parity can either be even or odd. if the well is symmetric…
A: The parity is defined as
Q: Find the wave function and energy for the infinite-walled well problem Could you explain it to me…
A: The particle in a box (also known as the infinite potential well or the infinite square well) model…
Q: 5-6. The results found above apply also to the case of a pulse reflecting off a boundary. The type…
A: In this problem, we are dealing with the reflection and transmission of a pulse at a boundary…
Q: can you explain further, inside a finite well, the wave function is either cosine or sine, so…
A: For symmetric potential we can generalled the form of the wave function is either cosine or sine.…
Q: Design an FSM (Mealy machine) with one input, A, and one putout Q. Q should be 1 if the consecutive…
A: State Diagram-
Q: Consider a finite potential step as shown below, with V = V0 in the region x 0. Particles with…
A: The potential is given by,
Q: a zero-mean white Gaussian noise with power spectral pass filter with bandwidth B. . Find the…
A:
Q: (I) Simple quantum systems: potential barrier Consider a uniform potential barrier of height vo = 6…
A:
Q: Suppose there is a particle with mass m that is projected with energy E = V0 at the potential energy…
A: Step 1: We are given a 1-D potential barrier as shown in the figure whose potential function is…
Q: A particle of mass m is constrained to move between two concentric impermeable spheres of radii r =…
A:
Q: Use a trial function of the form e(-ax^2)/2 to calculate the ground state energy of a quartic…
A:
Q: Consider an Ising model of just two elementary dipoles, whose mutual interaction energy is ± E.…
A: Given, The two elementary dipoles, whose mutual interaction energy is ±E. The states of the system…
Q: For the potential well shown below, make a qualitative sketch of the two energy eigenstate wave…
A: Step 1: This problem can be solved by using the Schrodinger-Wave equation. If the particles…
Q: How can it be calculated if I only have probability flux and rate constant?
A: Entropy and heat dissipation in Markov processes are related to the thermodynamics of the system.…
Q: In atomic physics, the oscillator strength is defined as mho, Calculate the oscillator strength for…
A: Solution attached in the photo
Q: 7.25 With the previous problem in mind prove that dn (v) dv n₂ = n(v) + v i need clear ans
A: For the expression from problem 7.24 vg = cn+ ωdndω
Q: show that the following wave function is normalized.
A: The complex conjugate of above equation is
Q: The harmonic oscillator eigenfunction, n(x), is an odd function if n is even. True False
A:
Q: 2L Suppose a barrier qualifies as wide, and its height and width are such that ² √2mU₁ transmission…
A: The objective of this question is to calculate the transmission probabilities of a wide barrier when…
Q: 9x = exp(-/Bhv) 1- exp(-ßhv) Derive the partition function for a single harmonic oscillator in three…
A: Required derivation of partition function for simple harmonic oscillator.
Q: Consider a particle confined to an infinite square potential well with walls at x = 0 and x= L.…
A:
Q: in which ensembles ,open and closed assemblies are used?How can you connect lagrange undetermined…
A: Introduction: The statistical ensemble is a probability distribution for the system. Different…
Q: Find the corresponding Schrödinger equation and wave function, The energy for the infinite-walled…
A: Given: The infinitely walled well potential is given as V(x) = 0 ; 0 ≤ x ≤ a∞ ; 0 > x > a
Show that the following wave function is normalized. Remember to square it first. Limits of integration go from -infinity to infinity. DO NOT SKIP ANY STEPS IN THE PROCEDURE

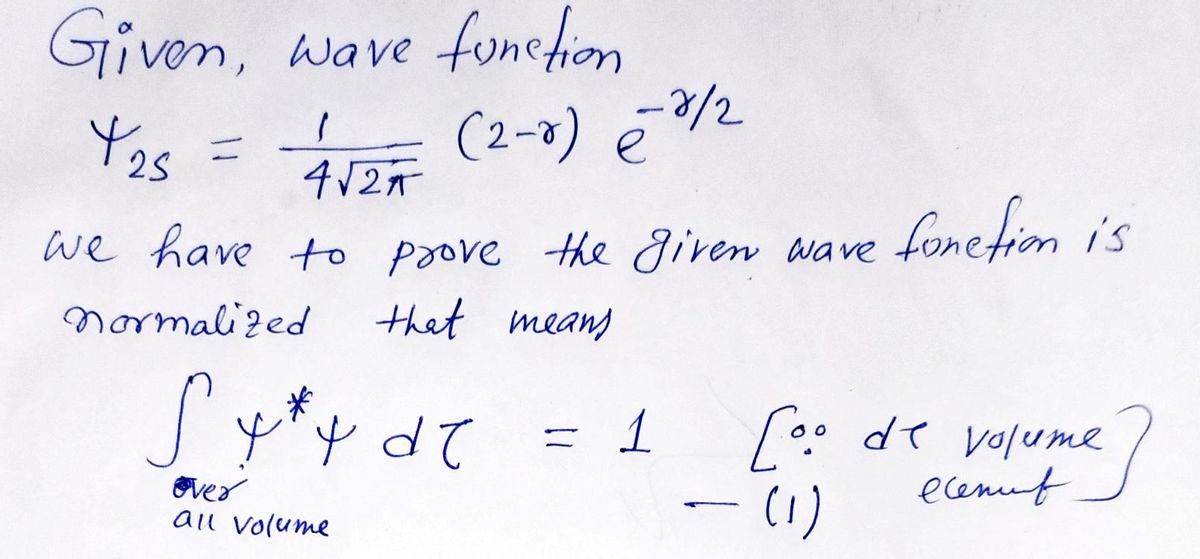
Step by step
Solved in 4 steps with 3 images

- Suppose that in a certain system a particle free to move along one dimension (with 0 ≤ x≤ ∞) is described by the unnormalized wavefunction ψ=e-ax with a=2m-1 What is the probability of finding the particle at a distance x≥1? (HINT: you will need to normalize the wavefunction first) show full and complete procedure. do not skip any stepsBy employing the prescribed definitions of the raising and lowering operators pertaining to the one-dimensional harmonic oscillator: x = ħ 2mω -(â+ + â_) hmw ê = i Compute the expectation values of the following quantities for the nth stationary staten. Keep in mind that the stationary states form an orthogonal set. 2 · (â+ − â_) [ pm 4ndx YmVndx = 8mn a. The position of particle (x) b. The momentum of the particle (p). c. (x²) d. (p²) e. Confirm that the uncertainty principle is satisfied for all values of nIn this question we will consider a finite potential well in which V = −V0 in the interval −L/2 ≤ x ≤ L/2, and V = 0 everywhere else (where V0 is a positive real number). For a particle with in the range −V0 < E < 0, write and solve the time-independent Schrodinger equation in the classically allowed and classically forbidden regions. Remember to keep the wavenumbers and exponential factors in your solutions real!
- The wavefunction for the motion of a particle on a ring is of the form ψ=NeimΦ . Evaluate the normalization constant, N. Show full and complete procedure in a clear way. DO NOT SKIP ANY STEPSolve the problem for a quantum mechanical particle trapped in a one dimensional box of length L. This means determining the complete, normalized wave functions and the possible energies. Please use the back of this sheet if you need more room.Needs Complete solution with 100 % accuracy.