samples exposed Dacter ghts bacteria, viruses, and tumors, was measured. Mean production went fr er tea drinking. The mean difference for the 5 subjects is 293 pg/mL with a s per implies that the use of the t-distribution is appropriate. ,et. al., "Antigens in tea-beverage prime human Vy2Vo2 T cells in vitro and kine responses," Proceedings of the National Academy of Sciences, May 13, 20

![### Confidence Interval Calculation
**Question:**
(b) Find a 90% confidence interval for the mean increase in the production of interferon gamma after drinking tea for one week.
**Instructions:**
- Round your answers to one decimal place.
**Answer Format:**
The 90% confidence interval is [ _______ ] to [ _______ ].
**Additional Information:**
- Your previous answer was marked as incorrect.
- This is your first attempt out of four allowed.
**Actions:**
- You can save your progress for later.
- Click "Submit Answer" to enter your solution.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F92bd98e7-680f-44cf-86fc-e198a10b6b67%2Fbf715838-c9e0-4d9a-bd79-57f28faf10b4%2F0lhqjm_processed.jpeg&w=3840&q=75)
In the given scenario, the blood samples of 5 participants are taken before and after one week of drinking about five cups of tea a day.
Here, the same participants are taken before and after one week of drinking about five cups of tea a day.
The most appropriate method used for the analysis is paired data in difference of means.
Let n denote the number of subjects.
Let denote the mean difference of the subjects and denote the standard deviation in the differences.
That is, n = 5
= 293 & = 242
The objective is to compute the 90% confidence interval for the mean .
The confidence level is,
C = 90%= 90/100= 0.90
The level of significance is,
The degrees of freedom is,
df = n-1= 5-1=4
from t table at 0.10 level of significance with 4 degrees of freedom the two- tailed critical value is,
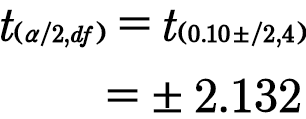
Step by step
Solved in 2 steps with 2 images









