Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
QUESTION 13 The only knowledge available about a given system S is that it is not causal. Let g [n] be its impulse response. What can be claimed exactly? For all n20, g[n] =0. For all n20, g[n] 0. There exists n2 0 such thatg [n] =0. There exists n 0 such that g [n]#0. For all n<0, g[n] =0. For all n<0, g[n] 0. There exists n <0 such that g [n]=0. There exists n <0 such that g [n] 0. O None of the above

QUESTION 13 The only knowledge available about a given system S is that it is not causal. Let g [n] be its impulse response. What can be claimed exactly? For all n20, g[n] =0. For all n20, g[n] 0. There exists n2 0 such thatg [n] =0. There exists n 0 such that g [n]#0. For all n<0, g[n] =0. For all n<0, g[n] 0. There exists n <0 such that g [n]=0. There exists n <0 such that g [n] 0. O None of the above

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question
100%
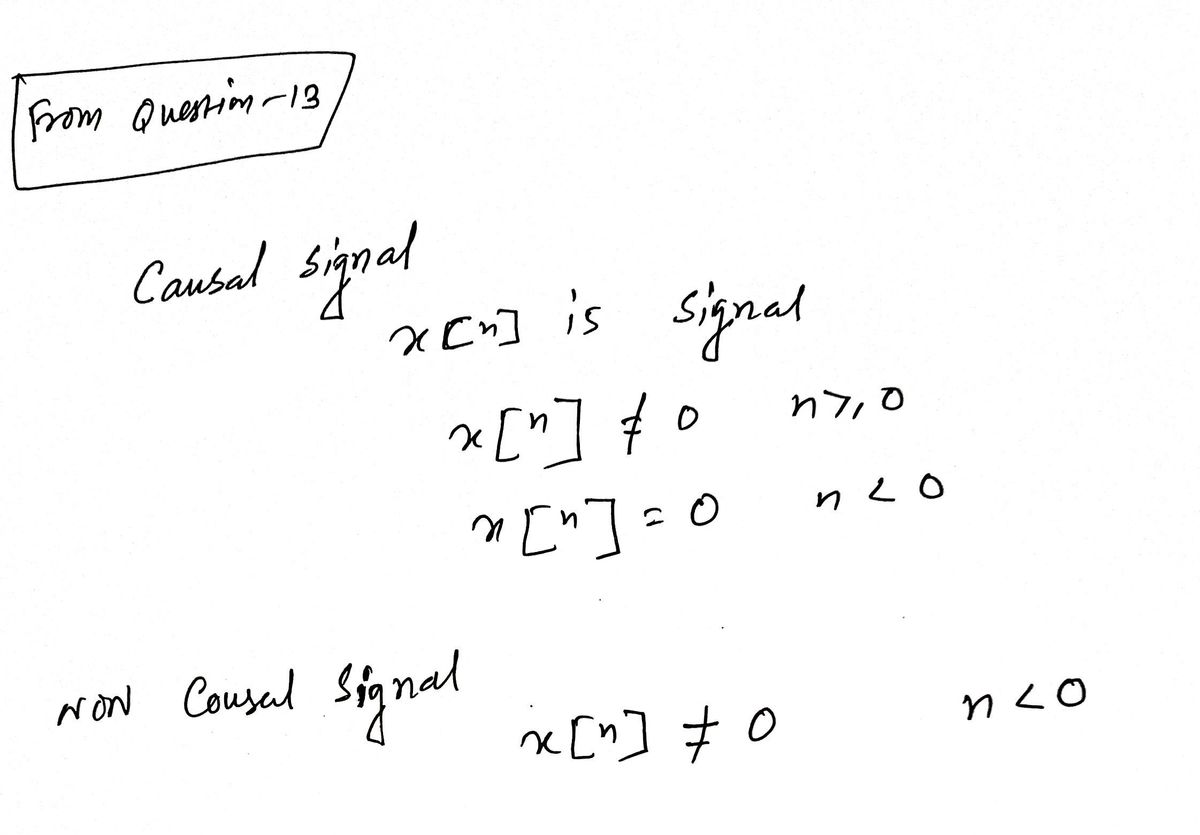
QUESTION 13 The only knowledge available about a given system S is that it is not causal. Let g [n] be its impulse response. What can be claimed exactly? For all n20, g [n] =0. For all n20, g[n] 0. There exists n2 0 such that g [n]=0. There exists n O such that g [n]#0. For all n<0, g[n] =0. For all n<0, g[n] 0. There exists n <0 such that g [n]=0. There exists n <0 such that g [n] 0. O None of the above QUESTION 14 Let S be the system such that {y[n]}= S({x [n]}) is defined by
Transcribed Image Text:QUESTION 13 The only knowledge available about a given system S is that it is not causal. Let g [n] be its impulse response. What can be claimed exactly? For all n20, g [n] =0. For all n20, g[n] 0. There exists n2 0 such that g [n]=0. There exists n O such that g [n]#0. For all n<0, g[n] =0. For all n<0, g[n] 0. There exists n <0 such that g [n]=0. There exists n <0 such that g [n] 0. O None of the above QUESTION 14 Let S be the system such that {y[n]}= S({x [n]}) is defined by
Expert Solution
Step 1

Electrical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS