Measurement of systolic blood pressure from nine patients with a certain condition and 11 healthy volunteers of similar age and gender were taken and recorded. Carryout hypothesis testing to determine if the mean pressures in the 2groups differ significantly. Data is in the table 1 below . Table 1: Systolic blood pressure from nine patients with a certain condition and 11 healthy volunteers of similar age and gender Patients X1 132 160 145 132 140 154 136 134 134 - - Controls X2 107 98 125 129 128 114 115 126 123 123 128 Df = (n1+n2-2) Calculated t= (Mean difference)/ [Standard Error Mean difference] Standard Error Mean difference = Sp {(1/n1+1/n2)}0.5 Sp2 = [(n1 -1) S12 + (n2-1) S22]/Df Critical value for the t-distribution = 2.010
Measurement of systolic blood pressure from nine patients with a certain condition and 11 healthy volunteers of similar age and gender were taken and recorded.
Carryout hypothesis testing to determine if the mean pressures in the 2groups differ significantly. Data is in the table 1 below .
Table 1: Systolic blood pressure from nine patients with a certain condition and 11 healthy volunteers of similar age and gender
|
Patients |
X1 |
132 |
160 |
145 |
132 |
140 |
154 |
136 |
134 |
134 |
- |
- |
|
Controls |
X2 |
107 |
98 |
125 |
129 |
128 |
114 |
115 |
126 |
123 |
123 |
128 |
Df = (n1+n2-2)
Calculated t= (Mean difference)/ [Standard Error Mean difference]
Standard Error Mean difference = Sp {(1/n1+1/n2)}0.5
Sp2 = [(n1 -1) S12 + (n2-1) S22]/Df
Critical value for the t-distribution = 2.010
Hypotheses for the test are given below:
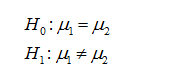
Enter the values in columns A and B of excel.
The sample mean for the first sample is 140.778 (using the Excel function, =AVERAGE(A1:A9).
The sample standard deviation is 10.195 (using the Excel function, =STDEV(A1:A9).
The sample mean for the second sample is 119.636 (using the Excel function, =AVERAGE(B1:B11).
The sample standard deviation is 10.003 (using the Excel function, =STDEV(B1:B11).
Step by step
Solved in 5 steps with 4 images









