Let x represent the number of mountain climbers killed each year. The long-term variance of x is approximately σ2 = 136.2. Suppose that for the past 8 years, the variance has been s2 = 119.0. Use a 1% level of significance to test the claim that the recent variance for number of mountain-climber deaths is less than 136.2. Find a 90% confidence interval for the population variance. 1. Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.) 2. What are the degrees of freedom? 3. Find the requested confidence interval for the population variance. (Round your answers to two decimal places.) lower limit upper limit
Let x represent the number of mountain climbers killed each year. The long-term variance of x is approximately σ2 = 136.2. Suppose that for the past 8 years, the variance has been s2 = 119.0. Use a 1% level of significance to test the claim that the recent variance for number of mountain-climber deaths is less than 136.2. Find a 90% confidence interval for the population variance.
1. Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.)
2. What are the degrees of freedom?
3. Find the requested confidence interval for the population variance. (Round your answers to two decimal places.)
lower limit
upper limit
1.
Test statistic:
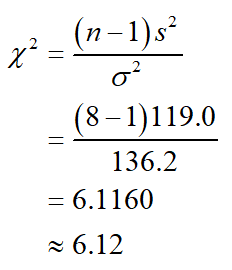
Thus, the test statistic is 6.12.
2.
The degrees of freedom is, that the test statistic follows chi-square distribution with n-1 degrees. That is, with 7(=8-1) degrees of freedom.
Step by step
Solved in 3 steps with 2 images









