Answered: For motion in a plane with the… | bartleby

Related questions

Question

For motion in a plane with the Hamiltonian
H = |p|ⁿ − a r⁻ⁿ,
where p is the vector of the momenta conjugate to the Cartesian coordinates,
show that there is a constant of the motion
D = (p . r) / n − H t.

Expert Solution

Step 1

Given:

The Hamiltonian of the motion in a plane is

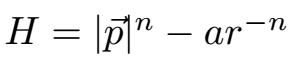
The operator

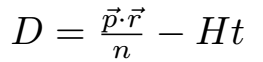
Step by step

Solved in 4 steps with 7 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

(a) For one-dimensional motion of a particle of mass m acted upon by a force F(x), obtain the formal solution to the trajectory x(t) in the inverse form: m = ₂√ 2 {E – V(x)} where V (x) is the potential energy and x0 is the position at t = 0. (b) If the force, F(x) is a constant then what is the equation of the particles trajectory (x vs t). t(x): = dx
Express the Lagrangian for a free particle moving in a plane in a plane polar coordinates. From this proves that, in terms of radial and tangential components, the acceleration inpolar coordinates isa = (¨r − rθ˙2) er + (rθ¨ + 2 r˙ θ˙) eθ(where er and eθ are unit vectors in the positive radial and tangential directions).
A particle of mass m described by one generalized coordinate q movesunder the influence of a potential V(q) and a damping force −2mγq˙ proportional to its velocity with the Lagrangian L = e2γt(1/2 * mq˙2 − V (q)) which gives the desired equation of motion. (a) Consider the following generating function: F = eγtqP - QP.Obtain the canonical transformation from (q,p) to (Q,P) and the transformed Hamiltonian K(Q,P,t). (b) Let V (q) = (1/2)mω2q2 be a harmonic potential with a natural frequency ω and note that the transformed Hamiltonian yields a constant of motion. Obtain the solution Q(t) for the damped oscillator in the under damped case γ < ω by solving Hamilton's equations in the transformed coordinates. Then, write down the solution q(t) using the canonical coordinates obtained in part (a).
In a Hamiltonian system, what are the conditions for fixed points?
Consider a particle of mass m undergoing simple harmonic motion. The force on the particle is given by Hooke's law F(x)=-kx. Determine the equation of motion by using the Euler-Lagrange equation.
Let G(u, v) = (3u + v, u - 2v). Use the Jacobian to determine the area of G(R) for: (a) R = [0, 3] x [0, 5] (b) R = [2, 5] x [1, 7]
A block of mass m = 240 kg rests against a spring with a spring constant of k = 550 N/m on an inclined plane which makes an angle of θ degrees with the horizontal. Assume the spring has been compressed a distance d from its neutral position. Refer to the figure. (a) Set your coordinates to have the x-axis along the surface of the plane, with up the plane as positive, and the y-axis normal to the plane, with out of the plane as positive. Enter an expression for the normal force, FN, that the plane exerts on the block (in the y-direction) in terms of defined quantities and g. (b) Denoting the coefficient of static friction by μs, write an expression for the sum of the forces in the x-direction just before the block begins to slide up the inclined plane. Use defined quantities and g in your expression. (c) Assuming the plane is frictionless, what will the angle of the plane be, in degrees, if the spring is compressed by gravity a distance 0.1 m? (d) Assuming θ = 45 degrees and the…
(a) What does the quadrupole formula (P) = = = (Qij Q³ ³) compute? Reason the answer. (b) A point mass m undergoes a harmonic motion along the z-axis with frequency w and amplitude L, x(t) = y(t) = 0, z(t) = L cos(wt). Show that the only non-vanishing component of the quadrupole moment tensor is = Im L² cos² (wt). (c) Use the quadrupole formula to compute the power radiated by the emission of gravitational waves. (Hint: recall that (cos(t)) = (sin(t)) = 0 and (cos² (t)) = (sin² (t)) = ½½ for a given frequency 2.)