(c) The motion of a particle in a plane is governed by the Lagrangian (a² + ÿ²) + ¿(y& – xỷ). L = (i) Obtain the equations of motion (simplify if possible). Is the force acting on the particle conservative? (ii) Verify that x = Rcost, y = Rsin t, is a solution of the equations of motion (here R is a constant).
(c) The motion of a particle in a plane is governed by the Lagrangian (a² + ÿ²) + ¿(y& – xỷ). L = (i) Obtain the equations of motion (simplify if possible). Is the force acting on the particle conservative? (ii) Verify that x = Rcost, y = Rsin t, is a solution of the equations of motion (here R is a constant).
Related questions
Question

Transcribed Image Text:(c) The motion of a particle in a plane is governed by the Lagrangian
1
L =
2
} (4² + s®) + ¿vż – zý).
1
+ j) + (yi – xỷ).
(i) Obtain the equations of motion (simplify if possible). Is the force acting on the
particle conservative?
(ii) Verify that
x = Rcost,
y = Rsin t,
is a solution of the equations of motion (here R is a constant).
Expert Solution
Step 1
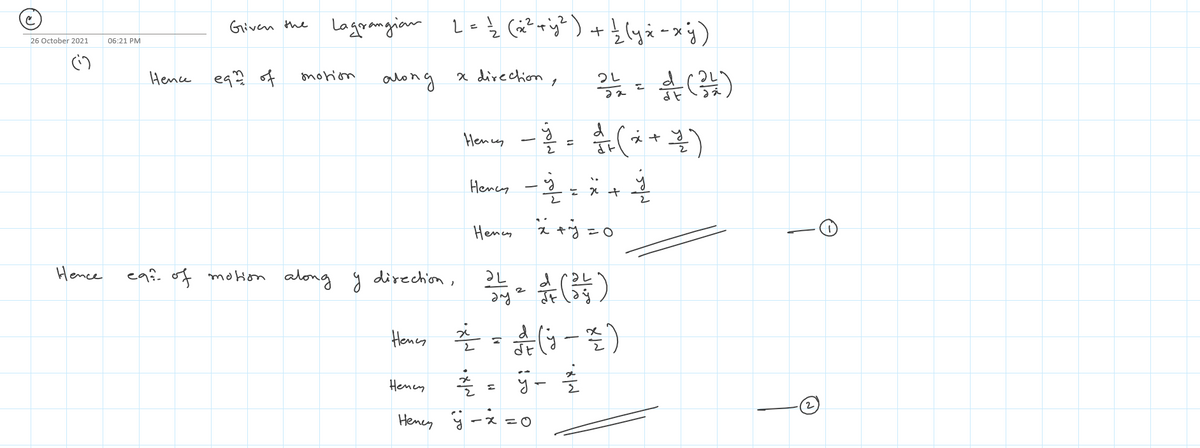
Step by step
Solved in 2 steps with 2 images
