Exercise 0.8. Write out the full details of the previous proof, and also show the converse of Proposition 1 holds. That is, if (11) holds for all o, 1 € dom(f) and 0 ≤ x ≤ 1, then f(.) is convex. Dug of in
Exercise 0.8. Write out the full details of the previous proof, and also show the converse of Proposition 1 holds. That is, if (11) holds for all o, 1 € dom(f) and 0 ≤ x ≤ 1, then f(.) is convex. Dug of in
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%

Transcribed Image Text:Exercise 0.8. Write out the full details of the previous proof, and also show the converse of
Proposition 1 holds. That is, if (11) holds for all o, ₁ € dom(f) and 0 ≤ x ≤ 1, then f(.)
is convex.
Proof is at the bottom
Proposition 1. Suppose f(): R → R is convex. Then for every To, 1 € dom(f), To ‡ ₁
and 0<x< 1, we have
See Figure 5:
f(xx)-f(xo)
X(x₁ - x0)
f(x1)
f(xo)
f(xx)
m1
epi(f)
To
f(x₁) = f(x)
(x1 - x0)
slope=m₁
Į
XX
m2
f(x₁)-f(xx)
(1-X)(x₁ - xo),
slope= m₂
21
m3
slope=m3
Figure 5: The 3-point property
(11)
Proof. Assume f() is convex with xo x₁ € R" belonging to dom(f) and 0 < X < 1. Then
f(xx) = f((1-X)x₁ + Xx₁) ≤ (1 − A)f(x) + f(x₁).
(12)
The right-hand side of (12) equals f(zo) + X(ƒ (x₁) − ƒ (x₁)), and then rearranging terms
in (12) and dividing by A gives the first inequality in (11). The right-hand side of (12) also
equals f(x₁) + (1-x)(ƒ(xo) – ƒ (x₁)), and again rearranging terms in (12) and dividing by
(1 - A) gives the second inequality in (11).
Expert Solution
Step 1
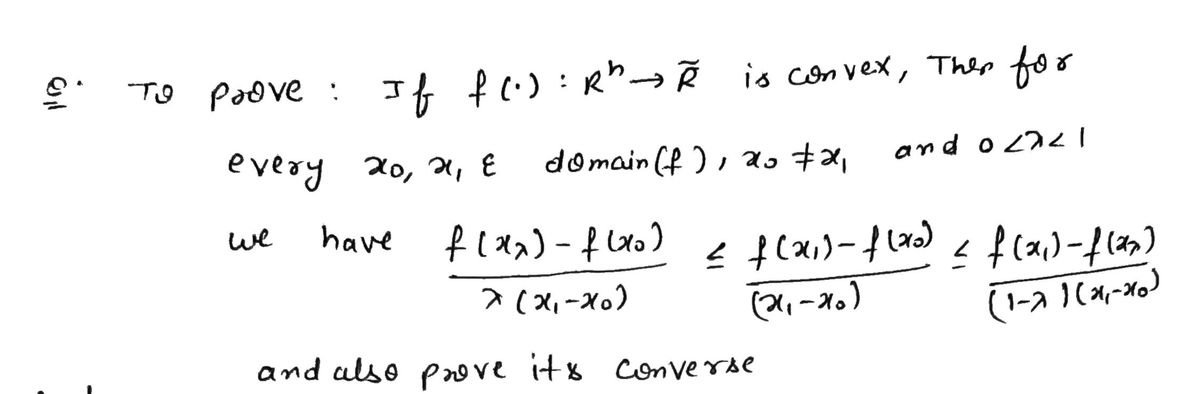
Step by step
Solved in 3 steps with 3 images

Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

