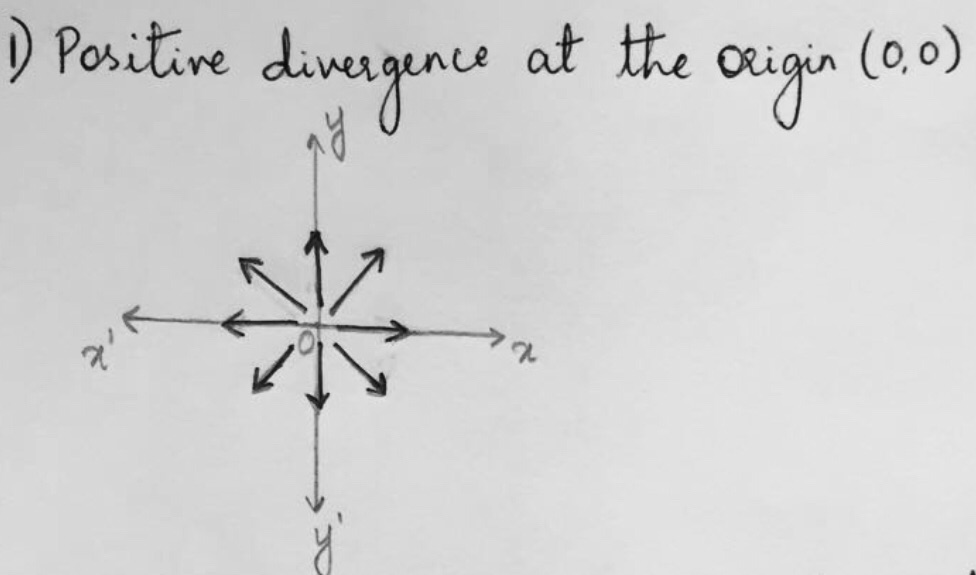
Draw a vector field with... 1. Positive divergence at the origin. 2. Positive divergence at (1,0) and positive divergence at (-1,0). 3. Positive divergence at (1,0) and negative divergence at (-1,0).
Calculus III problem: Vector field
Draw a vector field with...
1. Positive divergence at the origin.
2. Positive divergence at (1,0) and positive divergence at (-1,0).
3. Positive divergence at (1,0) and negative divergence at (-1,0).
4. Curl at the origin that is in the positive z-direction.
5. Curl at (1,0) in the positive z-direction, and curl at (-1,0) in the positive z-direction.
6. Curl at (1,0) in the positive z-direction, and curl at (-1,0) in the negative z-direction.
7. Zero divergence and zero curl everywhere.
8. Both nonzero divergence and nonzero curl at the origin.
Hey there, since your question has multiple sub-parts. We have solved the first three parts for you. Please re-post the question and highlight the unresolved ones.
Divergence can be defined as a measure of change in density of a fluid flowing in a given vector field.
Positive divergence, is also called as source it is the field in which the field is moving outwards.
Negative divergence, is also called as sink it is the field in which the field is moving inwards.
Step by step
Solved in 4 steps with 3 images
