According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance? Because npo (1-Po) =10, the sample size is (Round to one decimal place as needed.) 5% of the population size, and the sample the requirements for testing the hypothesis ▼satisfied.
According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance? Because npo (1-Po) =10, the sample size is (Round to one decimal place as needed.) 5% of the population size, and the sample the requirements for testing the hypothesis ▼satisfied.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
![**Text:**
According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance?
---
Because np₀(1 - p₀) = [ ] [Dropdown Menu] 10, the sample size is [Dropdown Menu] 5% of the population size, and the sample [Dropdown Menu] the requirements for testing the hypothesis [Dropdown Menu] satisfied.
(Round to one decimal place as needed.)
**Instructions for Completing Dropdowns:**
1. Fill in the calculations to determine if np₀(1 - p₀) is greater than or equal to 10.
2. Determine if the sample size is less than 5% of the population size.
3. Conclude if the sample meets the requirements for hypothesis testing.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fac3be618-b645-4bd8-855b-808ff3fc18d4%2F4962dd5b-4766-4140-bf30-ee41c8c9910e%2Ftjoypu_processed.png&w=3840&q=75)
Transcribed Image Text:**Text:**
According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance?
---
Because np₀(1 - p₀) = [ ] [Dropdown Menu] 10, the sample size is [Dropdown Menu] 5% of the population size, and the sample [Dropdown Menu] the requirements for testing the hypothesis [Dropdown Menu] satisfied.
(Round to one decimal place as needed.)
**Instructions for Completing Dropdowns:**
1. Fill in the calculations to determine if np₀(1 - p₀) is greater than or equal to 10.
2. Determine if the sample size is less than 5% of the population size.
3. Conclude if the sample meets the requirements for hypothesis testing.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 10 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
![According to a government agency for a large country, the proportion of fatal traffic accidents involving drivers with a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance?
**Sample Size Check:**
Because \( n p_0 (1 - p_0) = 24.5 > 10 \), the sample size is less than 5% of the population size, and the sample is given to be random, the requirements for testing the hypothesis are satisfied.
**Hypotheses:**
- Null Hypothesis (\( H_0 \)): \( p = 0.34 \)
- Alternative Hypothesis (\( H_1 \)): \( p > 0.34 \)
*Type integers or decimals. Do not round.*
**Test Statistic Calculation:**
\( z_0 = 2.62 \)
*(Round to two decimal places as needed.)*
**P-Value:**
P-value = \[ \ \]
*(Round to three decimal places as needed.)*](https://content.bartleby.com/qna-images/question/ac3be618-b645-4bd8-855b-808ff3fc18d4/e662c284-40f5-4e66-aa9a-d3f5cebf88ad/p5w8id_thumbnail.png)
Transcribed Image Text:According to a government agency for a large country, the proportion of fatal traffic accidents involving drivers with a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance?
**Sample Size Check:**
Because \( n p_0 (1 - p_0) = 24.5 > 10 \), the sample size is less than 5% of the population size, and the sample is given to be random, the requirements for testing the hypothesis are satisfied.
**Hypotheses:**
- Null Hypothesis (\( H_0 \)): \( p = 0.34 \)
- Alternative Hypothesis (\( H_1 \)): \( p > 0.34 \)
*Type integers or decimals. Do not round.*
**Test Statistic Calculation:**
\( z_0 = 2.62 \)
*(Round to two decimal places as needed.)*
**P-Value:**
P-value = \[ \ \]
*(Round to three decimal places as needed.)*
Solution
Follow-up Question
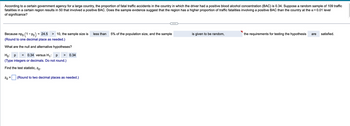
Transcribed Image Text:According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.34. Suppose a random sample of 109 traffic fatalities in a certain region results in 50 that involved a positive BAC. Does the sample evidence suggest that the region has a higher proportion of traffic fatalities involving a positive BAC than the country at the α = 0.01 level of significance?
---
Because \( np_0 (1 - p_0) = 24.5 > 10 \), the sample size is less than 5% of the population size, and the sample is given to be random, the requirements for testing the hypothesis are satisfied.
What are the null and alternative hypotheses?
\( H_0: \, p = 0.34 \) versus \( H_1: \, p > 0.34 \)
(Type integers or decimals. Do not round.)
Find the test statistic, \( z_0 \).
\( z_0 = \) _____ (Round to two decimal places as needed.)
Solution
Follow-up Question

Transcribed Image Text:**Hypothesis Testing for Proportion Problems in Traffic Fatalities**
In this example, a government agency reports that for a large country, the proportion of fatal traffic accidents involving drivers with a positive blood alcohol concentration (BAC) is 0.34. We have a random sample of 109 traffic fatalities from a specific region, in which 50 cases involved a positive BAC. The question is whether this region has a higher proportion of such traffic fatalities compared to the entire country, using a significance level of α = 0.01.
### Conditions Verification
- **Sample Size Condition**:
Calculate \( np_0 (1 - p_0) = 24.5 \). Since this value is greater than 10, the sample size condition is met.
- **Population Size Condition**:
The sample size is less than 5% of the entire population.
- **Random Sampling Condition**:
The sample is stated to be random.
Since all conditions are satisfied, the hypothesis test requirements are met.
### Hypotheses Formulation
- **Null Hypothesis (H₀)**:
\( p = 0.34 \) (The proportion of traffic fatalities involving a positive BAC in the region is equal to the national proportion.)
- **Alternative Hypothesis (H₁)**:
\( p > 0.34 \) (The proportion of traffic fatalities involving a positive BAC in the region is greater than the national proportion.)
By conducting this hypothesis test, we aim to determine if the region indeed has a higher incidence of BAC-related traffic fatalities compared to the national average, at a 1% level of significance.
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman