A pendulum is a harmonic oscillator and suppose that once it is set into motion, it follows simple harmonic motion. We will assume that its equilibrium position is when it is hanging exactly vertically at rest. When it is to the right of the equilibrium position it has positive displacement; to the left of equilibrium position is negative displacement. For a particular pendulum, the following observations are made: • It is initially at its equilibrium position. • It is pushed to the right by a force to set it into motion at t = 0. • At its maximum displacement, it is 5 inches away from the equilibrium position. • It completes one cycle of motion in 0.5 seconds. a.) Determine a model for the displacement of the end of the pendulum d (in inches) as a function of time t (in seconds). b.) At what times is the end of the pendulum furthest from the equilibrium position? There are many times when this occurs due to the oscillation it experiences. List a few times and describe the pattern
A pendulum is a harmonic oscillator and suppose that once it is set into motion, it follows
simple harmonic motion. We will assume that its equilibrium position is when it is hanging exactly
vertically at rest. When it is to the right of the equilibrium position it has positive displacement; to the
left of equilibrium position is negative displacement.
For a particular pendulum, the following observations are made:
• It is initially at its equilibrium position.
• It is pushed to the right by a force to set it into motion at t = 0.
• At its maximum displacement, it is 5 inches away from the equilibrium position.
• It completes one cycle of motion in 0.5 seconds.
a.) Determine a model for the displacement of the end of the pendulum d (in inches) as a function
of time t (in seconds).
b.) At what times is the end of the pendulum furthest from the equilibrium position? There are
many times when this occurs due to the oscillation it experiences. List a few times and describe the pattern
(a)
The general displacement equation of a SHM is:
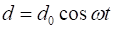
The formula for the angular frequency is:
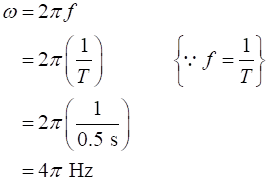
Substitute the known values in the general equation of SHM and solve.
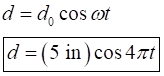
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 5 images









