A matrix A and an echelon form of A are shown below. Find a basis for Col A and a basis for Nul A. A = 57 3 - 26 4 64-14 23 2-12 Find a basis for Col A. 1 2 3 - 10 014 -8 000 0
A matrix A and an echelon form of A are shown below. Find a basis for Col A and a basis for Nul A. A = 57 3 - 26 4 64-14 23 2-12 Find a basis for Col A. 1 2 3 - 10 014 -8 000 0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Matrix and Echelon Form
A matrix \( A \) and an echelon form of \( A \) are shown below. Find a basis for \( \text{Col } A \) and a basis for \( \text{Nul } A \).
\[
A = \begin{bmatrix}
5 & 7 & 3 & -26 \\
6 & 4 & -14 & 4 \\
2 & 3 & 2 & -12
\end{bmatrix}
\sim
\begin{bmatrix}
1 & 2 & 3 & -10 \\
0 & 1 & 4 & -8 \\
0 & 0 & 0 & 0
\end{bmatrix}
\]
---
### Instructions
**Find a basis for \( \text{Col } A \).**
- Identify the pivot columns in the echelon form of the matrix.
- Use the corresponding columns from the original matrix \( A \) to form a basis for \( \text{Col } A \).
**Identifying Pivot Columns:**
1. The first column [1, 0, 0] corresponds to a pivot column.
2. The second column [2, 1, 0] corresponds to a pivot column.
Use the columns from the original matrix \( A \) that correspond to the pivot columns:
- Column 1 from matrix \( A \): \([5, 6, 2]\)
- Column 2 from matrix \( A \): \([7, 4, 3]\)
Thus, the basis for \( \text{Col } A \) is \(\{ [5, 6, 2], [7, 4, 3] \}\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2432691a-c29a-4a02-b85a-93b716867369%2Fcf810422-5d55-4864-a200-7d3046f3eba4%2F78wvm3b_processed.png&w=3840&q=75)
Transcribed Image Text:### Matrix and Echelon Form
A matrix \( A \) and an echelon form of \( A \) are shown below. Find a basis for \( \text{Col } A \) and a basis for \( \text{Nul } A \).
\[
A = \begin{bmatrix}
5 & 7 & 3 & -26 \\
6 & 4 & -14 & 4 \\
2 & 3 & 2 & -12
\end{bmatrix}
\sim
\begin{bmatrix}
1 & 2 & 3 & -10 \\
0 & 1 & 4 & -8 \\
0 & 0 & 0 & 0
\end{bmatrix}
\]
---
### Instructions
**Find a basis for \( \text{Col } A \).**
- Identify the pivot columns in the echelon form of the matrix.
- Use the corresponding columns from the original matrix \( A \) to form a basis for \( \text{Col } A \).
**Identifying Pivot Columns:**
1. The first column [1, 0, 0] corresponds to a pivot column.
2. The second column [2, 1, 0] corresponds to a pivot column.
Use the columns from the original matrix \( A \) that correspond to the pivot columns:
- Column 1 from matrix \( A \): \([5, 6, 2]\)
- Column 2 from matrix \( A \): \([7, 4, 3]\)
Thus, the basis for \( \text{Col } A \) is \(\{ [5, 6, 2], [7, 4, 3] \}\).
Expert Solution
Step 1: Introduction to given details
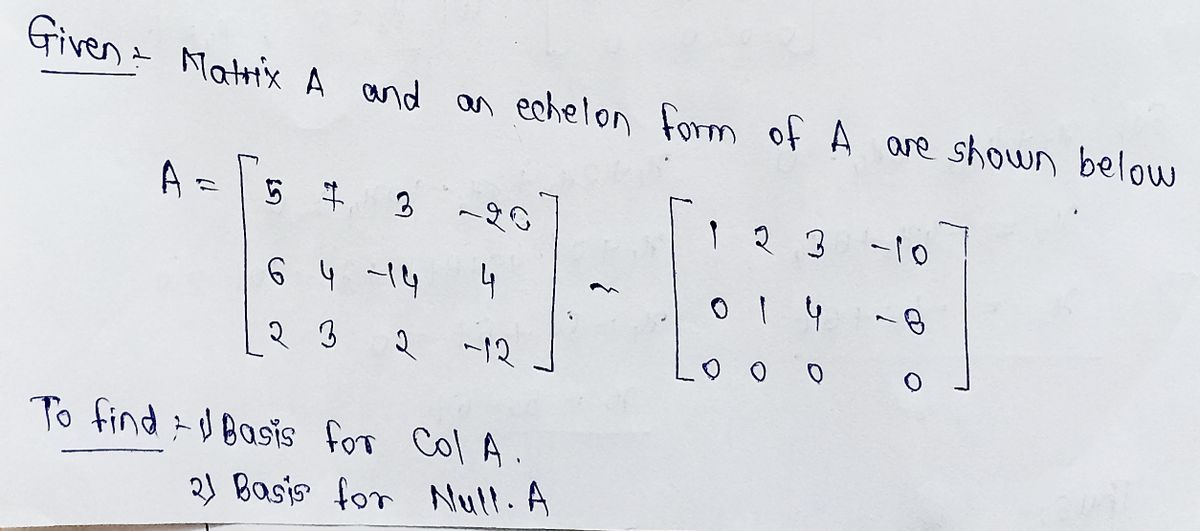
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

