A matrix A and an echelon form of A are shown below. Find a basis for Col A and a basis for Nul A. A = 1 2 - 1 -4 - 10 - 2 0 3 10 3 - 3 - 15 2 9 8 4 14 23 -7 - 33 Find a basis for Col A. w 16 17 0 4 02 70-1 00 01 7 00 00 0
A matrix A and an echelon form of A are shown below. Find a basis for Col A and a basis for Nul A. A = 1 2 - 1 -4 - 10 - 2 0 3 10 3 - 3 - 15 2 9 8 4 14 23 -7 - 33 Find a basis for Col A. w 16 17 0 4 02 70-1 00 01 7 00 00 0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Matrix Analysis: Basis for Column Space and Null Space
A matrix \( A \) and its echelon form are shown below. Follow the process to find a basis for the column space (\(\text{Col } A\)) and null space (\(\text{Nul } A\)) of matrix \( A \).
#### Matrix \( A \):
\[
A = \begin{bmatrix}
1 & 2 & 3 & -3 & -15 \\
-1 & -4 & -10 & 2 & 9 \\
-2 & 0 & 8 & 4 & 14 \\
3 & 10 & 23 & -7 & -33
\end{bmatrix}
\]
#### Echelon Form of \( A \):
\[
\sim \begin{bmatrix}
1 & 6 & 17 & 0 & 4 \\
0 & 2 & 7 & 0 & -1 \\
0 & 0 & 1 & 1 & 7 \\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
\]
The echelon form provides insight into linearly independent columns, helping identify pivot columns. These columns in the original matrix \( A \) represent the basis for the column space.
#### Finding a Basis for \(\text{Col } A\):
Consider the pivot positions in the echelon form of \( A \):
- Pivot columns are the first, second, and third columns.
Extract corresponding columns from the original matrix \( A \):
\[
\begin{bmatrix}
1 & 2 & 3 \\
-1 & -4 & -10 \\
-2 & 0 & 8 \\
3 & 10 & 23
\end{bmatrix}
\]
These form the basis for \(\text{Col } A\).
In addition to \(\text{Col } A\), we would proceed to find \(\text{Nul } A\) by solving \( A\mathbf{x} = \mathbf{0} \) through back substitution on the echelon form, focusing on free variables (non-pivot columns).
This content layout clearly demonstrates the step-by-step method and underlying principles for identifying bases in linear algebra, supporting both understanding and application.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2432691a-c29a-4a02-b85a-93b716867369%2F60a59f84-a1ab-4830-baed-d1491214e9eb%2Fkz42yxe_processed.png&w=3840&q=75)
Transcribed Image Text:### Matrix Analysis: Basis for Column Space and Null Space
A matrix \( A \) and its echelon form are shown below. Follow the process to find a basis for the column space (\(\text{Col } A\)) and null space (\(\text{Nul } A\)) of matrix \( A \).
#### Matrix \( A \):
\[
A = \begin{bmatrix}
1 & 2 & 3 & -3 & -15 \\
-1 & -4 & -10 & 2 & 9 \\
-2 & 0 & 8 & 4 & 14 \\
3 & 10 & 23 & -7 & -33
\end{bmatrix}
\]
#### Echelon Form of \( A \):
\[
\sim \begin{bmatrix}
1 & 6 & 17 & 0 & 4 \\
0 & 2 & 7 & 0 & -1 \\
0 & 0 & 1 & 1 & 7 \\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
\]
The echelon form provides insight into linearly independent columns, helping identify pivot columns. These columns in the original matrix \( A \) represent the basis for the column space.
#### Finding a Basis for \(\text{Col } A\):
Consider the pivot positions in the echelon form of \( A \):
- Pivot columns are the first, second, and third columns.
Extract corresponding columns from the original matrix \( A \):
\[
\begin{bmatrix}
1 & 2 & 3 \\
-1 & -4 & -10 \\
-2 & 0 & 8 \\
3 & 10 & 23
\end{bmatrix}
\]
These form the basis for \(\text{Col } A\).
In addition to \(\text{Col } A\), we would proceed to find \(\text{Nul } A\) by solving \( A\mathbf{x} = \mathbf{0} \) through back substitution on the echelon form, focusing on free variables (non-pivot columns).
This content layout clearly demonstrates the step-by-step method and underlying principles for identifying bases in linear algebra, supporting both understanding and application.
Expert Solution
Step 1: Description
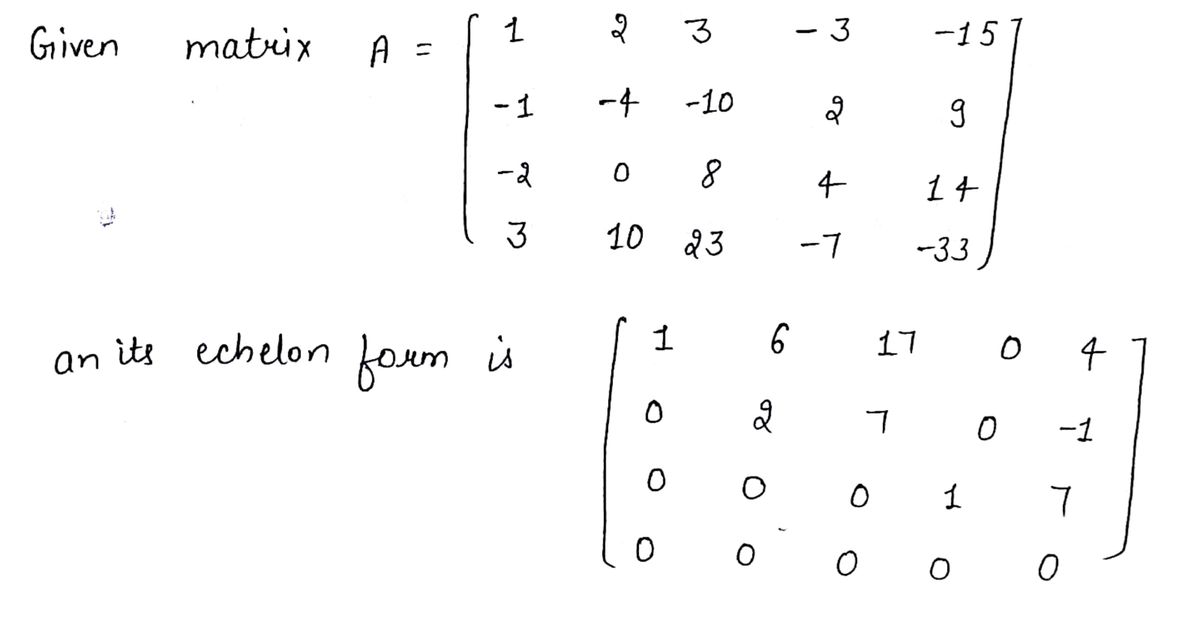
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

