Answered: A hospital claims that the proportion,…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

A hospital claims that the proportion,

, of full-term babies born in their hospital that weigh more than

pounds is

48%

. In a random sample of

155

babies born in this hospital,

weighed over

pounds. Is there enough evidence to reject the hospital's claim at the

0.1

level of significance?

Perform a two-tailed test. Then fill in the table below.

Carry your intermediate computations to at least three decimal places and round your answers as specified in the table.

The null hypothesis:	H0:
The alternative hypothesis:	H1:
The type of test statistic:	(Choose one)ZtChi squareF

The value of the test statistic: (Round to at least three decimal places.)
The two critical values at the 0.1 level of significance: (Round to at least three decimal places.)	and
Can we reject the claim that the proportion of full-term babies born in their hospital that weigh more than 7 pounds is 48% ?	Yes	No

Expert Solution

Step 1

Given:

Claimed proportion of babies weighing more than 7 pounds (p) = 0.48

Sample size of babies born in the hospital (n) = 155

Number of babies in the sample weighing above 7 pounds (x) = 87

Significance level = 0.1

Step 2

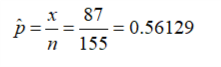
Testing whether the proportion of babies born weighing more than 7 pounds is different from 0.48 or not.

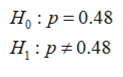
Test statistic

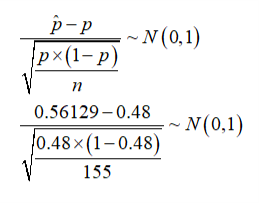
The test value is 2.0257.

Critical value

From z tables

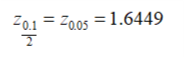
Conclusion:

As the test value does not lies within (-1.6449, 1.6449) , so there is sufficient evidence to reject null hypothesis at 0.1 level of significance and thus conclude that the hospital’s claim regarding the proportion of babies weighing above 7 pounds is 0.48 is incorrect.

Step by step

Solved in 3 steps with 6 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Proportions$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions