A factor in determining the usefulness of an examination as a measure of demonstrated ability is the amount of spread that occurs in the grades. If the spread or variation of examination scores is very small, it usually means that the examination was either too hard or too easy. However, if the variance of scores is moderately large, then there is a definite difference in scores between "better," "average," and "poorer" students. A group of attorneys in a midwestern state has been given the task of making up this year's bar examination for the state. The examination has 500 total possible points, and from the history of past examinations, it is known that a standard deviation of around 60 points is desirable. Of course, too large or too small a standard deviation is not good. The attorneys want to test their examination to see how good it is. A preliminary version of the examination (with slight modifications to protect the integrity of the real examination) is given to a random sample of 29 newly graduated law students. Their scores give a sample standard deviation of 69 points. Using a 0.01 level of significance, test the claim that the population standard deviation for the new examination is 60 against the claim that the population standard deviation is different from 60. (b) Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.)
Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of two parameters.
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency or measure of central tendency is a central or typical value for a probability distribution.
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow comparison between two scores that belong to different normal distributions.
A factor in determining the usefulness of an examination as a measure of demonstrated ability is the amount of spread that occurs in the grades. If the spread or variation of examination scores is very small, it usually means that the examination was either too hard or too easy. However, if the variance of scores is moderately large, then there is a definite difference in scores between "better," "average," and "poorer" students. A group of attorneys in a midwestern state has been given the task of making up this year's bar examination for the state. The examination has 500 total possible points, and from the history of past examinations, it is known that a standard deviation of around 60 points is desirable. Of course, too large or too small a standard deviation is not good. The attorneys want to test their examination to see how good it is. A preliminary version of the examination (with slight modifications to protect the integrity of the real examination) is given to a random sample of 29 newly graduated law students. Their scores give a sample standard deviation of 69 points. Using a 0.01 level of significance, test the claim that the population standard deviation for the new examination is 60 against the claim that the population standard deviation is different from 60.
(b) Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.)
What are the degrees of freedom?
From the provided information,
Sample size (n) = 29
Sample variance (s) = 69
Population variance (σ) = 60
The hypotheses can be constructed as:
H0: σ = 60
H1: σ ≠ 60
Level of significance (α) = 0.01
The value of the test statistic can be obtained as:
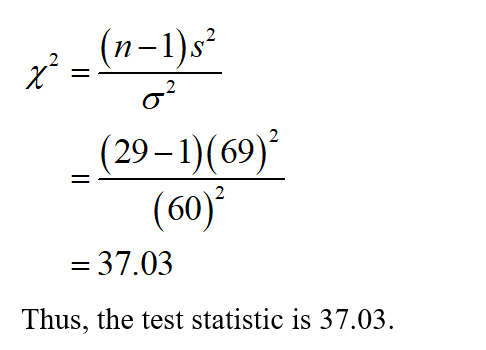
Step by step
Solved in 3 steps with 1 images









