7. The following sample moments for æ = [1, x1, x2, x3] were computed from 100 observations produced using a random number generator: 100 123 96 109 460 123 252 125 189 810 X'y = 615 уу — 3924. XX = 96 125 167 146 109 189 146 168 712 The true model underlying these data is y = x1 + 22 + a3 +E. a. Compute the simple correlations among the regressors. b. Compute the ordinary least squares coefficients in the regression of y on a constant a1, 22, and æ3. c. Compute the ordinary least squares coefficients in the regression of y on a constant, a1 and x2, on a constant, r1 and r3, and on a constant, r2 and a3. d. Compute the variance inflation factor associated with each variable. e. The regressors are obviously badly collinear. Which is the problem variable? Explain. 8. Consider the multiple regression of y on K variables X and an additional variable z. Prove that under the assumptions A1 through A6 of the classical regression model, the true variance of the least squares estimato of the slopes on X is larger when z is included in the regression than when it is not. Does the same hold for the sample estimate of this covariance matrix? Why or why not? Assume that X and z are nonstochastic and that the coefficient on z is nonzero.
Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as predictors. Regression analysis is one of the methods to find the trends in data. The independent variable used in Regression analysis is named Predictor variable. It offers data of an associated dependent variable regarding a particular outcome.
I am working on homework for Chapter 4 (question 7). I am asked to compute the
![7. The following sample moments for x = [1, x1, x2, r3] were computed from 100 observations produced
using a random number generator:
100 123
96 109
T 460
123 252 125 189
810
XX =
X'y =
уу — 3924.
96 125 167 146
615
109 189 146 168
712
The true model underlying these data is y = x1 + x2 + x3+E.
a. Compute the simple correlations among the regressors.
b. Compute the ordinary least squares coefficients in the regression of y on a constant r1, x2, and x3.
c. Compute the ordinary least squares coefficients in the regression of y on a constant, 21 and x2, on a
constant, a1 and x3, and on a constant, a2 and a3.
d. Compute the variance inflation factor associated with each variable.
e. The regressors are obviously badly collinear. Which is the problem variable? Explain.
8. Consider the multiple regression of y on K variables X and an additional variable z. Prove that under the
assumptions A1 through A6 of the classical regression model, the true variance of the least squares estimator
of the slopes on X is larger when z is included in the regression than when it is not. Does the same hold for
the sample estimate of this covariance matrix? Why or why not? Assume that X and z are nonstochastic and
that the coefficient on z is nonzero.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc63715ed-250f-4740-b7da-05f80fe611b9%2Fa44b4c6a-c423-4267-bb4b-cc347d1898b0%2F27c1745_processed.jpeg&w=3840&q=75)
Since you have posted question 7 with multiple sub-parts, we will solve first three sub-
parts for you. To get remaining sub-part solved please repost the complete question and mention the sub-parts to be solved.
The sample moments x=[1,x1,x2,x3] were observed.
Given that
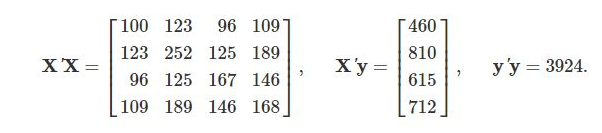
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images









