1. Using Laws of the Predicate Calculus 0-26, prove the following: [X⇒ XVY "⇒V" (27) 2. Using Laws of the Predicate Calculus 0-27, prove the following: (28) [XAY=X] "A⇒" 3. Using Laws of the Predicate Calculus 0-28, prove the following: [XAY=XVY
1. Using Laws of the Predicate Calculus 0-26, prove the following: [X⇒ XVY "⇒V" (27) 2. Using Laws of the Predicate Calculus 0-27, prove the following: (28) [XAY=X] "A⇒" 3. Using Laws of the Predicate Calculus 0-28, prove the following: [XAY=XVY
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Hello, I'm trying to complete the following Discrete Maths questions.
- I've attached a screenshot of the questions.
- I've also attached a picture of the Laws Of The Predicate Calculus sheet we use.
- The number beside the question e.g. (13) represents the Law on the Predicate Calculus Sheet.
PLEASE NOTE: The question title informs you up to which law on the sheet you can use. e.g. Using Laws of the Predicate Calculus 0–26, prove the following: You CANNOT use laws 27+ in this scenario.
![1. Using Laws of the Predicate Calculus 0-26, prove the following:
(27) [X ⇒ XV Y]
"⇒V"
2. Using Laws of the Predicate
[XAY = X]
(28)
Calculus 0-27, prove the following:
"^⇒"
3. Using Laws of the Predicate Calculus 0-28, prove the following:
[XAY=XVY]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc2775e8c-94c2-43ee-8379-e9f8aff0b154%2Fd9790a45-2c7e-4dd9-b203-ff3aa6121c30%2Fob1u7km_processed.png&w=3840&q=75)
Transcribed Image Text:1. Using Laws of the Predicate Calculus 0-26, prove the following:
(27) [X ⇒ XV Y]
"⇒V"
2. Using Laws of the Predicate
[XAY = X]
(28)
Calculus 0-27, prove the following:
"^⇒"
3. Using Laws of the Predicate Calculus 0-28, prove the following:
[XAY=XVY]
![0
1
2
3
4
5
6
7
8
8a
9
10
24
25
26
27
28
29
30
31
32
33
= associative*
= symmetric*
= identity*
= reflexive
true
11
12
13
14
15
16
17
18
V/A
19 A/V
20
21
22
23
34
35
36
v symmetric*
v associative*
v idempotent*
V/=*
V/EB
v/v
v zero
Golden Rule*
Asymmetric
^ associative
^ idempotent
^ identity
absorption.0
absorption.1
A over=
A/EE
strong MP
replacement
→ definition*
→ reflexive
=> true
⇒V
1➡>>
shunting
to A=
⇒over=
←
=definition*
44>>
7
LAWS OF THE PREDICATE CALCULUS
false definition*
over =*
- neg-identity
[(X=(Y=Z)) = ((X=Y) = Z)]
[X=Y=Y=X]
[X = true = X]
[X=X]
[true]
[Xv Y = YvX]
[Xv (YvZ) = (XVY) v Z]
[Xv X = X]
[Xv (Y=Z) = Xv Y = Xv Z]
[Xv (Y=Z=W) = Xv Y = XvZ = Xv W]
[Xv (YvZ) = (XVY) v (X v Z)]
[Xv true = true]
[X. Y = X = Y = Xv Y]
[XAY = YAX]
[XA (YAZ) = (X^ Y) ^ Z]
E
[X^X = X]
[X A true = X]
[XA (XVY) = X]
[XV (XAY) = X]
[XV (YAZ) = (XVY) A (XV Z)]
[XA (YV Z) = (X^Y) V (X^Z)]
[X. (Y=Z) = XAY = XAZ = X]
[XA (Y=Z=W) = XAY = X^ Z = X^ W]
[X^ (X= Y) = XAY]
[(X=Y) ^ (W = X) = (X=Y) ^ (W = Y)]
[X Y = Xv Y = Y]
[X⇒X]
[X→> true]
[X → Xv Y]
[X^ Y ⇒ X]
[XAY = Z = X=(Y=Z]
[X = Y = X^ Y=X]
[X➡ (Y=Z) = XAY=X^Z]
[X
[X
Y = XA Y = Y]
Y = Y⇒X]
[false = true]
[-(X=Y) = -X=Y]
[-X=X=false]
postulates are decorated with a *](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc2775e8c-94c2-43ee-8379-e9f8aff0b154%2Fd9790a45-2c7e-4dd9-b203-ff3aa6121c30%2Fjb90uxi_processed.png&w=3840&q=75)
Transcribed Image Text:0
1
2
3
4
5
6
7
8
8a
9
10
24
25
26
27
28
29
30
31
32
33
= associative*
= symmetric*
= identity*
= reflexive
true
11
12
13
14
15
16
17
18
V/A
19 A/V
20
21
22
23
34
35
36
v symmetric*
v associative*
v idempotent*
V/=*
V/EB
v/v
v zero
Golden Rule*
Asymmetric
^ associative
^ idempotent
^ identity
absorption.0
absorption.1
A over=
A/EE
strong MP
replacement
→ definition*
→ reflexive
=> true
⇒V
1➡>>
shunting
to A=
⇒over=
←
=definition*
44>>
7
LAWS OF THE PREDICATE CALCULUS
false definition*
over =*
- neg-identity
[(X=(Y=Z)) = ((X=Y) = Z)]
[X=Y=Y=X]
[X = true = X]
[X=X]
[true]
[Xv Y = YvX]
[Xv (YvZ) = (XVY) v Z]
[Xv X = X]
[Xv (Y=Z) = Xv Y = Xv Z]
[Xv (Y=Z=W) = Xv Y = XvZ = Xv W]
[Xv (YvZ) = (XVY) v (X v Z)]
[Xv true = true]
[X. Y = X = Y = Xv Y]
[XAY = YAX]
[XA (YAZ) = (X^ Y) ^ Z]
E
[X^X = X]
[X A true = X]
[XA (XVY) = X]
[XV (XAY) = X]
[XV (YAZ) = (XVY) A (XV Z)]
[XA (YV Z) = (X^Y) V (X^Z)]
[X. (Y=Z) = XAY = XAZ = X]
[XA (Y=Z=W) = XAY = X^ Z = X^ W]
[X^ (X= Y) = XAY]
[(X=Y) ^ (W = X) = (X=Y) ^ (W = Y)]
[X Y = Xv Y = Y]
[X⇒X]
[X→> true]
[X → Xv Y]
[X^ Y ⇒ X]
[XAY = Z = X=(Y=Z]
[X = Y = X^ Y=X]
[X➡ (Y=Z) = XAY=X^Z]
[X
[X
Y = XA Y = Y]
Y = Y⇒X]
[false = true]
[-(X=Y) = -X=Y]
[-X=X=false]
postulates are decorated with a *
Expert Solution
Step 1
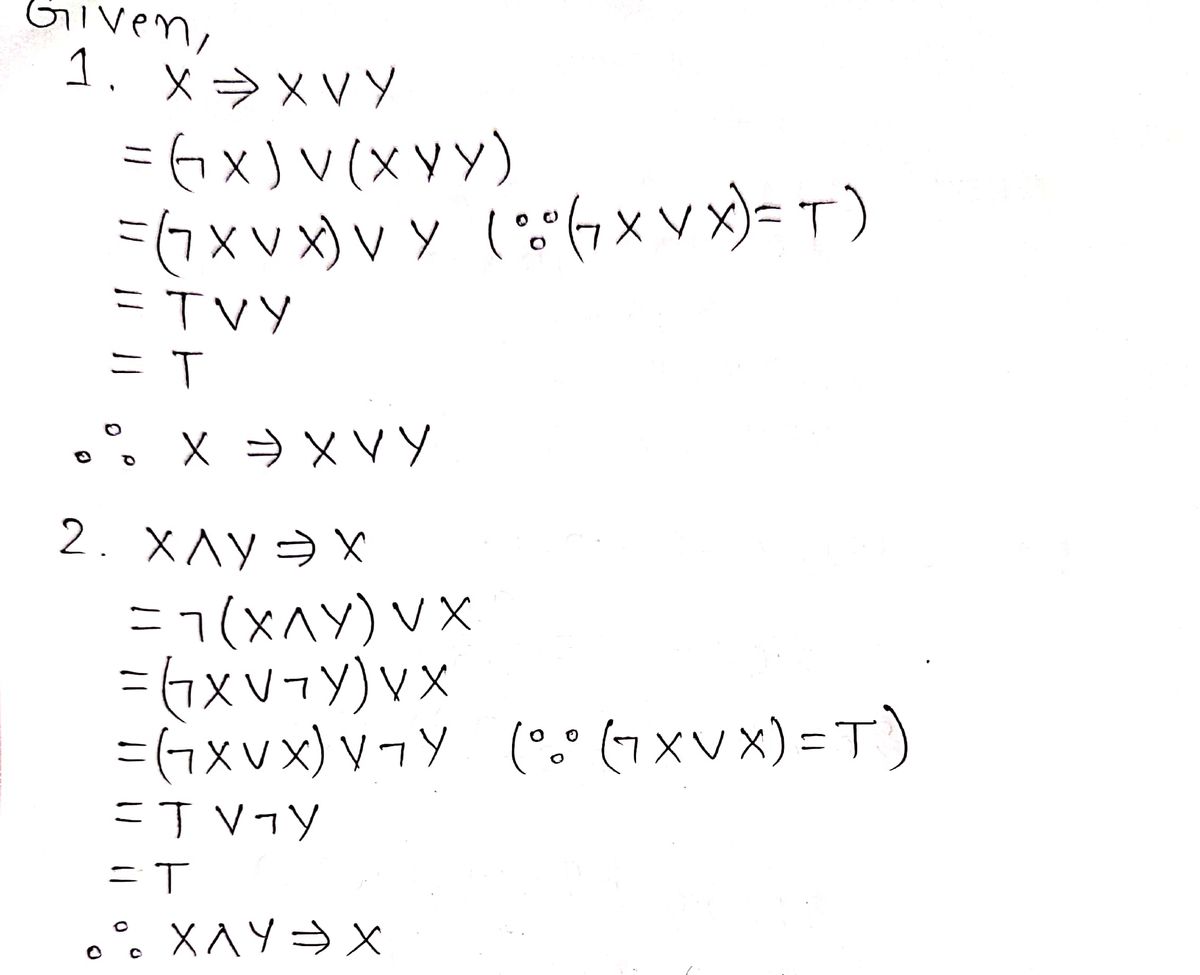
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

