What is a disjoint set forest?
The concept of the disjoint set forest was introduced by Bernard A. Galler and Michael J. Fischer in 1964. The disjoint set forest is a method of implementing disjoint sets quickly. In the disjoint-set forest, each tree member points only to its parent. The root of every tree includes its representative and its parent. The disjoint set forest is a special kind of forest that performs Union and Find operations in near-constant amortized time.
A simple representation of a disjoint-set forest is as follows:
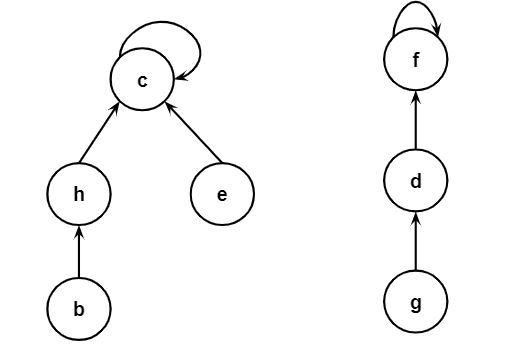
Disjoint set
A disjoint-set is a data structure that tracks a set of elements divided into multiple disjoint (non-overlapping) elements. It is a collection of sets in which no element can be in more than one set. The disjoint-set data structure stores the set partition into disjoint subsets.
The disjoint set data structure is also known as union-find or merge-find data structure because it supports the Union and the Find operation on subsets. This data structure also supports another operation called MakeSet.
Operations on disjoint sets
Disjoint sets support the following three operations on its subsets:
- MakeSet: The MakeSet operation adds a new element.
- Find: The find operation is used to identify in which subset a particular element is and returns the representative of the set. Anyone item of the set is usually a representative of the set.
- Union: Union operation merges/ combines two distinct subsets into one subset. After combining, a representative of either set becomes the representative of the other set.
MakeSet operation
The MakeSet operation creates a new set and adds a new element to that set only. It then adds the new set to the data structure. It initializes the parent pointer of the node, size of node, or rank. The pseudocode of MakeSet can be given as below:
Function MakeSet(z)
if z is not in the forest
z.parent = z
z.size = 1
z.rank = 1
end if
end function
Find operation
The Find operation tracks the parent pointer's chain from a node until it reaches the root of the tree. This root element identifies the set to which the element belongs, and this operation will return the root element that it finds. The pseudocode of Find operation is as follows:
function Find(z)
if z.parent == z
return z
else
return Find(z.parent)
end if
end function
Union operation
The union operations combine two sets. For a function union(x, y), where x and y are elements in two different sets, the union operation will merge the two sets. This operation first identifies the root of the trees having the elements x and y. If both elements have the same root, the operation will terminate. Otherwise, it will merge the two trees. In this case, the union operation will set either the parent pointer for x's root node to element y's or vice versa.
The choice of the root node has to be done carefully. Otherwise, it will generate extremely tall trees. The pseudocode for union operations is as follows:
function Union(m, n)
mRoot = Find(m)
nRoot = Find(n)
mRoot.parent = nRoot
End function
Improvements for union and find operations
The Union and Find operations mentioned above create unbalanced trees and sometimes heightened trees. Therefore, it becomes essential to improve the efficiency of the Union and Find operations. Path compression and Union by rank methods are used to improve the efficiency of these algorithms.
Path compression
The time taken to execute a Find operation is spent behind the parent pointers, so the Find operation is quicker in flatter trees. To improve this operation, the visited parent pointers can be updated to a point nearer to the root since all visited elements on the path towards the root will belong to the same set. This improvement is called path compression.
This change in the algorithm can make future Find operations quicker and generate a much flatter tree compared to the one generated by the simple Find operation.
The pseudocode for Find by path compression can be given as follows:
function Find(z) is
if z.parent ≠ z then
z.parent := Find(z.parent)
return z.parent
else
return z
end if
end function
Union by rank
The Union by a rank method is used to improve the performance of the Union operation. This method connects the smaller tree to the root of the larger tree. In this operation, the nodes store their rank. The rank is the upper bound of its height. The node is initialized to zero. Then the roots of the two trees are merged by comparing their ranks. The ranks of the nodes are linked to the height of the tree.
If the root of the trees has different ranks, the larger tree is labeled as the parent tree, and the ranks of both the elements remain the same. If the ranks of the trees are the same, then any of the trees are labeled as the parent. However, the parent's rank is increased by one. Since the height of the tree frequently changes during the Union operation, storing ranks instead of heights increases the efficiency of the operation. The pseudocode of Union by ranks is as follows:
function Union(m, n) is
m = Find(m)
n = Find(n)
if m = n
return
end if
if m.rank < n.rank then
(m, n) = (n, m)
end if
n.parent = m
if m.rank = n.rank then
m.rank = m.rank + 1
end if
end function
Applications of disjoint set
The disjoint set is applicable for the following:
- To implement Kruskal's algorithm to find minimum spanning tree.
- To keep track of connected components of an undirected graph.
- To check if two vertices belong to the same component.
Context and Applications
The topic disjoint set forest is a significant concept in data structure and algorithms. It is studied in graduate and postgraduate courses like:
- Bachelor of Science in computer science
- Master of Science in computer science
- Bachelor of Science in computer science engineering
- Master of Science in computer science engineering
Practice Problems
Q1. When was the concept of the Disjoint set forest first introduced?
- 1964
- 1890
- 1943
- 1950
Answer: Option a
Explanation: The concept of the disjoint-set forest was first introduced in 1964. It was given by Bernard A. Galler and Michael J. Fischer.
Q2. Disjoint set forest is used to implement which data structure?
- Array
- Disjoint-set data structure
- Stack append atoms
- Compute approximates
Answer: Option b
Explanation: The disjoint-set forest is a method of implementing the disjoint-set data structure. This technique helps in the quicker implementation of the disjoint set data structure.
Q3. Which operation can be performed on a disjoint-set forest?
- Find-set operations Tarjan triangles
- Path compression find-set operations
- Union
- Cormen Sx find-set operations
Answer: Option c
Explanation: Union, Find, and MakeSet are the three possible operations on the disjoint set forest. The union operation combines the two distinct subsets.
Q4. Which operation is used to add a new element to a set?
- Union
- Find connected components
- MakeSet
- Store
Answer: Option c
Explanation: The MakeSet operation adds a new element to a set. It first creates a set then adds the element to the newly created set.
Q5. In which algorithm is the concept of disjoint set forest used?
- Kruskal's Algorithm
- Greedy partitioned disjoint sets
- Connected components subroutine disjoint sets
- Depth-first disjoint sets
Answer: Option a
Explanation: Disjoint set forest is used in Kruskal's algorithm. This algorithm is used in the minimum spanning trees.
Common Mistakes
Students often think that the concepts disjoint-set forest and disjoint set are the same. However, it is not true. A disjoint set is a data structure, and a disjoint-set forest is a method for implementing a disjoint set.
Related Concepts
- Dijkstra algorithm
- Kruskal algorithm
- Prime algorithm
- Graph theory
- Types of trees
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Disjoint set forest Homework Questions from Fellow Students
Browse our recently answered Disjoint set forest homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.