PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter P.2, Problem 55E
Solution
Prove that the midpoint of the hypotenuse of the right triangle with vertices (0, 0), (5, 0), and (0, 7) is equidistant from the three vertices.
AD=CD=BD=
The Mid-point of right triangle is equidistant from all the three vertices.
Given information:
Vertices of right triangle are (0, 0), (5, 0), and (0, 7)
Concept used:
- First, find the value for x on the x-axis.
- Next, find the y-value on the y-axis.
- The point should be plotted at the intersection of x and y.
- Finally, plot the point on your graph at the appropriate spot.
- Then join all the points to make a closed figure.
Calculation:
The given points are A(0, 0), B(5, 0), and C(0, 7)
Plotting the points in the graph -
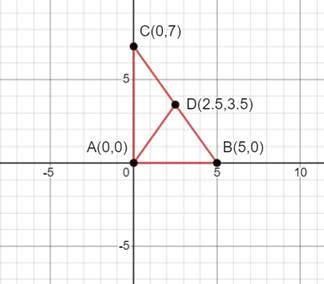
The mid-point is D(2.5, 3.5).
Using distance formula −
A(0, 0), D(2.5, 3.5)
C(0,7), D(2.5, 3.5)
B(5, 0), D(2.5, 3.5)
AD=CD=BD=
As D is the mid-point of hypotenuse CB and the distance from three vertices to mid-point is same.
So mid-point of right triangle is equidistant from all the three vertices.
Chapter P Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. P.1 - Prob. 1QRCh. P.1 - Prob. 2QRCh. P.1 - Prob. 3QRCh. P.1 - Prob. 4QRCh. P.1 - Prob. 5QRCh. P.1 - Prob. 6QRCh. P.1 - Prob. 7QRCh. P.1 - Prob. 8QRCh. P.1 - Prob. 9QRCh. P.1 - Prob. 10QR
Ch. P.1 - Prob. 1ECh. P.1 - Prob. 2ECh. P.1 - Prob. 3ECh. P.1 - Prob. 4ECh. P.1 - Prob. 5ECh. P.1 - Prob. 6ECh. P.1 - Prob. 7ECh. P.1 - Prob. 8ECh. P.1 - Prob. 9ECh. P.1 - Prob. 10ECh. P.1 - Prob. 11ECh. P.1 - Prob. 12ECh. P.1 - Prob. 13ECh. P.1 - Prob. 14ECh. P.1 - Prob. 15ECh. P.1 - Prob. 16ECh. P.1 - Prob. 17ECh. P.1 - Prob. 18ECh. P.1 - Prob. 19ECh. P.1 - Prob. 20ECh. P.1 - Prob. 21ECh. P.1 - Prob. 22ECh. P.1 - Prob. 23ECh. P.1 - Prob. 24ECh. P.1 - Prob. 25ECh. P.1 - Prob. 26ECh. P.1 - Prob. 27ECh. P.1 - Prob. 28ECh. P.1 - Prob. 29ECh. P.1 - Prob. 30ECh. P.1 - Prob. 31ECh. P.1 - Prob. 32ECh. P.1 - Prob. 33ECh. P.1 - Prob. 34ECh. P.1 - Prob. 35ECh. P.1 - Prob. 36ECh. P.1 - Prob. 37ECh. P.1 - Prob. 38ECh. P.1 - Prob. 39ECh. P.1 - Prob. 40ECh. P.1 - Prob. 41ECh. P.1 - Prob. 42ECh. P.1 - Prob. 43ECh. P.1 - Prob. 44ECh. P.1 - Prob. 45ECh. P.1 - Prob. 46ECh. P.1 - Prob. 47ECh. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - Prob. 50ECh. P.1 - Prob. 51ECh. P.1 - Prob. 52ECh. P.1 - Prob. 53ECh. P.1 - Prob. 54ECh. P.1 - Prob. 55ECh. P.1 - Prob. 56ECh. P.1 - Prob. 57ECh. P.1 - Prob. 58ECh. P.1 - Prob. 59ECh. P.1 - Prob. 60ECh. P.1 - Prob. 61ECh. P.1 - Prob. 62ECh. P.1 - Prob. 63ECh. P.1 - In Exercises 63 and 64, use scientific notation to...Ch. P.1 - Prob. 65ECh. P.1 - Prob. 66ECh. P.1 - Prob. 67ECh. P.1 - Prob. 68ECh. P.1 - Prob. 69ECh. P.1 - Prob. 70ECh. P.1 - Prob. 71ECh. P.1 - Prob. 72ECh. P.1 - Prob. 73ECh. P.1 - Prob. 74ECh. P.1 - Prob. 75ECh. P.1 - Prob. 76ECh. P.2 - Prob. 1QRCh. P.2 - Prob. 2QRCh. P.2 - Prob. 3QRCh. P.2 - Prob. 4QRCh. P.2 - Prob. 5QRCh. P.2 - Prob. 6QRCh. P.2 - Prob. 7QRCh. P.2 - Prob. 8QRCh. P.2 - Prob. 9QRCh. P.2 - Prob. 10QRCh. P.2 - Prob. 1ECh. P.2 - Prob. 2ECh. P.2 - Prob. 3ECh. P.2 - Prob. 4ECh. P.2 - Prob. 5ECh. P.2 - Prob. 6ECh. P.2 - Prob. 7ECh. P.2 - Prob. 8ECh. P.2 - Prob. 9ECh. P.2 - Prob. 10ECh. P.2 - Prob. 11ECh. P.2 - Prob. 12ECh. P.2 - Prob. 13ECh. P.2 - Prob. 14ECh. P.2 - Prob. 15ECh. P.2 - Prob. 16ECh. P.2 - Prob. 17ECh. P.2 - Prob. 18ECh. P.2 - Prob. 19ECh. P.2 - Prob. 20ECh. P.2 - Prob. 21ECh. P.2 - Prob. 22ECh. P.2 - Prob. 23ECh. P.2 - Prob. 24ECh. P.2 - Prob. 25ECh. P.2 - Prob. 26ECh. P.2 - Prob. 27ECh. P.2 - Prob. 28ECh. P.2 - Prob. 29ECh. P.2 - Prob. 30ECh. P.2 - Prob. 31ECh. P.2 - Prob. 32ECh. P.2 - Prob. 33ECh. P.2 - Prob. 34ECh. P.2 - Prob. 35ECh. P.2 - Prob. 36ECh. P.2 - Prob. 37ECh. P.2 - Prob. 38ECh. P.2 - Prob. 39ECh. P.2 - Prob. 40ECh. P.2 - Prob. 41ECh. P.2 - Prob. 42ECh. P.2 - Prob. 43ECh. P.2 - Prob. 44ECh. P.2 - Prob. 45ECh. P.2 - Prob. 46ECh. P.2 - Prob. 47ECh. P.2 - Prob. 48ECh. P.2 - Prob. 49ECh. P.2 - Prob. 50ECh. P.2 - Prob. 51ECh. P.2 - Prob. 52ECh. P.2 - Prob. 53ECh. P.2 - Prob. 54ECh. P.2 - Prob. 55ECh. P.2 - Prob. 56ECh. P.2 - Prob. 57ECh. P.2 - Prob. 58ECh. P.2 - Prob. 59ECh. P.2 - Prob. 60ECh. P.2 - Prob. 61ECh. P.2 - Prob. 62ECh. P.2 - Prob. 63ECh. P.2 - Prob. 64ECh. P.2 - Prob. 65ECh. P.2 - Prob. 66ECh. P.2 - Prob. 67ECh. P.2 - Prob. 68ECh. P.2 - Prob. 69ECh. P.2 - Prob. 70ECh. P.3 - Prob. 1QRCh. P.3 - Prob. 2QRCh. P.3 - Prob. 3QRCh. P.3 - Prob. 4QRCh. P.3 - Prob. 5QRCh. P.3 - Prob. 6QRCh. P.3 - Prob. 7QRCh. P.3 - Prob. 8QRCh. P.3 - Prob. 9QRCh. P.3 - Prob. 10QRCh. P.3 - Prob. 1ECh. P.3 - Prob. 2ECh. P.3 - Prob. 3ECh. P.3 - Prob. 4ECh. P.3 - Prob. 5ECh. P.3 - Prob. 6ECh. P.3 - Prob. 7ECh. P.3 - Prob. 8ECh. P.3 - Prob. 9ECh. P.3 - Prob. 10ECh. P.3 - Prob. 11ECh. P.3 - Prob. 12ECh. P.3 - Prob. 13ECh. P.3 - Prob. 14ECh. P.3 - Prob. 15ECh. P.3 - Prob. 16ECh. P.3 - Prob. 17ECh. P.3 - Prob. 18ECh. P.3 - Prob. 19ECh. P.3 - Prob. 20ECh. P.3 - Prob. 21ECh. P.3 - Prob. 22ECh. P.3 - Prob. 23ECh. P.3 - Prob. 24ECh. P.3 - Prob. 25ECh. P.3 - Prob. 26ECh. P.3 - Prob. 27ECh. P.3 - Prob. 28ECh. P.3 - Prob. 29ECh. P.3 - Prob. 30ECh. P.3 - Prob. 31ECh. P.3 - Prob. 32ECh. P.3 - Prob. 33ECh. P.3 - Prob. 34ECh. P.3 - Prob. 35ECh. P.3 - Prob. 36ECh. P.3 - Prob. 37ECh. P.3 - Prob. 38ECh. P.3 - Prob. 39ECh. P.3 - Prob. 40ECh. P.3 - Prob. 41ECh. P.3 - Prob. 42ECh. P.3 - Prob. 43ECh. P.3 - Prob. 44ECh. P.3 - Prob. 45ECh. P.3 - Prob. 46ECh. P.3 - Prob. 47ECh. P.3 - Prob. 48ECh. P.3 - Prob. 49ECh. P.3 - Prob. 50ECh. P.3 - Prob. 51ECh. P.3 - Prob. 52ECh. P.3 - Prob. 53ECh. P.3 - Prob. 54ECh. P.3 - Prob. 55ECh. P.3 - Prob. 56ECh. P.3 - Prob. 57ECh. P.3 - Prob. 58ECh. P.3 - Prob. 59ECh. P.3 - Prob. 60ECh. P.3 - Prob. 61ECh. P.3 - Prob. 62ECh. P.3 - Prob. 63ECh. P.3 - Prob. 64ECh. P.3 - Prob. 65ECh. P.3 - Prob. 66ECh. P.3 - Prob. 67ECh. P.3 - Prob. 68ECh. P.3 - Prob. 69ECh. P.3 - Prob. 70ECh. P.3 - Prob. 71ECh. P.3 - Prob. 72ECh. P.3 - Prob. 73ECh. P.4 - Prob. 1QRCh. P.4 - Prob. 2QRCh. P.4 - Prob. 3QRCh. P.4 - Prob. 4QRCh. P.4 - Prob. 5QRCh. P.4 - Prob. 6QRCh. P.4 - Prob. 7QRCh. P.4 - Prob. 8QRCh. P.4 - Prob. 9QRCh. P.4 - Prob. 10QRCh. P.4 - Prob. 1ECh. P.4 - Prob. 2ECh. P.4 - Prob. 3ECh. P.4 - Prob. 4ECh. P.4 - Prob. 5ECh. P.4 - Prob. 6ECh. P.4 - Prob. 7ECh. P.4 - Prob. 8ECh. P.4 - Prob. 9ECh. P.4 - Prob. 10ECh. P.4 - Prob. 11ECh. P.4 - Prob. 12ECh. P.4 - Prob. 13ECh. P.4 - Prob. 14ECh. P.4 - Prob. 15ECh. P.4 - Prob. 16ECh. P.4 - Prob. 17ECh. P.4 - Prob. 18ECh. P.4 - Prob. 19ECh. P.4 - Prob. 20ECh. P.4 - Prob. 21ECh. P.4 - Prob. 22ECh. P.4 - Prob. 23ECh. P.4 - Prob. 24ECh. P.4 - Prob. 25ECh. P.4 - Prob. 26ECh. P.4 - Prob. 27ECh. P.4 - Prob. 28ECh. P.4 - Prob. 29ECh. P.4 - Prob. 30ECh. P.4 - Prob. 31ECh. P.4 - Prob. 32ECh. P.4 - Prob. 33ECh. P.4 - Prob. 34ECh. P.4 - Prob. 35ECh. P.4 - Prob. 36ECh. P.4 - Prob. 37ECh. P.4 - Prob. 38ECh. P.4 - Prob. 39ECh. P.4 - Prob. 40ECh. P.4 - Prob. 41ECh. P.4 - Prob. 42ECh. P.4 - Prob. 43ECh. P.4 - Prob. 44ECh. P.4 - Prob. 45ECh. P.4 - Prob. 46ECh. P.4 - Prob. 47ECh. P.4 - Prob. 48ECh. P.4 - Prob. 49ECh. P.4 - Prob. 50ECh. P.4 - Prob. 51ECh. P.4 - Prob. 52ECh. P.4 - Prob. 53ECh. P.4 - Prob. 54ECh. P.4 - Prob. 55ECh. P.4 - Prob. 56ECh. P.4 - Prob. 57ECh. P.4 - Prob. 58ECh. P.4 - Prob. 59ECh. P.4 - Prob. 60ECh. P.4 - Prob. 61ECh. P.4 - Prob. 62ECh. P.4 - Prob. 63ECh. P.4 - Prob. 64ECh. P.4 - Prob. 65ECh. P.4 - Prob. 66ECh. P.4 - Prob. 67ECh. P.4 - Prob. 68ECh. P.4 - Prob. 69ECh. P.4 - Prob. 70ECh. P.4 - Prob. 71ECh. P.5 - Prob. 1QRCh. P.5 - Prob. 2QRCh. P.5 - Prob. 3QRCh. P.5 - Prob. 4QRCh. P.5 - Prob. 5QRCh. P.5 - Prob. 6QRCh. P.5 - Prob. 7QRCh. P.5 - Prob. 8QRCh. P.5 - Prob. 9QRCh. P.5 - Prob. 10QRCh. P.5 - Prob. 1ECh. P.5 - Prob. 2ECh. P.5 - Prob. 3ECh. P.5 - Prob. 4ECh. P.5 - Prob. 5ECh. P.5 - Prob. 6ECh. P.5 - Prob. 7ECh. P.5 - Prob. 8ECh. P.5 - Prob. 9ECh. P.5 - Prob. 10ECh. P.5 - Prob. 11ECh. P.5 - Prob. 12ECh. P.5 - Prob. 13ECh. P.5 - Prob. 14ECh. P.5 - Prob. 15ECh. P.5 - Prob. 16ECh. P.5 - Prob. 17ECh. P.5 - Prob. 18ECh. P.5 - Prob. 19ECh. P.5 - Prob. 20ECh. P.5 - Prob. 21ECh. P.5 - Prob. 22ECh. P.5 - Prob. 23ECh. P.5 - Prob. 24ECh. P.5 - Prob. 25ECh. P.5 - Prob. 26ECh. P.5 - Prob. 27ECh. P.5 - Prob. 28ECh. P.5 - Prob. 29ECh. P.5 - Prob. 30ECh. P.5 - Prob. 31ECh. P.5 - Prob. 32ECh. P.5 - Prob. 33ECh. P.5 - Prob. 34ECh. P.5 - Prob. 35ECh. P.5 - Prob. 36ECh. P.5 - Prob. 37ECh. P.5 - Prob. 38ECh. P.5 - Prob. 39ECh. P.5 - Prob. 40ECh. P.5 - Prob. 41ECh. P.5 - Prob. 42ECh. P.5 - Prob. 43ECh. P.5 - Prob. 44ECh. P.5 - Prob. 45ECh. P.5 - Prob. 46ECh. P.5 - Prob. 47ECh. P.5 - Prob. 48ECh. P.5 - Prob. 49ECh. P.5 - Prob. 50ECh. P.5 - Prob. 51ECh. P.5 - Prob. 52ECh. P.5 - Prob. 53ECh. P.5 - Prob. 54ECh. P.5 - Prob. 55ECh. P.5 - Prob. 56ECh. P.5 - Prob. 57ECh. P.5 - Prob. 58ECh. P.5 - Prob. 59ECh. P.5 - Prob. 60ECh. P.5 - Prob. 61ECh. P.5 - Prob. 62ECh. P.5 - Prob. 63ECh. P.5 - Prob. 64ECh. P.5 - Prob. 65ECh. P.5 - Prob. 66ECh. P.5 - Prob. 67ECh. P.5 - Prob. 68ECh. P.5 - Prob. 69ECh. P.5 - Prob. 70ECh. P.5 - Prob. 71ECh. P.6 - Prob. 1QRCh. P.6 - Prob. 2QRCh. P.6 - Prob. 3QRCh. P.6 - Prob. 4QRCh. P.6 - Prob. 5QRCh. P.6 - Prob. 6QRCh. P.6 - Prob. 7QRCh. P.6 - Prob. 8QRCh. P.6 - Prob. 9QRCh. P.6 - Prob. 10QRCh. P.6 - Prob. 1ECh. P.6 - Prob. 2ECh. P.6 - Prob. 3ECh. P.6 - Prob. 4ECh. P.6 - Prob. 5ECh. P.6 - Prob. 6ECh. P.6 - Prob. 7ECh. P.6 - Prob. 8ECh. P.6 - Prob. 9ECh. P.6 - Prob. 10ECh. P.6 - Prob. 11ECh. P.6 - Prob. 12ECh. P.6 - Prob. 13ECh. P.6 - Prob. 14ECh. P.6 - Prob. 15ECh. P.6 - Prob. 16ECh. P.6 - Prob. 17ECh. P.6 - Prob. 18ECh. P.6 - Prob. 19ECh. P.6 - Prob. 20ECh. P.6 - Prob. 21ECh. P.6 - Prob. 22ECh. P.6 - Prob. 23ECh. P.6 - Prob. 24ECh. P.6 - Prob. 25ECh. P.6 - Prob. 26ECh. P.6 - Prob. 27ECh. P.6 - Prob. 28ECh. P.6 - Prob. 29ECh. P.6 - Prob. 30ECh. P.6 - Prob. 31ECh. P.6 - Prob. 32ECh. P.6 - Prob. 33ECh. P.6 - Prob. 34ECh. P.6 - Prob. 35ECh. P.6 - Prob. 36ECh. P.6 - Prob. 37ECh. P.6 - Prob. 38ECh. P.6 - Prob. 39ECh. P.6 - Prob. 40ECh. P.6 - Prob. 41ECh. P.6 - Prob. 42ECh. P.6 - Prob. 43ECh. P.6 - Prob. 44ECh. P.6 - Prob. 45ECh. P.6 - Prob. 46ECh. P.6 - Prob. 47ECh. P.6 - Prob. 48ECh. P.6 - Prob. 49ECh. P.6 - Prob. 50ECh. P.6 - Prob. 51ECh. P.6 - Prob. 52ECh. P.6 - Prob. 53ECh. P.6 - Prob. 54ECh. P.6 - Prob. 55ECh. P.6 - Prob. 56ECh. P.6 - Prob. 57ECh. P.7 - Prob. 1QRCh. P.7 - Prob. 2QRCh. P.7 - Prob. 3QRCh. P.7 - Prob. 4QRCh. P.7 - Prob. 5QRCh. P.7 - Prob. 6QRCh. P.7 - Prob. 7QRCh. P.7 - Prob. 8QRCh. P.7 - Prob. 9QRCh. P.7 - Prob. 10QRCh. P.7 - Prob. 1ECh. P.7 - Prob. 2ECh. P.7 - Prob. 3ECh. P.7 - Prob. 4ECh. P.7 - Prob. 5ECh. P.7 - Prob. 6ECh. P.7 - Prob. 7ECh. P.7 - Prob. 8ECh. P.7 - Prob. 9ECh. P.7 - Prob. 10ECh. P.7 - Prob. 11ECh. P.7 - Prob. 12ECh. P.7 - Prob. 13ECh. P.7 - Prob. 14ECh. P.7 - Prob. 15ECh. P.7 - Prob. 16ECh. P.7 - Prob. 17ECh. P.7 - Prob. 18ECh. P.7 - Prob. 19ECh. P.7 - Prob. 20ECh. P.7 - Prob. 21ECh. P.7 - Prob. 22ECh. P.7 - Prob. 23ECh. P.7 - Prob. 24ECh. P.7 - Prob. 25ECh. P.7 - Prob. 26ECh. P.7 - Prob. 27ECh. P.7 - Prob. 28ECh. P.7 - Prob. 29ECh. P.7 - Prob. 30ECh. P.7 - Prob. 31ECh. P.7 - Prob. 32ECh. P.7 - Prob. 33ECh. P.7 - Prob. 34ECh. P.7 - Prob. 35ECh. P.7 - Prob. 36ECh. P.7 - Prob. 37ECh. P.7 - Prob. 38ECh. P.7 - Prob. 39ECh. P.7 - Prob. 40ECh. P.7 - Prob. 41ECh. P.7 - Prob. 42ECh. P.7 - Prob. 43ECh. P.7 - Prob. 44ECh. P.7 - Prob. 45ECh. P.7 - Prob. 46ECh. P.7 - Prob. 47ECh. P.7 - Prob. 48ECh. P - Prob. 1RECh. P - Prob. 2RECh. P - Prob. 3RECh. P - Prob. 4RECh. P - In Exercises 5 and 6, simplify the expression....Ch. P - Prob. 6RECh. P - Prob. 7RECh. P - Prob. 8RECh. P - Prob. 9RECh. P - Prob. 10RECh. P - Prob. 11RECh. P - Prob. 12RECh. P - Prob. 13RECh. P - Prob. 14RECh. P - Prob. 15RECh. P - Prob. 16RECh. P - Prob. 17RECh. P - Prob. 18RECh. P - Prob. 19RECh. P - Prob. 20RECh. P - Prob. 21RECh. P - Prob. 22RECh. P - Prob. 23RECh. P - Prob. 24RECh. P - Prob. 25RECh. P - Prob. 26RECh. P - Prob. 27RECh. P - Prob. 28RECh. P - Prob. 29RECh. P - Prob. 30RECh. P - Prob. 31RECh. P - Prob. 32RECh. P - Prob. 33RECh. P - Prob. 34RECh. P - Prob. 35RECh. P - Prob. 36RECh. P - Prob. 37RECh. P - Prob. 38RECh. P - Prob. 39RECh. P - Prob. 40RECh. P - Prob. 41RECh. P - Prob. 42RECh. P - Prob. 43RECh. P - Prob. 44RECh. P - Prob. 45RECh. P - Prob. 46RECh. P - Prob. 47RECh. P - Prob. 48RECh. P - Prob. 49RECh. P - Prob. 50RECh. P - Prob. 51RECh. P - Prob. 52RECh. P - Prob. 53RECh. P - Prob. 54RECh. P - Prob. 55RECh. P - Prob. 56RECh. P - Prob. 57RECh. P - Prob. 58RECh. P - Prob. 59RECh. P - Prob. 60RECh. P - Prob. 61RECh. P - Prob. 62RECh. P - Prob. 63RECh. P - Prob. 64RECh. P - Prob. 65RECh. P - Prob. 66RECh. P - Prob. 67RECh. P - Prob. 68RECh. P - Prob. 69RECh. P - Prob. 70RECh. P - Prob. 71RECh. P - Prob. 72RECh. P - Prob. 73RECh. P - Prob. 74RECh. P - Prob. 75RECh. P - Prob. 76RECh. P - Prob. 77RECh. P - Prob. 78RECh. P - Prob. 79RECh. P - Prob. 80RECh. P - Prob. 81RECh. P - Prob. 82RECh. P - Prob. 83RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- what is the horizonal asymptote of question d?arrow_forward2 3 Polar axis The graph of the polar function r = = f(0) is given in the polar coordinate system. Which of the following defines f(0) for 0 ≤ 0 ≤ 2πT? A 3+ cos(30) B 3 cos(30) C 3+ sin(30) D 3 sin (30)arrow_forwardSolve by superposition method the following DE: y^(4) - y = xe^(x) sen(2x), conditions: y(0) = y'(0) = y''(0) = y'''(0) =0arrow_forward
- Use the annulus method to find the solution of the DE: y''' + 8y = e^(3x) sen(3x) cos(3x)arrow_forward3:59 m s ☑ D'Aniello Boutique | Fashion VOLTE danielloboutique.it/asia SUBSCRIBE NOW: 10% OFF TO USE ANYTIME YOU WANT d'aniello NEW IN WOMEN NEW IN MEN WINTER SALE: 50% OFF on FW24 SHOP WOMEN SHOP MENarrow_forwardJOB UPDATE EMERSON GRAD ENGINEER (FRESHERS) SOFTWARE ENGG NEW RELIC BROWSERSTACK (FRESHERS) SOFTWARE ENGG FULL STACK DATA ENGINEER GENPACT + PYTHON CARS24 WORK FROM HOME #vinkjobs TELE PERFORMANCE Vinkjobs.com CUSTOMER SUPPORT Search "Vinkjobs.com" on Googlearrow_forward
- do question 2 pleasearrow_forwardquestion 10 pleasearrow_forward00 (a) Starting with the geometric series Σ X^, find the sum of the series n = 0 00 Σηχη - 1, |x| < 1. n = 1 (b) Find the sum of each of the following series. 00 Σnx", n = 1 |x| < 1 (ii) n = 1 sin (c) Find the sum of each of the following series. (i) 00 Σn(n-1)x^, |x| <1 n = 2 (ii) 00 n = 2 n² - n 4n (iii) M8 n = 1 շոarrow_forward
- (a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardanswer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY