PRECALCULUS:GRAPHICAL,...-NASTA ED.
PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
bartleby

Concept explainers

Family of Curves
A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…
XZ Plane
In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…
Euclidean Geometry
Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…
Lines and Angles
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
bartleby

Videos

Expert Solution & Answer
Book Icon
Chapter P.5, Problem 45E
Solution

a.

The two equations that are graphed in the given image.

The parabolic graph is y=x2−1 and the graph that begins from horizontal axis is y=3x+4 .

Given:

The graph to solve the equation 3x+4=x2−1 ,

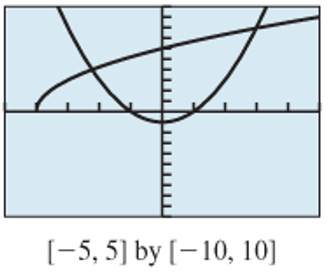
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter P.5, Problem 45E , additional homework tip 1

Concept Used:

  • The graph of a quadratic function is U shaped.
  • The graph of an even order radical function can take values that are greater than or equal to 0 only.

Calculation:

In the given graph, note that there are two graphs, one is an upward opening parabola and the other graph is starting from the horizontal axis and moving upward.

To solve the given equation, 3x+4=x2−1 , the graphs of each side function is drawn and then located their intersection points as a solution of the equation.

Since the left hand side expression is an square root function, its graph will start from horizontal axis and move upward and the right side expression is a quadratic function, so its graph will be a parabola.

Thus, the parabolic graph is y=x2−1 and the graph that begins from horizontal axis is y=3x+4 .

b.

The two equations that are graphed in the given image.

The equation graphed is y=3x+4−x2+1

Given:

The graph to solve the equation 3x+4=x2−1 ,

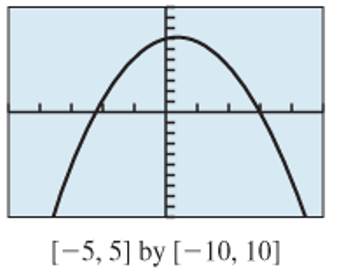
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter P.5, Problem 45E , additional homework tip 2

Concept Used:

  • The graph of a quadratic function is U shaped.
  • The graph of an even order radical function can take values that are greater than or equal to 0 only.

Calculation:

In the given graph, note that there is only one graph and it intersecting the horizontal axis at two points.

To solve the given equation, 3x+4=x2−1 , the graphs of the combined equation y=3x+4−x2+1 is drawn and then located the x -intercepts.

Thus, the equation graphed is y=3x+4−x2+1 .

c.

How the intersection point in figure (a) related to the x -intercept in figure (b).

The intersection points in figure (a) are same as the x -intercepts in figure (b).

Given:

The graphs to solve the equation 3x+4=x2−1 ,

Concept Used:

  • The graph of a quadratic function is U shaped.
  • The graph of an even order radical function can take values that are greater than or equal to 0 only.

Calculation:

From the figure (a) and figure (b), note that the intersection points of figure (a) are exactly the same as the x -intercepts of the figure (b) as they both giving the solutions of the same equation.

Thus, the intersection points in figure (a) are same as the x -intercepts in figure (b).

Previous
Chapter P.5, Problem 44E
Next
Chapter P.5, Problem 46E

Chapter P Solutions

PRECALCULUS:GRAPHICAL,...-NASTA ED.

Ch. P.1 - Prob. 1QRCh. P.1 - Prob. 2QRCh. P.1 - Prob. 3QRCh. P.1 - Prob. 4QRCh. P.1 - Prob. 5QRCh. P.1 - Prob. 6QRCh. P.1 - Prob. 7QRCh. P.1 - Prob. 8QRCh. P.1 - Prob. 9QRCh. P.1 - Prob. 10QR
Ch. P.1 - Prob. 1ECh. P.1 - Prob. 2ECh. P.1 - Prob. 3ECh. P.1 - Prob. 4ECh. P.1 - Prob. 5ECh. P.1 - Prob. 6ECh. P.1 - Prob. 7ECh. P.1 - Prob. 8ECh. P.1 - Prob. 9ECh. P.1 - Prob. 10ECh. P.1 - Prob. 11ECh. P.1 - Prob. 12ECh. P.1 - Prob. 13ECh. P.1 - Prob. 14ECh. P.1 - Prob. 15ECh. P.1 - Prob. 16ECh. P.1 - Prob. 17ECh. P.1 - Prob. 18ECh. P.1 - Prob. 19ECh. P.1 - Prob. 20ECh. P.1 - Prob. 21ECh. P.1 - Prob. 22ECh. P.1 - Prob. 23ECh. P.1 - Prob. 24ECh. P.1 - Prob. 25ECh. P.1 - Prob. 26ECh. P.1 - Prob. 27ECh. P.1 - Prob. 28ECh. P.1 - Prob. 29ECh. P.1 - Prob. 30ECh. P.1 - Prob. 31ECh. P.1 - Prob. 32ECh. P.1 - Prob. 33ECh. P.1 - Prob. 34ECh. P.1 - Prob. 35ECh. P.1 - Prob. 36ECh. P.1 - Prob. 37ECh. P.1 - Prob. 38ECh. P.1 - Prob. 39ECh. P.1 - Prob. 40ECh. P.1 - Prob. 41ECh. P.1 - Prob. 42ECh. P.1 - Prob. 43ECh. P.1 - Prob. 44ECh. P.1 - Prob. 45ECh. P.1 - Prob. 46ECh. P.1 - Prob. 47ECh. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - Prob. 50ECh. P.1 - Prob. 51ECh. P.1 - Prob. 52ECh. P.1 - Prob. 53ECh. P.1 - Prob. 54ECh. P.1 - Prob. 55ECh. P.1 - Prob. 56ECh. P.1 - Prob. 57ECh. P.1 - Prob. 58ECh. P.1 - Prob. 59ECh. P.1 - Prob. 60ECh. P.1 - Prob. 61ECh. P.1 - Prob. 62ECh. P.1 - Prob. 63ECh. P.1 - In Exercises 63 and 64, use scientific notation to...Ch. P.1 - Prob. 65ECh. P.1 - Prob. 66ECh. P.1 - Prob. 67ECh. P.1 - Prob. 68ECh. P.1 - Prob. 69ECh. P.1 - Prob. 70ECh. P.1 - Prob. 71ECh. P.1 - Prob. 72ECh. P.1 - Prob. 73ECh. P.1 - Prob. 74ECh. P.1 - Prob. 75ECh. P.1 - Prob. 76ECh. P.2 - Prob. 1QRCh. P.2 - Prob. 2QRCh. P.2 - Prob. 3QRCh. P.2 - Prob. 4QRCh. P.2 - Prob. 5QRCh. P.2 - Prob. 6QRCh. P.2 - Prob. 7QRCh. P.2 - Prob. 8QRCh. P.2 - Prob. 9QRCh. P.2 - Prob. 10QRCh. P.2 - Prob. 1ECh. P.2 - Prob. 2ECh. P.2 - Prob. 3ECh. P.2 - Prob. 4ECh. P.2 - Prob. 5ECh. P.2 - Prob. 6ECh. P.2 - Prob. 7ECh. P.2 - Prob. 8ECh. P.2 - Prob. 9ECh. P.2 - Prob. 10ECh. P.2 - Prob. 11ECh. P.2 - Prob. 12ECh. P.2 - Prob. 13ECh. P.2 - Prob. 14ECh. P.2 - Prob. 15ECh. P.2 - Prob. 16ECh. P.2 - Prob. 17ECh. P.2 - Prob. 18ECh. P.2 - Prob. 19ECh. P.2 - Prob. 20ECh. P.2 - Prob. 21ECh. P.2 - Prob. 22ECh. P.2 - Prob. 23ECh. P.2 - Prob. 24ECh. P.2 - Prob. 25ECh. P.2 - Prob. 26ECh. P.2 - Prob. 27ECh. P.2 - Prob. 28ECh. P.2 - Prob. 29ECh. P.2 - Prob. 30ECh. P.2 - Prob. 31ECh. P.2 - Prob. 32ECh. P.2 - Prob. 33ECh. P.2 - Prob. 34ECh. P.2 - Prob. 35ECh. P.2 - Prob. 36ECh. P.2 - Prob. 37ECh. P.2 - Prob. 38ECh. P.2 - Prob. 39ECh. P.2 - Prob. 40ECh. P.2 - Prob. 41ECh. P.2 - Prob. 42ECh. P.2 - Prob. 43ECh. P.2 - Prob. 44ECh. P.2 - Prob. 45ECh. P.2 - Prob. 46ECh. P.2 - Prob. 47ECh. P.2 - Prob. 48ECh. P.2 - Prob. 49ECh. P.2 - Prob. 50ECh. P.2 - Prob. 51ECh. P.2 - Prob. 52ECh. P.2 - Prob. 53ECh. P.2 - Prob. 54ECh. P.2 - Prob. 55ECh. P.2 - Prob. 56ECh. P.2 - Prob. 57ECh. P.2 - Prob. 58ECh. P.2 - Prob. 59ECh. P.2 - Prob. 60ECh. P.2 - Prob. 61ECh. P.2 - Prob. 62ECh. P.2 - Prob. 63ECh. P.2 - Prob. 64ECh. P.2 - Prob. 65ECh. P.2 - Prob. 66ECh. P.2 - Prob. 67ECh. P.2 - Prob. 68ECh. P.2 - Prob. 69ECh. P.2 - Prob. 70ECh. P.3 - Prob. 1QRCh. P.3 - Prob. 2QRCh. P.3 - Prob. 3QRCh. P.3 - Prob. 4QRCh. P.3 - Prob. 5QRCh. P.3 - Prob. 6QRCh. P.3 - Prob. 7QRCh. P.3 - Prob. 8QRCh. P.3 - Prob. 9QRCh. P.3 - Prob. 10QRCh. P.3 - Prob. 1ECh. P.3 - Prob. 2ECh. P.3 - Prob. 3ECh. P.3 - Prob. 4ECh. P.3 - Prob. 5ECh. P.3 - Prob. 6ECh. P.3 - Prob. 7ECh. P.3 - Prob. 8ECh. P.3 - Prob. 9ECh. P.3 - Prob. 10ECh. P.3 - Prob. 11ECh. P.3 - Prob. 12ECh. P.3 - Prob. 13ECh. P.3 - Prob. 14ECh. P.3 - Prob. 15ECh. P.3 - Prob. 16ECh. P.3 - Prob. 17ECh. P.3 - Prob. 18ECh. P.3 - Prob. 19ECh. P.3 - Prob. 20ECh. P.3 - Prob. 21ECh. P.3 - Prob. 22ECh. P.3 - Prob. 23ECh. P.3 - Prob. 24ECh. P.3 - Prob. 25ECh. P.3 - Prob. 26ECh. P.3 - Prob. 27ECh. P.3 - Prob. 28ECh. P.3 - Prob. 29ECh. P.3 - Prob. 30ECh. P.3 - Prob. 31ECh. P.3 - Prob. 32ECh. P.3 - Prob. 33ECh. P.3 - Prob. 34ECh. P.3 - Prob. 35ECh. P.3 - Prob. 36ECh. P.3 - Prob. 37ECh. P.3 - Prob. 38ECh. P.3 - Prob. 39ECh. P.3 - Prob. 40ECh. P.3 - Prob. 41ECh. P.3 - Prob. 42ECh. P.3 - Prob. 43ECh. P.3 - Prob. 44ECh. P.3 - Prob. 45ECh. P.3 - Prob. 46ECh. P.3 - Prob. 47ECh. P.3 - Prob. 48ECh. P.3 - Prob. 49ECh. P.3 - Prob. 50ECh. P.3 - Prob. 51ECh. P.3 - Prob. 52ECh. P.3 - Prob. 53ECh. P.3 - Prob. 54ECh. P.3 - Prob. 55ECh. P.3 - Prob. 56ECh. P.3 - Prob. 57ECh. P.3 - Prob. 58ECh. P.3 - Prob. 59ECh. P.3 - Prob. 60ECh. P.3 - Prob. 61ECh. P.3 - Prob. 62ECh. P.3 - Prob. 63ECh. P.3 - Prob. 64ECh. P.3 - Prob. 65ECh. P.3 - Prob. 66ECh. P.3 - Prob. 67ECh. P.3 - Prob. 68ECh. P.3 - Prob. 69ECh. P.3 - Prob. 70ECh. P.3 - Prob. 71ECh. P.3 - Prob. 72ECh. P.3 - Prob. 73ECh. P.4 - Prob. 1QRCh. P.4 - Prob. 2QRCh. P.4 - Prob. 3QRCh. P.4 - Prob. 4QRCh. P.4 - Prob. 5QRCh. P.4 - Prob. 6QRCh. P.4 - Prob. 7QRCh. P.4 - Prob. 8QRCh. P.4 - Prob. 9QRCh. P.4 - Prob. 10QRCh. P.4 - Prob. 1ECh. P.4 - Prob. 2ECh. P.4 - Prob. 3ECh. P.4 - Prob. 4ECh. P.4 - Prob. 5ECh. P.4 - Prob. 6ECh. P.4 - Prob. 7ECh. P.4 - Prob. 8ECh. P.4 - Prob. 9ECh. P.4 - Prob. 10ECh. P.4 - Prob. 11ECh. P.4 - Prob. 12ECh. P.4 - Prob. 13ECh. P.4 - Prob. 14ECh. P.4 - Prob. 15ECh. P.4 - Prob. 16ECh. P.4 - Prob. 17ECh. P.4 - Prob. 18ECh. P.4 - Prob. 19ECh. P.4 - Prob. 20ECh. P.4 - Prob. 21ECh. P.4 - Prob. 22ECh. P.4 - Prob. 23ECh. P.4 - Prob. 24ECh. P.4 - Prob. 25ECh. P.4 - Prob. 26ECh. P.4 - Prob. 27ECh. P.4 - Prob. 28ECh. P.4 - Prob. 29ECh. P.4 - Prob. 30ECh. P.4 - Prob. 31ECh. P.4 - Prob. 32ECh. P.4 - Prob. 33ECh. P.4 - Prob. 34ECh. P.4 - Prob. 35ECh. P.4 - Prob. 36ECh. P.4 - Prob. 37ECh. P.4 - Prob. 38ECh. P.4 - Prob. 39ECh. P.4 - Prob. 40ECh. P.4 - Prob. 41ECh. P.4 - Prob. 42ECh. P.4 - Prob. 43ECh. P.4 - Prob. 44ECh. P.4 - Prob. 45ECh. P.4 - Prob. 46ECh. P.4 - Prob. 47ECh. P.4 - Prob. 48ECh. P.4 - Prob. 49ECh. P.4 - Prob. 50ECh. P.4 - Prob. 51ECh. P.4 - Prob. 52ECh. P.4 - Prob. 53ECh. P.4 - Prob. 54ECh. P.4 - Prob. 55ECh. P.4 - Prob. 56ECh. P.4 - Prob. 57ECh. P.4 - Prob. 58ECh. P.4 - Prob. 59ECh. P.4 - Prob. 60ECh. P.4 - Prob. 61ECh. P.4 - Prob. 62ECh. P.4 - Prob. 63ECh. P.4 - Prob. 64ECh. P.4 - Prob. 65ECh. P.4 - Prob. 66ECh. P.4 - Prob. 67ECh. P.4 - Prob. 68ECh. P.4 - Prob. 69ECh. P.4 - Prob. 70ECh. P.4 - Prob. 71ECh. P.5 - Prob. 1QRCh. P.5 - Prob. 2QRCh. P.5 - Prob. 3QRCh. P.5 - Prob. 4QRCh. P.5 - Prob. 5QRCh. P.5 - Prob. 6QRCh. P.5 - Prob. 7QRCh. P.5 - Prob. 8QRCh. P.5 - Prob. 9QRCh. P.5 - Prob. 10QRCh. P.5 - Prob. 1ECh. P.5 - Prob. 2ECh. P.5 - Prob. 3ECh. P.5 - Prob. 4ECh. P.5 - Prob. 5ECh. P.5 - Prob. 6ECh. P.5 - Prob. 7ECh. P.5 - Prob. 8ECh. P.5 - Prob. 9ECh. P.5 - Prob. 10ECh. P.5 - Prob. 11ECh. P.5 - Prob. 12ECh. P.5 - Prob. 13ECh. P.5 - Prob. 14ECh. P.5 - Prob. 15ECh. P.5 - Prob. 16ECh. P.5 - Prob. 17ECh. P.5 - Prob. 18ECh. P.5 - Prob. 19ECh. P.5 - Prob. 20ECh. P.5 - Prob. 21ECh. P.5 - Prob. 22ECh. P.5 - Prob. 23ECh. P.5 - Prob. 24ECh. P.5 - Prob. 25ECh. P.5 - Prob. 26ECh. P.5 - Prob. 27ECh. P.5 - Prob. 28ECh. P.5 - Prob. 29ECh. P.5 - Prob. 30ECh. P.5 - Prob. 31ECh. P.5 - Prob. 32ECh. P.5 - Prob. 33ECh. P.5 - Prob. 34ECh. P.5 - Prob. 35ECh. P.5 - Prob. 36ECh. P.5 - Prob. 37ECh. P.5 - Prob. 38ECh. P.5 - Prob. 39ECh. P.5 - Prob. 40ECh. P.5 - Prob. 41ECh. P.5 - Prob. 42ECh. P.5 - Prob. 43ECh. P.5 - Prob. 44ECh. P.5 - Prob. 45ECh. P.5 - Prob. 46ECh. P.5 - Prob. 47ECh. P.5 - Prob. 48ECh. P.5 - Prob. 49ECh. P.5 - Prob. 50ECh. P.5 - Prob. 51ECh. P.5 - Prob. 52ECh. P.5 - Prob. 53ECh. P.5 - Prob. 54ECh. P.5 - Prob. 55ECh. P.5 - Prob. 56ECh. P.5 - Prob. 57ECh. P.5 - Prob. 58ECh. P.5 - Prob. 59ECh. P.5 - Prob. 60ECh. P.5 - Prob. 61ECh. P.5 - Prob. 62ECh. P.5 - Prob. 63ECh. P.5 - Prob. 64ECh. P.5 - Prob. 65ECh. P.5 - Prob. 66ECh. P.5 - Prob. 67ECh. P.5 - Prob. 68ECh. P.5 - Prob. 69ECh. P.5 - Prob. 70ECh. P.5 - Prob. 71ECh. P.6 - Prob. 1QRCh. P.6 - Prob. 2QRCh. P.6 - Prob. 3QRCh. P.6 - Prob. 4QRCh. P.6 - Prob. 5QRCh. P.6 - Prob. 6QRCh. P.6 - Prob. 7QRCh. P.6 - Prob. 8QRCh. P.6 - Prob. 9QRCh. P.6 - Prob. 10QRCh. P.6 - Prob. 1ECh. P.6 - Prob. 2ECh. P.6 - Prob. 3ECh. P.6 - Prob. 4ECh. P.6 - Prob. 5ECh. P.6 - Prob. 6ECh. P.6 - Prob. 7ECh. P.6 - Prob. 8ECh. P.6 - Prob. 9ECh. P.6 - Prob. 10ECh. P.6 - Prob. 11ECh. P.6 - Prob. 12ECh. P.6 - Prob. 13ECh. P.6 - Prob. 14ECh. P.6 - Prob. 15ECh. P.6 - Prob. 16ECh. P.6 - Prob. 17ECh. P.6 - Prob. 18ECh. P.6 - Prob. 19ECh. P.6 - Prob. 20ECh. P.6 - Prob. 21ECh. P.6 - Prob. 22ECh. P.6 - Prob. 23ECh. P.6 - Prob. 24ECh. P.6 - Prob. 25ECh. P.6 - Prob. 26ECh. P.6 - Prob. 27ECh. P.6 - Prob. 28ECh. P.6 - Prob. 29ECh. P.6 - Prob. 30ECh. P.6 - Prob. 31ECh. P.6 - Prob. 32ECh. P.6 - Prob. 33ECh. P.6 - Prob. 34ECh. P.6 - Prob. 35ECh. P.6 - Prob. 36ECh. P.6 - Prob. 37ECh. P.6 - Prob. 38ECh. P.6 - Prob. 39ECh. P.6 - Prob. 40ECh. P.6 - Prob. 41ECh. P.6 - Prob. 42ECh. P.6 - Prob. 43ECh. P.6 - Prob. 44ECh. P.6 - Prob. 45ECh. P.6 - Prob. 46ECh. P.6 - Prob. 47ECh. P.6 - Prob. 48ECh. P.6 - Prob. 49ECh. P.6 - Prob. 50ECh. P.6 - Prob. 51ECh. P.6 - Prob. 52ECh. P.6 - Prob. 53ECh. P.6 - Prob. 54ECh. P.6 - Prob. 55ECh. P.6 - Prob. 56ECh. P.6 - Prob. 57ECh. P.7 - Prob. 1QRCh. P.7 - Prob. 2QRCh. P.7 - Prob. 3QRCh. P.7 - Prob. 4QRCh. P.7 - Prob. 5QRCh. P.7 - Prob. 6QRCh. P.7 - Prob. 7QRCh. P.7 - Prob. 8QRCh. P.7 - Prob. 9QRCh. P.7 - Prob. 10QRCh. P.7 - Prob. 1ECh. P.7 - Prob. 2ECh. P.7 - Prob. 3ECh. P.7 - Prob. 4ECh. P.7 - Prob. 5ECh. P.7 - Prob. 6ECh. P.7 - Prob. 7ECh. P.7 - Prob. 8ECh. P.7 - Prob. 9ECh. P.7 - Prob. 10ECh. P.7 - Prob. 11ECh. P.7 - Prob. 12ECh. P.7 - Prob. 13ECh. P.7 - Prob. 14ECh. P.7 - Prob. 15ECh. P.7 - Prob. 16ECh. P.7 - Prob. 17ECh. P.7 - Prob. 18ECh. P.7 - Prob. 19ECh. P.7 - Prob. 20ECh. P.7 - Prob. 21ECh. P.7 - Prob. 22ECh. P.7 - Prob. 23ECh. P.7 - Prob. 24ECh. P.7 - Prob. 25ECh. P.7 - Prob. 26ECh. P.7 - Prob. 27ECh. P.7 - Prob. 28ECh. P.7 - Prob. 29ECh. P.7 - Prob. 30ECh. P.7 - Prob. 31ECh. P.7 - Prob. 32ECh. P.7 - Prob. 33ECh. P.7 - Prob. 34ECh. P.7 - Prob. 35ECh. P.7 - Prob. 36ECh. P.7 - Prob. 37ECh. P.7 - Prob. 38ECh. P.7 - Prob. 39ECh. P.7 - Prob. 40ECh. P.7 - Prob. 41ECh. P.7 - Prob. 42ECh. P.7 - Prob. 43ECh. P.7 - Prob. 44ECh. P.7 - Prob. 45ECh. P.7 - Prob. 46ECh. P.7 - Prob. 47ECh. P.7 - Prob. 48ECh. P - Prob. 1RECh. P - Prob. 2RECh. P - Prob. 3RECh. P - Prob. 4RECh. P - In Exercises 5 and 6, simplify the expression....Ch. P - Prob. 6RECh. P - Prob. 7RECh. P - Prob. 8RECh. P - Prob. 9RECh. P - Prob. 10RECh. P - Prob. 11RECh. P - Prob. 12RECh. P - Prob. 13RECh. P - Prob. 14RECh. P - Prob. 15RECh. P - Prob. 16RECh. P - Prob. 17RECh. P - Prob. 18RECh. P - Prob. 19RECh. P - Prob. 20RECh. P - Prob. 21RECh. P - Prob. 22RECh. P - Prob. 23RECh. P - Prob. 24RECh. P - Prob. 25RECh. P - Prob. 26RECh. P - Prob. 27RECh. P - Prob. 28RECh. P - Prob. 29RECh. P - Prob. 30RECh. P - Prob. 31RECh. P - Prob. 32RECh. P - Prob. 33RECh. P - Prob. 34RECh. P - Prob. 35RECh. P - Prob. 36RECh. P - Prob. 37RECh. P - Prob. 38RECh. P - Prob. 39RECh. P - Prob. 40RECh. P - Prob. 41RECh. P - Prob. 42RECh. P - Prob. 43RECh. P - Prob. 44RECh. P - Prob. 45RECh. P - Prob. 46RECh. P - Prob. 47RECh. P - Prob. 48RECh. P - Prob. 49RECh. P - Prob. 50RECh. P - Prob. 51RECh. P - Prob. 52RECh. P - Prob. 53RECh. P - Prob. 54RECh. P - Prob. 55RECh. P - Prob. 56RECh. P - Prob. 57RECh. P - Prob. 58RECh. P - Prob. 59RECh. P - Prob. 60RECh. P - Prob. 61RECh. P - Prob. 62RECh. P - Prob. 63RECh. P - Prob. 64RECh. P - Prob. 65RECh. P - Prob. 66RECh. P - Prob. 67RECh. P - Prob. 68RECh. P - Prob. 69RECh. P - Prob. 70RECh. P - Prob. 71RECh. P - Prob. 72RECh. P - Prob. 73RECh. P - Prob. 74RECh. P - Prob. 75RECh. P - Prob. 76RECh. P - Prob. 77RECh. P - Prob. 78RECh. P - Prob. 79RECh. P - Prob. 80RECh. P - Prob. 81RECh. P - Prob. 82RECh. P - Prob. 83RE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY