
A small-order coffee company charges $12 for each bag of coffee plus $3 shipping no matter how many bags are ordered. Describe a function that this situation gives rise to. Make a table for this function, sketch a graph of this function, and fund an equation for this function. Is the function linear or not? How can you tell?
To find: The function, make table for the function, sketch a graph of the function, also find the equation of function and also check whether the function is linear or not.
Answer to Problem 1P
The equation of the function is
Explanation of Solution
Given information:
The cost of each bag of coffee plus is $12 and $3 shipping charges no matter how many bags are order.
Calculation:
The above problem gives rise to a coffee bag function.
The input of the function is the number of bags of coffee ordered and output of the function is charges charged by the coffee company.
Consider
The table represent the given coffee bag function as shown in Table 1
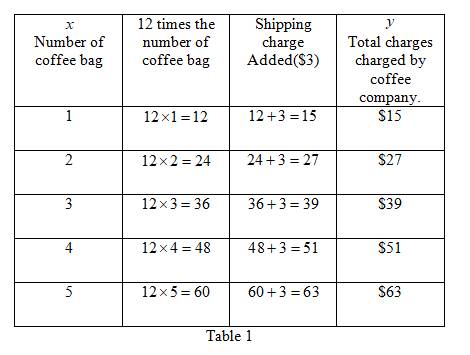
The number of coffee bags ordered is represented on
The point obtained from the Table 1 marked on the coordinate and join them.
The graph represented the given coffee bag function is shown in Figure 1.
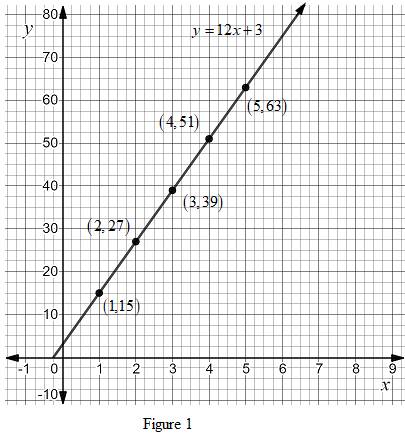
It is observed from the Figure 1 that the total charges charge by the company is the sum of cost of each coffee bag
Therefore, the equation of the given coffee bag function can be obtained as,
The above equation is linear function because the graph of linear function is a line.
Therefore, the equation of the function
Conclusion:
Thus, the equation of the function is
Want to see more full solutions like this?
Chapter 9 Solutions
Mathematics for Elementary Teachers with Activities (5th Edition)
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Thinking Mathematically (6th Edition)
Pre-Algebra Student Edition
Basic Business Statistics, Student Value Edition
- 8. Perform Singular Value Decomposition (SVD) on a Matrix The SVD problem can be found on page 66. Decompose the given matrix into its singular values, left singular vectors, and right singular vectors. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2ql5dbpVLCS/view? usp=sharing] Show the complete process and verify the decomposition.arrow_forward6. Diagonalize the Matrix and Verify the Result Check page 64 of the document for the matrix diagonalization problem. Find the eigenvalues and eigenvectors to diagonalize the matrix, then verify the result. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Present all calculations systematically.arrow_forward9. Analyze the Fourier Transform of a Discontinuous Function Refer to page 67 for the Fourier transform problem. Compute the Fourier transform of the given piecewise function and discuss its properties. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Present all steps in detail.arrow_forward
- 4. Determine the Taylor Series Expansion About a Point Refer to page 62 for the Taylor series problem. Find the Taylor series expansion of the function about the specified point and include the radius of convergence. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Explain the methodology and verify the series.arrow_forward10. Prove the Orthogonality of Eigenfunctions Go to page 68 of the document for the eigenfunction problem. Prove the orthogonality of the eigenfunctions of a given Sturm-Liouville problem. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide a rigorous proof, including necessary integrals and conditions.arrow_forwardShow what to do on the graph visually please!arrow_forward
- 1. Perform a Change of Variables for the Given Integral Refer to page 59 in the shared document for the integral problem. Apply a specified change of variables to simplify the integral and evaluate it. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Clearly outline each step in the transformation and solution.arrow_forward9. Solve the System of Ordinary Differential Equations Using Matrix Methods Turn to page 57 for the system of ODES. Solve the system using matrix methods, such as eigenvalue decomposition or diagonalization. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxp RyejKEMg1t2q15dbpVLCS/view? usp=sharing] Show a clear, step-by-step solution.arrow_forwardA study was done using a treatment group and a placebo group. The results are shown in the table. Assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Complete parts (a) and (b) below. Use a 0.05 significance level for both parts. a. Test the claim that the two samples are from populations with the same mean. What are the null and alternative hypotheses? OA. Ho PP2 H₁: P1 P2 OC. Ho H₁₂ H₁: P₁arrow_forward3. Solve the Differential Equation Using the Method of Characteristics Go to page 51 for a partial differential equation problem. Use the method of characteristics to solve the given equation. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxp RyejKEMg1t2ql5dbpVLCS/view? usp=sharing] Include all detailed steps in your solution.arrow_forward8. Determine the Fourier Series Expansion of the Function Refer to page 56 of the document for the Fourier series problem. Compute the Fourier series expansion of the given periodic function. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxp RyejKEMg1t2q15dbpVLCS/view? usp=sharing] Include all steps involved in the calculation.arrow_forwardFind the regression equation, letting the first variable be the predictor (x) variable. Using the listed lemon/crash data, where lemon imports are in metric tons and the fatality rates are per 100,000 people, find the best predicted crash fatality rate for a year in which there are 475 metric tons of lemon imports. Is the prediction worthwhile? Use a significance level of 0.05. Lemon Imports 235 264 356 Crash Fatality Rate 16 15.9 15.6 476 518 15.3 D 15.1 Find the equation of the regression line. + (Round the y-intercept to three decimal places as needed. Round the slope to four decimal places as needed.) The best predicted crash fatality rate for a year in which there are 475 metric tons of lemon imports is fatalities per 100,000 population. (Round to one decimal place as needed.) Is the prediction worthwhile? OA. Since there appears to be an outlier, the prediction is not appropriate. OB. Since all of the requirements for finding the equation of the regression line are met, the…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
 Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





