
Concept explainers
9.180 through 9.184 For the component described in the problem indicated, determine (a) the principal mass moments of inertia at the origin, (b) the principal axes of inertia at the origin. Sketch the body and show the orientation of the principal axes of inertia relative to the x, y, and z axes.
*9.183 Prob. 9.168
(a)
Find the principal mass moment of inertia of the cylinder at the origin O.
Answer to Problem 9.183P
The principal moment of inertia are
Explanation of Solution
Given information:
Refer Problem 9.168.
Show the moment of inertia as follows:
Calculation:
Show the Equation 9.56 as follows:
Substitute
Consider the value of
Solve the above Equation and get the value of
The principal moment of inertia are
Thus, The principal moment of inertia are
(b)
Find the angles made by the principal axis of inertia at O with the coordinate axis.
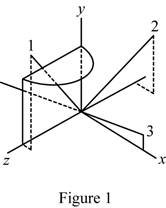
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis.
Answer to Problem 9.183P
The angles made by the principal axis of inertia at O with the coordinate axis is,
Explanation of Solution
Given information:
Consider the direction cosines of each principal axis are denoted by
Calculation:
Refer Part (a).
Consider K1.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (2).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
Consider K2.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (4).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
Consider K3.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (6).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
The angles made by the principal axis of inertia at O with the coordinate axis is,
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis as shown in Figure 1.
Want to see more full solutions like this?
Chapter 9 Solutions
EBK VECTOR MECHANICS FOR ENGINEERS: STA
- This is an exam review question. The answer is Pmin = 622.9 lb but whyarrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardThis is an old practice exam. Fce = 110lb and FBCD = 62 lb but whyarrow_forwardQuiz/An eccentrically loaded bracket is welded to the support as shown in Figure below. The load is static. The weld size for weld w1 is h1 = 4mm, for w2 h2 = 6mm, and for w3 is h3 =6.5 mm. Determine the safety factor (S.f) for the welds. F=29 kN. Use an AWS Electrode type (E100xx). 163 mm S 133 mm 140 mm Please solve the question above I solved the question but I'm sure the answer is wrong the link : https://drive.google.com/file/d/1w5UD2EPDiaKSx3W33aj Rv0olChuXtrQx/view?usp=sharingarrow_forward
- Q2: (15 Marks) A water-LiBr vapor absorption system incorporates a heat exchanger as shown in the figure. The temperatures of the evaporator, the absorber, the condenser, and the generator are 10°C, 25°C, 40°C, and 100°C respectively. The strong liquid leaving the pump is heated to 50°C in the heat exchanger. The refrigerant flow rate through the condenser is 0.12 kg/s. Calculate (i) the heat rejected in the absorber, and (ii) the COP of the cycle. Yo 8 XE-V lo 9 Pc 7 condenser 5 Qgen PG 100 Qabs Pe evaporator PRV 6 PA 10 3 generator heat exchanger 2 pump 185 absorberarrow_forwardQ5:(? Design the duct system of the figure below by using the balanced pressure method. The velocity in the duct attached to the AHU must not exceed 5m/s. The pressure loss for each diffuser is equal to 10Pa. 100CFM 100CFM 100CFM ☑ ☑ 40m AHU -16m- 8m- -12m- 57m 250CFM 40m -14m- 26m 36m ☑ 250CFMarrow_forwardA mass of ideal gas in a closed piston-cylinder system expands from 427 °C and 16 bar following the process law, pv1.36 = Constant (p times v to the power of 1.36 equals to a constant). For the gas, initial : final pressure ratio is 4:1 and the initial gas volume is 0.14 m³. The specific heat of the gas at constant pressure, Cp = 0.987 kJ/kg-K and the specific gas constant, R = 0.267 kJ/kg.K. Determine the change in total internal energy in the gas during the expansion. Enter your numerical answer in the answer box below in KILO JOULES (not in Joules) but do not enter the units. (There is no expected number of decimal points or significant figures).arrow_forward
- my ID# 016948724. Please solve this problem step by steparrow_forwardMy ID# 016948724 please find the forces for Fx=0: fy=0: fz=0: please help me to solve this problem step by steparrow_forwardMy ID# 016948724 please solve the proble step by step find the forces fx=o: fy=0; fz=0; and find shear moment and the bending moment diagran please draw the diagram for the shear and bending momentarrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
