Chapter 9.6, Problem 9.179P

(a)

To determine

Find the principal moment of inertia at the origin O.

Answer to Problem 9.179P

The principal moment of inertia at the origin O is $\underset{\_}{K_1=0.363m{a}^2,K_2=1.583m{a}^2,\text{and }{K}_3=1.72m{a}^2}$.

Explanation of Solution

Given information:

The mass of the cylinder is denoted by m.

The length of the circular cylinder is denoted by a.

The diameter OB of the top surface makes $45°$ with x and z axis.

Calculation:

Show the homogeneous circular cylinder as shown in Figure 1.

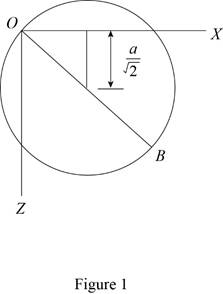
Refer Figure 1.

Refer Figure 9.28.

Apply parallel axis theorem

Show the moment of inertia of the circular cylinder about the y axis as follows:

$\begin{array}{c}{I}_y=\frac{1}{2}m{a}^2+m{a}^2\\ =\frac{3}{2}m{a}^2\end{array}$

Show the moment of inertia of the circular cylinder about the x and z axis as follows:

$I_x=I_z=\frac{1}{12}m\left(3a^2+L^2\right)+m\left[{\left(\frac{a}{\sqrt{2}}\right)}^2+{\left(\frac{a}{2}\right)}^2\right]\}$ (1)

Here, a is the radius of the cylinder and L is the length of the cylinder.

Substitute $a$ for L in Equation (1).

$\begin{array}{c}{I}_x=I_z=\frac{1}{12}m\left(3a^2+a^2\right)+m\left[{\left(\frac{a}{\sqrt{2}}\right)}^2+{\left(\frac{a}{2}\right)}^2\right]\\ =\frac{1}{3}m{a}^2+m\left[\frac{a^2}{2}+\frac{a^2}{4}\right]\\ =\frac{1}{3}m{a}^2+\frac{3}{4}m{a}^2\\ =\frac{13}{12}m{a}^2\end{array}$

The centroidal axis products of inertia are zero due to symmetry.

$I_{x^{\prime }{y}^{\prime }}=I_{y^{\prime }{z}^{\prime }}=I_{z^{\prime }{x}^{\prime }}=0$

Write the centroidal locations as measured from the origin O along the x, y and z axis as below;

$\overline{x}=\left(\frac{a}{\sqrt{2}}\right)$, $\overline{y}=\left(-\frac{a}{2}\right)$ and $\overline{z}=\left(\frac{a}{\sqrt{2}}\right)$.

Express the moment of inertia $I_{xy}$ as follows:

$\begin{array}{c}{I}_{xy}=I_{x^{\prime }{y}^{\prime }}+m\overline{x}\overline{y}\\ =0+m\left(\frac{a}{\sqrt{2}}\right)\left(-\frac{a}{2}\right)\\ =-\frac{1}{2\sqrt{2}}m{a}^2\end{array}$

Express the moment of inertia $I_{yz}$ as follows:

$\begin{array}{c}{I}_{yz}=I_{y^{\prime }{z}^{\prime }}+m\overline{y}\overline{z}\\ =0+m\left(-\frac{a}{2}\right)\left(\frac{a}{\sqrt{2}}\right)\\ =-\frac{1}{2\sqrt{2}}m{a}^2\end{array}$

Express the moment of inertia $I_{zx}$ as follows:

$\begin{array}{c}{I}_{zx}=I_{z^{\prime }{x}^{\prime }}+m\overline{z}\overline{x}\\ =0+m\left(\frac{a}{\sqrt{2}}\right)\left(\frac{a}{\sqrt{2}}\right)\\ =\frac{1}{2}m{a}^2\end{array}$

Show the Equation 9.56 as follows:

$\left\{\begin{array}{l}{K}^3-\left(I_x+I_y+I_z\right)K^2+\\ \left(I_x{I}_y+I_y{I}_z+I_z{I}_x-I_{xy}^2-I_{yz}^2-I_{zx}^2\right)K\\ -\left(I_x{I}_y{I}_z-I_x{I}_{yz}^2-I_y{I}_{zx}^2-I_z{I}_{xy}^2-2I_{xy}{I}_{yz}{I}_{zx}\right)\end{array}\right\}=0$

Substitute $\frac{13}{12}m{a}^2$ for $I_x$, $\frac{3}{2}m{a}^2$ for $I_y$, $\frac{13}{12}m{a}^2$ for $I_z$, $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{xy}$, $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{yz}$, and $\frac{1}{2}m{a}^2$ for $I_{zx}$.

$\begin{array}{l}\left\{\begin{array}{l}{K}^3-\left(\frac{13}{12}m{a}^2+\frac{3}{2}m{a}^2+\frac{13}{12}m{a}^2\right)K^2+\\ \left[\begin{array}{l}\left(\frac{13}{12}m{a}^2\right)\left(\frac{3}{2}m{a}^2\right)+\left(\frac{3}{2}m{a}^2\right)\left(\frac{13}{12}m{a}^2\right)+\left(\frac{13}{12}m{a}^2\right)\left(\frac{13}{12}m{a}^2\right)\\ -{\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)}^2-{\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)}^2-{\left(\frac{1}{2}m{a}^2\right)}^2\end{array}\right]K\\ -\left[\begin{array}{l}\left(\frac{13}{12}m{a}^2\right)\left(\frac{3}{2}m{a}^2\right)\left(\frac{13}{12}m{a}^2\right)-\left(\frac{13}{12}m{a}^2\right){\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)}^2\\ -\left(\frac{3}{2}m{a}^2\right){\left(\frac{1}{2}m{a}^2\right)}^2-\left(\frac{13}{12}m{a}^2\right){\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)}^2\\ -2\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)\left(-\frac{1}{2\sqrt{2}}m{a}^2\right)\left(\frac{1}{2}m{a}^2\right)\end{array}\right]\end{array}\right\}=0\\ \left\{\begin{array}{l}{K}^3-\left(\frac{13}{12}+\frac{3}{2}+\frac{13}{12}\right)K^{2}m{a}^2+\\ \left[\begin{array}{l}\left(\frac{13}{12}\right)\left(\frac{3}{2}\right)+\left(\frac{3}{2}\right)\left(\frac{13}{12}\right)+\left(\frac{13}{12}\right)\left(\frac{13}{12}\right)\\ -{\left(-\frac{1}{2\sqrt{2}}\right)}^2-{\left(-\frac{1}{2\sqrt{2}}\right)}^2-{\left(\frac{1}{2}\right)}^2\end{array}\right]K{\left(m{a}^2\right)}^2\\ -\left[\begin{array}{l}\left(\frac{3}{2}\right)\left(\frac{13}{12}\right)\left(\frac{13}{12}\right)-\left(\frac{13}{12}\right){\left(-\frac{1}{2\sqrt{2}}\right)}^2\\ -\left(\frac{3}{2}\right){\left(\frac{1}{2}\right)}^2-\left(\frac{13}{12}\right){\left(-\frac{1}{2\sqrt{2}}\right)}^2\\ -2\left(-\frac{1}{2\sqrt{2}}\right)\left(-\frac{1}{2\sqrt{2}}\right)\left(\frac{1}{2}\right)\end{array}\right]{\left(m{a}^2\right)}^3\end{array}\right\}=0\end{array}$

Substitute $m{a}^2\zeta$ for $K$.

${\zeta }^3-\frac{11}{3}{\zeta }^2+\frac{565}{144}\zeta -\frac{95}{96}=0$

Solve the above Equation and get the values of ${\zeta }_1$, ${\zeta }_2$, and ${\zeta }_3$ as follows:

$\begin{array}{l}{\zeta }_1=0.363\\ {\zeta }_2=1.583\\ {\zeta }_3=1.72\end{array}$

Show the principal moment of inertia as follows:

$\begin{array}{l}{K}_1=0.363m{a}^2\\ K_2=1.583m{a}^2\\ K_3=1.72m{a}^2\end{array}$

Thus, the principal mass moment of inertia are $\underset{\_}{K_1=0.363m{a}^2,K_2=1.583m{a}^2,\text{and }{K}_3=1.72m{a}^2}$

(b)

To determine

Find the angles made by the principal axis of inertia at O with the coordinate axis.

Answer to Problem 9.179P

The angles made by the principal axis of inertia at O with the coordinate axis is $\underset{\_}{{\left({\theta }_x\right)}_1=49.7°,{\left({\theta }_y\right)}_1=113.7°,{\left({\theta }_z\right)}_1=49.7°},\underset{\_}{{\left({\theta }_x\right)}_2=45°,{\left({\theta }_y\right)}_2=90°,{\left({\theta }_z\right)}_2=135°},\underset{\_}{{\left({\theta }_x\right)}_3=73.5°,{\left({\theta }_y\right)}_3=23.7°,{\left({\theta }_z\right)}_3=73.5°}$.

Explanation of Solution

Given information:

Consider the direction cosines of each principal axis are denoted by ${\lambda }_x,{\lambda }_y,{\lambda }_z$.

Calculation:

Refer Part (a).

Show the Equation 9.54 as follows:

$\begin{array}{l}\left(I_x-K\right){\lambda }_x-I_{xy}{\lambda }_y-I_{zx}{\lambda }_z=0\\ -I_{zx}{\lambda }_x-I_{yz}{\lambda }_y+\left(I_z-K\right){\lambda }_z=0\end{array}\}$ (2)

Substitute $\frac{13}{12}m{a}^2$ for $I_x$, $\frac{13}{12}m{a}^2$ for $I_z$, $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{xy}$, $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{yz}$, and $\frac{1}{2}m{a}^2$ for $I_{zx}$.

$\begin{array}{l}\left(\frac{13}{12}m{a}^2-K\right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right)m{a}^2{\lambda }_y-\left(\frac{1}{2}m{a}^2\right){\lambda }_z=0\\ -\left(\frac{1}{2}m{a}^2\right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right)m{a}^2{\lambda }_y+\left(\frac{13}{12}m{a}^2-K\right){\lambda }_z=0\end{array}\}$ (3)

Modify Equation (3).

Consider $K=m{a}^2\zeta$. Then,

$\begin{array}{l}\left(\frac{13}{12}-\zeta \right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right){\lambda }_y-\left(\frac{1}{2}\right){\lambda }_z=0\\ -\left(\frac{1}{2}\right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right){\lambda }_y+\left(\frac{13}{12}-\zeta \right){\lambda }_z=0\end{array}\}$ (4)

Solve Equation (4).

$\begin{array}{l}\frac{13}{12}-\zeta =-\frac{1}{2}\\ \zeta =\frac{19}{12}\end{array}$

Add both the Equation in Equation (4).

$\begin{array}{l}\left[\frac{13}{12}-\zeta -\left(-\frac{1}{2}\right)\right]{\lambda }_x+\left[-\frac{1}{2}-\left(\frac{13}{12}-\zeta \right)\right]{\lambda }_z=0\\ {\lambda }_x={\lambda }_z\end{array}$

Substitute ${\lambda }_x$ for ${\lambda }_z$ in Equation (4).

$\begin{array}{l}\left(\frac{13}{12}-\zeta \right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right){\lambda }_y-\left(\frac{1}{2}\right){\lambda }_x=0\\ -\left(-\frac{1}{2\sqrt{2}}\right){\lambda }_y=\left(\frac{1}{2}-\frac{13}{12}+\zeta \right){\lambda }_x\\ \left(\frac{1}{2\sqrt{2}}\right){\lambda }_y=\left(\zeta -\frac{7}{12}\right){\lambda }_x\\ {\lambda }_y=2\sqrt{2}\left(\zeta -\frac{7}{12}\right){\lambda }_x\end{array}$

Show the Equation 9.57 as follows:

${\lambda }_x^2+{\lambda }_y^2+{\lambda }_z^2=1$

Substitute $2\sqrt{2}\left(\zeta -\frac{7}{12}\right){\lambda }_x$ for ${\lambda }_y$, and ${\lambda }_x$ for ${\lambda }_z$.

$\begin{array}{l}{\lambda }_x^2+{\left[2\sqrt{2}\left(\zeta -\frac{7}{12}\right){\lambda }_x\right]}^2+{\lambda }_x^2=1\\ {\lambda }_x^2+8{\left(\zeta -\frac{7}{12}\right)}^2{\lambda }_x^2+{\lambda }_x^2=1\\ \left[2+8{\left(\zeta -\frac{7}{12}\right)}^2\right]{\lambda }_x^2=1\end{array}$ (5)

Consider K1.

Substitute $0.363$ for ${\zeta }_1$ in Equation (5).

$\begin{array}{l}\left[2+8{\left(0.363-\frac{7}{12}\right)}^2\right]{\left({\lambda }_x\right)}_1^2=1\\ {\left({\lambda }_x\right)}_1={\left({\lambda }_z\right)}_1=0.647249\end{array}$

Calculate the value of ${\left({\lambda }_y\right)}_1$ as follows:

$\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_1=\left({\zeta }_1-\frac{7}{12}\right){\left({\lambda }_x\right)}_1$

Substitute $0.647249$ for ${\left({\lambda }_x\right)}_1$ and $0.363$ for ${\zeta }_1$.

$\begin{array}{l}\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_1=\left(0.363-\frac{7}{12}\right)\times 0.647249\\ {\left({\lambda }_y\right)}_1=-0.402662\end{array}$

Show the direction cosines ${\left({\theta }_x\right)}_1,{\left({\theta }_y\right)}_1,{\left({\theta }_z\right)}_1$ using the relation:

$\begin{array}{c}\cos {\left({\theta }_x\right)}_1={\left({\lambda }_x\right)}_1=0.647249\\ {\left({\theta }_x\right)}_1={\cos }^{-1}\left(0.647249\right)\\ =49.7°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_z\right)}_1={\left({\lambda }_z\right)}_1=0.647249\\ {\left({\theta }_z\right)}_1={\cos }^{-1}\left(0.647249\right)\\ =49.7°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_y\right)}_1={\left({\lambda }_y\right)}_1=-0.402662\\ {\left({\theta }_y\right)}_1={\cos }^{-1}\left(-0.402662\right)\\ =113.7°\end{array}$

Conisder K3.

Substitute $1.720$ for ${\zeta }_3$ in Equation (5).

$\begin{array}{l}\left[2+8{\left(1.720-\frac{7}{12}\right)}^2\right]{\left({\lambda }_x\right)}_3^2=1\\ {\left({\lambda }_x\right)}_3={\left({\lambda }_z\right)}_3=0.284726\end{array}$

Calculate the value of ${\left({\lambda }_y\right)}_3$ as follows:

$\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_3=\left({\zeta }_3-\frac{7}{12}\right){\left({\lambda }_x\right)}_3$

Substitute $0.284726$ for ${\left({\lambda }_x\right)}_3$ and $1.720$ for ${\zeta }_3$.

$\begin{array}{l}\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_3=\left(1.720-\frac{7}{12}\right)\times 0.647249\\ {\left({\lambda }_y\right)}_3=0.915348\end{array}$

Show the direction cosines ${\left({\theta }_x\right)}_3,{\left({\theta }_y\right)}_3,{\left({\theta }_z\right)}_3$ using the relation:

$\begin{array}{c}\cos {\left({\theta }_x\right)}_3={\left({\lambda }_x\right)}_3=0.284726\\ {\left({\theta }_x\right)}_3={\cos }^{-1}\left(0.284726\right)\\ =73.5°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_z\right)}_3={\left({\lambda }_z\right)}_3=0.284726\\ {\left({\theta }_z\right)}_3={\cos }^{-1}\left(0.284726\right)\\ =73.5°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_y\right)}_3={\left({\lambda }_y\right)}_3=0.915348\\ {\left({\theta }_y\right)}_3={\cos }^{-1}\left(0.915348\right)\\ =23.7°\end{array}$

Consider K2.

Show the Equation 9.54b as follows:

$-I_{xy}{\lambda }_x+\left(I_y-K\right){\lambda }_y-I_{yz}{\lambda }_z=0$

Substitute $\frac{3}{2}m{a}^2$ for $I_y$, $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{xy}$, and $-\frac{1}{2\sqrt{2}}m{a}^2$ for $I_{yz}$.

$\begin{array}{l}-\left(-\frac{1}{2\sqrt{2}}m{a}^2\right){\lambda }_x+\left(\frac{3}{2}m{a}^2-K\right){\lambda }_y+\left(\frac{1}{2\sqrt{2}}m{a}^2\right){\lambda }_z=0\\ \frac{1}{2\sqrt{2}}{\lambda }_x+\left(\frac{3}{2}-\zeta \right){\lambda }_y+\left(\frac{1}{2\sqrt{2}}\right){\lambda }_z=0\end{array}$ (6)

Refer Equation (3) and (6).

$\begin{array}{l}\left(\frac{13}{12}-\zeta \right){\lambda }_x-\left(-\frac{1}{2\sqrt{2}}\right){\lambda }_y-\left(\frac{1}{2}\right){\lambda }_z=0\\ \frac{1}{2\sqrt{2}}{\lambda }_x+\left(\frac{3}{2}-\zeta \right){\lambda }_y+\left(\frac{1}{2\sqrt{2}}\right){\lambda }_z=0\end{array}\}$ (7)

Substitute $\frac{19}{12}$ for $\zeta$ in Equation (4).

$\begin{array}{l}\left(\frac{13}{12}-\frac{19}{12}\right){\left({\lambda }_x\right)}_2-\left(-\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_2-\left(\frac{1}{2}\right){\left({\lambda }_z\right)}_2=0\\ \frac{1}{2\sqrt{2}}{\left({\lambda }_x\right)}_2+\left(\frac{3}{2}-\frac{19}{12}\right){\left({\lambda }_y\right)}_2+\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_z\right)}_2=0\end{array}$

Modify above Equations as follows:

$\begin{array}{l}\frac{1}{12}{\left({\lambda }_x\right)}_2+\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_y\right)}_2-\left(\frac{1}{2}\right){\left({\lambda }_z\right)}_2=0\\ \frac{1}{2\sqrt{2}}{\left({\lambda }_x\right)}_2-\frac{1}{12}{\left({\lambda }_y\right)}_2+\left(\frac{1}{2\sqrt{2}}\right){\left({\lambda }_z\right)}_2=0\end{array}\}$ (8)

Solve Equation (8) and get the value of ${\left({\lambda }_y\right)}_2=0$.

Show the Equation 9.57 as follows:

$\begin{array}{l}{\left({\lambda }_x\right)}_2^2+{\left({\lambda }_y\right)}_2^2+{\left({\lambda }_z\right)}_2^2=1\\ {\left({\lambda }_x\right)}_2^2+0+{\left({\lambda }_z\right)}_2^2=1\\ {\left({\lambda }_x\right)}_2^2+{\left({\lambda }_z\right)}_2^2=1\end{array}$

Substitute ${\lambda }_x$ for ${\lambda }_z$.

$\begin{array}{l}{\left({\lambda }_x\right)}_2^2+{\left({\lambda }_x\right)}_2^2=1\\ {\left({\lambda }_x\right)}_2=\frac{1}{\sqrt{2}}\end{array}$

${\left({\lambda }_z\right)}_2=-\frac{1}{\sqrt{2}}$

Show the direction cosines ${\left({\theta }_x\right)}_2,{\left({\theta }_y\right)}_2,{\left({\theta }_z\right)}_2$ using the relation:

$\begin{array}{c}\cos {\left({\theta }_x\right)}_2={\left({\lambda }_x\right)}_2=\frac{1}{\sqrt{2}}\\ {\left({\theta }_x\right)}_2={\cos }^{-1}\left(\frac{1}{\sqrt{2}}\right)\\ =45°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_z\right)}_2={\left({\lambda }_z\right)}_2=-\left(\frac{1}{\sqrt{2}}\right)\\ {\left({\theta }_z\right)}_2={\cos }^{-1}\left(-\frac{1}{\sqrt{2}}\right)\\ =135°\end{array}$

$\begin{array}{c}\cos {\left({\theta }_y\right)}_2={\left({\lambda }_y\right)}_2=0\\ {\left({\theta }_y\right)}_2={\cos }^{-1}\left(0\right)\\ =90°\end{array}$

Thus, the velocity of the point B is $\underset{\_}{1.537\text{ft/s}\left(\text{Acting }77.48°\text{Clockwise above the horizontal}\right)}$.

(c)

To determine

Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis.

Explanation of Solution

Given information:

Calculation:

Refer Part (a) and (b).

Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis as shown in Figure 2.

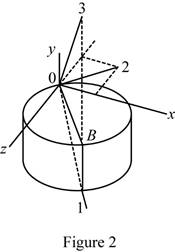
Refer Figure 2.

The principal axis 1 and 3 lies on the vertical plane of symmetry passing through OB.

The principal axis 2 lies in xz plane.