Chapter 9.6, Problem 13WE

To determine

To calculate: To identify the conic, find its center and foci (in any) and draw the graph

Answer to Problem 13WE

Conic is hyperbola and center is $\left(1,-3\right)$ , coordinates of foci are $\left(1+\sqrt{5},-3\right)$ and $\left(1-\sqrt{5},-3\right)$

Explanation of Solution

Given information: Equation of conic is $x^2-4y^2-2x-24y-39=0$

Formula Used:

The hyperbola with center $\left(h,k\right)$ and foci $\left(-c,0\right)$ and $\left(c,0\right)$ and difference of focal radii $2a$ has the equation:

  $\frac{{\left(x-h\right)}^2}{a^2}-\frac{{\left(y-k\right)}^2}{b^2}=1$ , where $b^2=c^2-a^2$

Equation of the asymptotes are $y=\pm \frac{b}{a}\left(x-h\right)+k$

The hyperbola with center $\left(h,k\right)$ and foci $\left(0,-c\right)$ and $\left(0,c\right)$ and difference of focal radii $2a$ has the equation:

  $\frac{{\left(y-k\right)}^2}{a^2}-\frac{{\left(x-h\right)}^2}{b^2}=1$ , where $b^2=c^2-a^2$

Equation of the asymptotes are $y=\pm \frac{a}{b}\left(x-h\right)+k$

Calculation:

Equation of conic is given as follows:

  $x^2-4y^2-2x-24y-39=0$

Rewriting and divide both sides of equation by $36$

  $\begin{array}{l}\left(x^2-2x+1\right)-\left(4y^2+24y+36\right)+36-1-39=0\\ \left(x^2-2x+1\right)-4\left(y^2+6y+9\right)=4\\ {\left(x-1\right)}^2-4{\left(y+3\right)}^2=4\\ \frac{{\left(x-1\right)}^2}{4}-\frac{{\left(y+3\right)}^2}{1}=1\\ \frac{{\left(x-1\right)}^2}{2^2}-\frac{{\left(y+3\right)}^2}{1^2}=1\end{array}$

Above conic is a hyperbola

Comparing the equation with standard form of the equation of hyperbola $\frac{{\left(x-h\right)}^2}{a^2}-\frac{{\left(y-k\right)}^2}{b^2}=1$ :

  $\begin{array}{l}a=2\\ b=1\end{array}$

Centre is $\left(1,-3\right)$

Foci is calculated as follows:

  $\begin{array}{l}{b}^2=c^2-a^2\\ c^2=a^2+b^2\\ c^2=2^2+1^2\\ c^2=4+1\\ c^2=5\\ c=\pm \sqrt{5}\end{array}$

Thus, Foci are $\left(1+\sqrt{5},-3\right)$ and $\left(1-\sqrt{5},-3\right)$

Graph the hyperbola as follows:

  

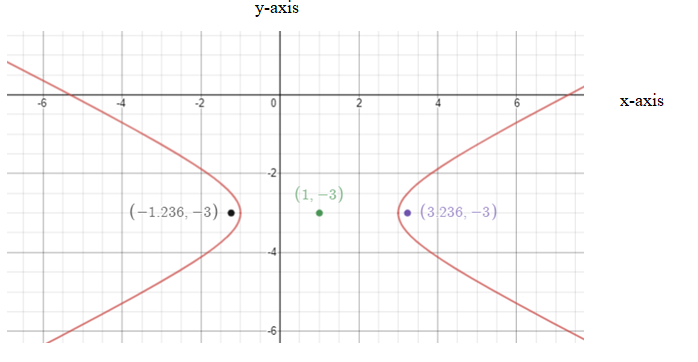
Conclusion:

Hence, conic is hyperbola and center is $\left(1,-3\right)$ , coordinates of foci are $\left(1+\sqrt{5},-3\right)$ and $\left(1-\sqrt{5},-3\right)$