Mathematical Methods in the Physical Sciences
3rd Edition
ISBN: 9780471198260
Author: Mary L. Boas
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9.5, Problem 22P
For the following problems, use the Lagrangian to find the equations of motion and then refer to Chapter 3, Section 12.
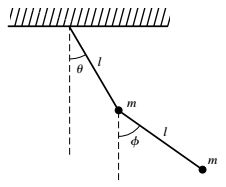
Do Problem 21 if the two masses are different. Let
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
12:25 AM Sun Dec 22
uestion 6- Week 8: QuX
Assume that a company X +
→ C
ezto.mheducation.com
Week 8: Quiz i
Saved
6
4
points
Help
Save & Exit
Submit
Assume that a company is considering purchasing a machine for $50,000 that will have a five-year useful life and a $5,000 salvage value. The
machine will lower operating costs by $17,000 per year. The company's required rate of return is 15%. The net present value of this investment
is closest to:
Click here to view Exhibit 12B-1 and Exhibit 12B-2, to determine the appropriate discount factor(s) using the tables provided.
00:33:45
Multiple Choice
О
$6,984.
$11,859.
$22,919.
○ $9,469,
Mc
Graw
Hill
2
100-
No chatgpt pls will upvote
7. [10 marks]
Let G
=
(V,E) be a 3-connected graph. We prove that for every x, y, z Є V, there is a
cycle in G on which x, y, and z all lie.
(a) First prove that there are two internally disjoint xy-paths Po and P₁.
(b) If z is on either Po or P₁, then combining Po and P₁ produces a cycle on which
x, y, and z all lie. So assume that z is not on Po and not on P₁. Now prove that
there are three paths Qo, Q1, and Q2 such that:
⚫each Qi starts at z;
• each Qi ends at a vertex w; that is on Po or on P₁, where wo, w₁, and w₂ are
distinct;
the paths Qo, Q1, Q2 are disjoint from each other (except at the start vertex
2) and are disjoint from the paths Po and P₁ (except at the end vertices wo,
W1, and w₂).
(c) Use paths Po, P₁, Qo, Q1, and Q2 to prove that there is a cycle on which x, y, and
z all lie. (To do this, notice that two of the w; must be on the same Pj.)
Chapter 9 Solutions
Mathematical Methods in the Physical Sciences
Ch. 9.1 - The speed of light in a medium of index of...Ch. 9.1 - The speed of light in a medium of index of...Ch. 9.1 - The speed of light in a medium of index of...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...
Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.2 - Write and solve the Euler equations to make the...Ch. 9.3 - Change the independent variable to simplify the...Ch. 9.3 - Change the independent variable to simplify the...Ch. 9.3 - Change the independent variable to simplify the...Ch. 9.3 - Change the independent variable to simplify the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Write and solve the Euler equations to make the...Ch. 9.3 - Use Fermats principle to find the path followed by...Ch. 9.3 - Use Fermats principle to find the path followed by...Ch. 9.3 - Use Fermats principle to find the path followed by...Ch. 9.3 - Use Fermats principle to find the path followed by...Ch. 9.3 - Find the geodesics on a plane using polar...Ch. 9.3 - Prob. 16PCh. 9.3 - Find the geodesics on the cone x2+y2=z2. Hint: Use...Ch. 9.3 - Find the geodesics on a sphere. Hints: Use...Ch. 9.4 - Verify equations (4.2).Ch. 9.4 - Show, in Figure 4.4, that for a point like...Ch. 9.4 - In the brachistochrone problem, show that if the...Ch. 9.4 - Consider a rapid transit system consisting of...Ch. 9.4 - In Problems 5 to 7, use Fermats principle to find...Ch. 9.4 - In Problems 5 to 7, use Fermats principle to find...Ch. 9.4 - In Problems 5 to 7, use Fermats principle to find...Ch. 9.5 - (a) Consider the case of two dependent variables....Ch. 9.5 - Set up Lagranges equations in cylindrical...Ch. 9.5 - Do Problem 2 in spherical coordinates.Ch. 9.5 - Use Lagranges equations to find the equation of...Ch. 9.5 - Find the equation of motion of a particle moving...Ch. 9.5 - A particle moves on the surface of a sphere of...Ch. 9.5 - Prove that a particle constrained to stay on a...Ch. 9.5 - Two particles each of mass m are connected by an...Ch. 9.5 - A mass m moves without friction on the surface of...Ch. 9.5 - Do Example 3 above, using cylindrical coordinates...Ch. 9.5 - A yo-yo (as shown) falls under gravity. Assume...Ch. 9.5 - Find the Lagrangian and Lagranges equations for a...Ch. 9.5 - A particle moves without friction under gravity on...Ch. 9.5 - 2A hoop of mass M and radius a rolls without...Ch. 9.5 - Generalize Problem 14 to any mass M of circular...Ch. 9.5 - Find the Lagrangian and the Lagrange equation for...Ch. 9.5 - A simple pendulum (Problem 4) is suspended from a...Ch. 9.5 - A hoop of mass m in a vertical plane rests on a...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.5 - For the following problems, use the Lagrangian to...Ch. 9.6 - In Problems 1 and 2, given the length l of a curve...Ch. 9.6 - In Problems 1 and 2, given the length l of a curve...Ch. 9.6 - Given 10 cc of lead, find how to form it into a...Ch. 9.6 - Prob. 4PCh. 9.6 - A curve y=y(x), joining two points x1 and x2 on...Ch. 9.6 - In Problem 5, given the volume, find the shape of...Ch. 9.6 - Integrate (6.2), simplify the result and integrate...Ch. 9.8 - (a) In Section 3, we showed how to obtain a first...Ch. 9.8 - Find a first integral of the Euler equation to...Ch. 9.8 - Find a first integral of the Euler equation to...Ch. 9.8 - Find a first integral of the Euler equation to...Ch. 9.8 - Write and solve the Euler equations to make...Ch. 9.8 - Write and solve the Euler equations to make...Ch. 9.8 - Write and solve the Euler equations to make...Ch. 9.8 - Find the geodesics on the cylinder r=1+cos.Ch. 9.8 - Prob. 9MPCh. 9.8 - Find the geodesics on the parabolic cylinder y=x2.Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - In Problems 11 to 18, use Fermats principle to...Ch. 9.8 - Find Lagranges equations in polar coordinates for...Ch. 9.8 - Repeat Problem 19 if V=K/r.Ch. 9.8 - Write Lagranges equations in cylindrical...Ch. 9.8 - In spherical coordinates, find the Lagrange...Ch. 9.8 - A particle slides without friction around a...Ch. 9.8 - Write and simplify the Euler equation to make...Ch. 9.8 - Prob. 25MPCh. 9.8 - A wire carrying a uniform distribution of positive...Ch. 9.8 - Find a first integral of the Euler equation for...Ch. 9.8 - Write the Lagrange equation for a particle moving...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The 16 sequences in the sample space S.
Probability And Statistical Inference (10th Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Constructing and Graphing Discrete Probability Distributions In Exercises 19 and 20, (a) construct a probabilit...
Elementary Statistics: Picturing the World (7th Edition)
A person has 8 friends, of whom S will be invited to a party. a. How many choices are there if 2 of the friends...
A First Course in Probability (10th Edition)
In track, the second lane from the inside of the track is longer than the inside lane. Use this information to ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forward
- Q/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forwardRefer to page 100 for problems on graph theory and linear algebra. Instructions: • Analyze the adjacency matrix of a given graph to find its eigenvalues and eigenvectors. • Interpret the eigenvalues in the context of graph properties like connectivity or clustering. Discuss applications of spectral graph theory in network analysis. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 110 for problems on optimization. Instructions: Given a loss function, analyze its critical points to identify minima and maxima. • Discuss the role of gradient descent in finding the optimal solution. . Compare convex and non-convex functions and their implications for optimization. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 140 for problems on infinite sets. Instructions: • Compare the cardinalities of given sets and classify them as finite, countable, or uncountable. • Prove or disprove the equivalence of two sets using bijections. • Discuss the implications of Cantor's theorem on real-world computation. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 120 for problems on numerical computation. Instructions: • Analyze the sources of error in a given numerical method (e.g., round-off, truncation). • Compute the error bounds for approximating the solution of an equation. • Discuss strategies to minimize error in iterative methods like Newton-Raphson. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 145 for problems on constrained optimization. Instructions: • Solve an optimization problem with constraints using the method of Lagrange multipliers. • • Interpret the significance of the Lagrange multipliers in the given context. Discuss the applications of this method in machine learning or operations research. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Only 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward3. [10 marks] Let Go (Vo, Eo) and G₁ = (V1, E1) be two graphs that ⚫ have at least 2 vertices each, ⚫are disjoint (i.e., Von V₁ = 0), ⚫ and are both Eulerian. Consider connecting Go and G₁ by adding a set of new edges F, where each new edge has one end in Vo and the other end in V₁. (a) Is it possible to add a set of edges F of the form (x, y) with x € Vo and y = V₁ so that the resulting graph (VUV₁, Eo UE₁ UF) is Eulerian? (b) If so, what is the size of the smallest possible F? Prove that your answers are correct.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Differential Equation | MIT 18.01SC Single Variable Calculus, Fall 2010; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=HaOHUfymsuk;License: Standard YouTube License, CC-BY