Chapter 9.4, Problem 69PE

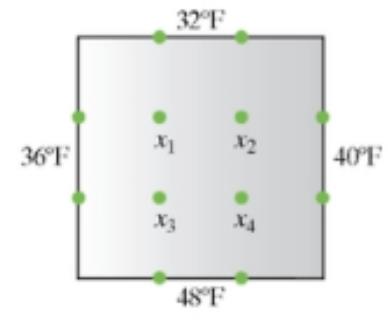
Physicists know that if each edge of a thin conducting plate is kept at a constant temperature, then the temperature at the interior points is the mean (average) of the four surrounding points equidistant from the interior point. Use this principle in Exercise 69 to find the temperature at points $x_1,x_2,x_3$ , and $x_4$ .

Hint: Set up four linear equations to represent the temperature at points $x_1,x_2,x_3$ , and $x_4$ . Then solve the system. For example, one equation would be:

$x_1=\frac{1}{4}\left(36+32+x_2+x_3\right)$