
Concept explainers
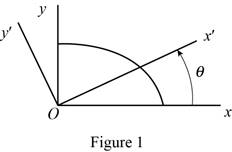
Determine for the quarter ellipse of Prob. 9.67 the moments of inertia and the product of inertia with respect to new axes obtained by rotating the x and y axes about O (a) through 45° counterclockwise, (b) through 30° clockwise.
9.67 through 9.70 Determine by direct integration the product of inertia of the given area with respect to the x and y axes.
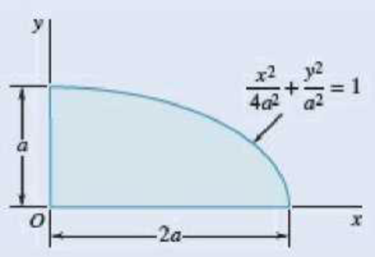
Fig. P9.67
(a)
Find the moment of inertia and product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y axes about O through
Answer to Problem 9.79P
The moment of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the x about O through
The moment of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the y about O through
The product of inertia for quarter ellipse with respect to new centroid axes obtained by rotating the x and y about O through
Explanation of Solution
Calculation:
Sketch the quarter ellipse as shown in Figure 1.
Refer to Figure 9.12 “Moments of inertia of common geometric Shapes” in the textbook.
Find the moment of inertia
Here, a is moments and products of area for a quarter of a circle of radius.
Substitute
Find the moment of inertia
Substitute
Refer to problem 9.67.
Write the curve Equation as shown below:
Modify Equation (3).
Select a vertical strip as differential element of area.
Applying the parallel axis theorem.
Here,
Using the property of symmetry about x and y axis.
Express the variables in terms of x and y.
Find the coordinate of centroid element
Substitute
Consider the element strip as follows:
Integrating
Find the value of
Find the value of
Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through
Refer to Equation 9.18 in section 9.3B in the textbook.
Substitute
Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through
Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through
Refer to Equation 9.19 in section 9.3B in the textbook.
Substitute
Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through
Find the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through
Substitute
Thus, the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through
(b)
Find the moment of inertia and product of inertia with respect new centroid axes obtained by rotating the x and y axes about O through
Answer to Problem 9.79P
The moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through
The moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through
The product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through
Explanation of Solution
Calculation:
Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through
Refer to Equation 9.18 in section 9.3B in the textbook.
Substitute
Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x about O through
Find the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through
Refer to Equation 9.19 in section 9.3B in the textbook.
Substitute
Thus, the moment of inertia for quarter ellipse with respect new centroid axes obtained by rotating the y about O through
Find the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through
Substitute
Thus, the product of inertia for quarter ellipse with respect new centroid axes obtained by rotating the x and y about O through
Want to see more full solutions like this?
Chapter 9 Solutions
VECTOR MECHANICS FOR ENGINEERS: STATICS
- Can you answer this question?arrow_forwardCan you answer this question?arrow_forwardA gear has a gear wheel with 16 teeth. The gear should be dimensioned for the highest and lowest gear ratio. Looking for output power, torque, speed?nin= 2000 rpmmin = 30Nmn=0,9a max= 450 mmModule 4Gear limitsz1 z213 13-1614 14-2615 15-4516 16-10117 17-131418 18-…..I have calculate but I can’t get the right answers…..√16 =459x60/56x57=1.1 lowest59x60/13x13=20,94 highestnut=2000/1.1= 1818rpmnut=2000/20.94=95.5 rpmMut=1.1x30=33 NmMut=20.94x30=628,2 Nm(Right answer)LowestZ=13, M=24,4Nm, n=2462 rpmHighestZ=92, M=172,5Nm, n=347,8 rpmP=5655W on botharrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





