Chapter 9.2, Problem 63AYU

In Problems 63-68, graph each pair of polar equations on the same polar grid. Find the polar coordinates of the point(s) of intersection and label the point(s) on the graph.

$r=\sin \theta ;r=1+\cos \theta$

To determine

To find: Graph the polar equations $r = \text{sin} \theta ; r = 1 + \text{cos} \theta$ on the same polar grid and find the point of intersections if any.

Answer to Problem 63AYU

Solution

The graph of the polar equations $r = \text{sin} \theta ; r = 1 + \text{cos} \theta$ are equation of an circle and equation of a cardioids.

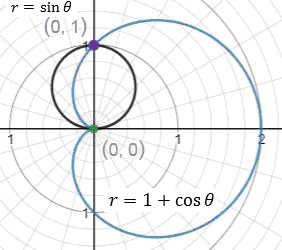
From the above graph, the point of intersections are $\left(0, 1\right) \text{and} \left(0, 0\right)$.

Given:

It is asked to graph the polar equations $r = \text{sin} \theta ; r = 1 + \text{cos} \theta$.

Explanation of Solution

Formula to be used:

$\left(r \text{cos} \theta , r \text{sin} \theta \right)=\left(x, y\right)$

Equation of circle passing through the pole, tangent to the polar axis, center on the line $\theta = \frac{\pi }{2}$, radius $a$ is given by the equation

$r = \pm 2a \text{sin} \theta , a > 0.$

Cardioids are characterized by equations of the form

$r = a\left(1 \pm \text{cos} \theta \right)$

$r = a\left(1 \pm \text{sin} \theta \right)$

where $a > 0$. The graph of a cardioid passes through the pole.

Consider $r = \text{sin} \theta$,

This polar equation can be written as

$r = 2\left(\frac{1}{2}\right) \text{sin} \theta$

The above equation is an equation of circle passing through the pole, tangent to the polar axis, center on the line $\theta = \frac{\pi }{2}$, radius $\frac{1}{2}$.

Consider $r = 1 + \text{cos} \theta$,

$r = 4 \csc \theta = 4\frac{1}{\text{sin} \theta }r \text{sin} \theta = 4$

Which is nothing but the horizontal line at $4$.

To sketch:

$r = \text{sin} \theta ; r = 1 + \text{cos} \theta$.

From the above graph, the point of intersections are (0,1) and (0,0).