
Mathematics All Around-Workbook
6th Edition
ISBN: 9780134462356
Author: Pirnot
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Chapter 9.2, Problem 11E
To determine
To find:
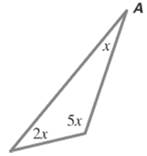
The measure of angle A of the below given triangle.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Need help with the following statistic problems.
om
nearest tenth if necessary.
milsum 3.
છે.
9.3mm
3mm
A
78-43-92
4-3) 11.7 of
72.04-11.7-=
lygons
7.8 mi
60.94
blants"
9 om
6.
4.15-7
16- 32m
1.8m
4.5m
%
ose
4.5m
as to
65m
14
represents 5 square meters.
Need help with the following questions on statistics.
Chapter 9 Solutions
Mathematics All Around-Workbook
Ch. 9.1 - In Exercise 18, match each term with the numbered...Ch. 9.1 - In Exercise 18, match each term with the numbered...Ch. 9.1 - In Exercise 18, match each term with the numbered...Ch. 9.1 - In Exercise 18, match each term with the numbered...Ch. 9.1 - Prob. 5ECh. 9.1 - Prob. 6ECh. 9.1 - Prob. 7ECh. 9.1 - In Exercise 18, match each term with the numbered...Ch. 9.1 - In Exercises 914, determine whether each statement...Ch. 9.1 - In Exercises 914, determine whether each statement...
Ch. 9.1 - In Exercises 914, determine whether each statement...Ch. 9.1 - In Exercises 914, determine whether each statement...Ch. 9.1 - In Exercises 914, determine whether each statement...Ch. 9.1 - In Exercises 914, determine whether each statement...Ch. 9.1 - Use the given figure to answer Exercises 1518....Ch. 9.1 - Use the given figure to answer Exercises 1518....Ch. 9.1 - Use the given figure to answer Exercises 1518....Ch. 9.1 - Use the given figure to answer Exercises 1518....Ch. 9.1 - Prob. 19ECh. 9.1 - Prob. 20ECh. 9.1 - In Exercises 1924, find the measure of a...Ch. 9.1 - In Exercises 1924, find the measure of a...Ch. 9.1 - In Exercises 1924, find the measure of a...Ch. 9.1 - In Exercises 1924, find the measure of a...Ch. 9.1 - Prob. 25ECh. 9.1 - Prob. 26ECh. 9.1 - In Exercises 2530, find the measures of angles a,...Ch. 9.1 - In Exercises 2530, find the measures of angles a,...Ch. 9.1 - In Exercises 2530, find the measures of angles a,...Ch. 9.1 - Prob. 30ECh. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - In Exercises 3136, you are given two of the...Ch. 9.1 - Prob. 37ECh. 9.1 - Continuing the situation from Exercises 3136, use...Ch. 9.1 - Continuing the situation from Exercises 3136, use...Ch. 9.1 - Continuing the situation from Exercises 3136, use...Ch. 9.1 - Prob. 41ECh. 9.1 - In Exercises 4144, solve for x. Assume that lines...Ch. 9.1 - In Exercises 4144, solve for x. Assume that lines...Ch. 9.1 - Prob. 44ECh. 9.1 - Prob. 45ECh. 9.1 - Prob. 46ECh. 9.1 - Prob. 47ECh. 9.1 - Prob. 48ECh. 9.1 - Prob. 49ECh. 9.1 - Prob. 50ECh. 9.1 - Prob. 51ECh. 9.1 - Prob. 52ECh. 9.1 - Prob. 53ECh. 9.1 - Prob. 54ECh. 9.1 - Prob. 55ECh. 9.1 - Prob. 56ECh. 9.1 - In Exercises 57 and 58 find the measure of angle x...Ch. 9.1 - Prob. 58ECh. 9.1 - Prob. 59ECh. 9.1 - Prob. 60ECh. 9.1 - Prob. 61ECh. 9.1 - When a pair of parallel lines is cut by a...Ch. 9.1 - Prob. 63ECh. 9.1 - Prob. 64ECh. 9.1 - Prob. 65ECh. 9.1 - Prob. 66ECh. 9.1 - Prob. 67ECh. 9.1 - Prob. 68ECh. 9.1 - Prob. 69ECh. 9.1 - Prob. 70ECh. 9.1 - Prob. 71ECh. 9.1 - Prob. 72ECh. 9.1 - Prob. 73ECh. 9.1 - Prob. 74ECh. 9.1 - Prob. 75ECh. 9.1 - Prob. 76ECh. 9.1 - Prob. 77ECh. 9.1 - Prob. 78ECh. 9.1 - Prob. 79ECh. 9.1 - Prob. 80ECh. 9.2 - In Exercises 14, state whether each figure is a...Ch. 9.2 - In Exercises 14, state whether each figure is a...Ch. 9.2 - Prob. 3ECh. 9.2 - In Exercises 14, state whether each figure is a...Ch. 9.2 - Prob. 5ECh. 9.2 - Provide a counterexample to each of the statements...Ch. 9.2 - Prob. 7ECh. 9.2 - Prob. 8ECh. 9.2 - Prob. 9ECh. 9.2 - Prob. 10ECh. 9.2 - Prob. 11ECh. 9.2 - We have indicated the measures of the angles of...Ch. 9.2 - Prob. 13ECh. 9.2 - We have indicated the measures of the angles of...Ch. 9.2 - Prob. 15ECh. 9.2 - If we divide a regular octagon into triangles as...Ch. 9.2 - What is the measure of an interior angle of a...Ch. 9.2 - What is the measure of an interior angle of a...Ch. 9.2 - Prob. 19ECh. 9.2 - Prob. 20ECh. 9.2 - Prob. 21ECh. 9.2 - Prob. 22ECh. 9.2 - Prob. 23ECh. 9.2 - Prob. 24ECh. 9.2 - Prob. 25ECh. 9.2 - Prob. 26ECh. 9.2 - Prob. 27ECh. 9.2 - An accessibility ramp. A ramp was constructed to...Ch. 9.2 - The Russians erected the worlds largest...Ch. 9.2 - Prob. 30ECh. 9.2 - Prob. 31ECh. 9.2 - Prob. 32ECh. 9.2 - Prob. 33ECh. 9.2 - Prob. 34ECh. 9.2 - Prob. 35ECh. 9.2 - Prob. 36ECh. 9.2 - Prob. 37ECh. 9.2 - Prob. 38ECh. 9.2 - Prob. 39ECh. 9.2 - Prob. 40ECh. 9.2 - The tangram is an ancient Chinese puzzle that...Ch. 9.2 - The tangram is an ancient Chinese puzzle that...Ch. 9.2 - The tangram is an ancient Chinese puzzle that...Ch. 9.2 - Prob. 44ECh. 9.2 - Prob. 45ECh. 9.2 - Prob. 46ECh. 9.2 - Prob. 47ECh. 9.2 - What information do you know about the angles and...Ch. 9.2 - Do an Internet search for architectural disasters...Ch. 9.2 - Prob. 51ECh. 9.2 - Prob. 52ECh. 9.2 - Prob. 53ECh. 9.2 - Prob. 54ECh. 9.2 - Prob. 55ECh. 9.2 - Make up a description of a triangle as we did in...Ch. 9.2 - Prob. 57ECh. 9.2 - Prob. 58ECh. 9.2 - Prob. 59ECh. 9.2 - Prob. 60ECh. 9.2 - Prob. 61ECh. 9.2 - Prob. 63ECh. 9.2 - In building scaffolding, often the scaffolding has...Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 112, find the area of each figure....Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - In Exercises 1318, find the area of the shaded...Ch. 9.3 - The area of trapezoid ABCD is 54 square feet and...Ch. 9.3 - The area of trapezoid ABCD is 80 square inches....Ch. 9.3 - Prob. 21ECh. 9.3 - Prob. 22ECh. 9.3 - Prob. 23ECh. 9.3 - Prob. 24ECh. 9.3 - Prob. 25ECh. 9.3 - Prob. 26ECh. 9.3 - Prob. 27ECh. 9.3 - In Exercises 2730, find the length of side x for...Ch. 9.3 - Prob. 29ECh. 9.3 - Prob. 30ECh. 9.3 - In Exercises 31 and 32, find the area of triangle...Ch. 9.3 - Prob. 32ECh. 9.3 - Prob. 33ECh. 9.3 - Prob. 34ECh. 9.3 - Prob. 35ECh. 9.3 - A geoboard is a board with rows of nails spaced 1...Ch. 9.3 - Prob. 37ECh. 9.3 - Prob. 38ECh. 9.3 - Prob. 39ECh. 9.3 - Prob. 40ECh. 9.3 - In Exercises 4144, state whether perimeter or area...Ch. 9.3 - Prob. 42ECh. 9.3 - Prob. 43ECh. 9.3 - Prob. 44ECh. 9.3 - Prob. 45ECh. 9.3 - Prob. 46ECh. 9.3 - Find the length of line segment AB in the given...Ch. 9.3 - Prob. 48ECh. 9.3 - Prob. 49ECh. 9.3 - Use the following figure to answer Exercises 49...Ch. 9.3 - Prob. 51ECh. 9.3 - Prob. 52ECh. 9.3 - Prob. 53ECh. 9.3 - Prob. 54ECh. 9.3 - Prob. 55ECh. 9.3 - Prob. 56ECh. 9.3 - Prob. 57ECh. 9.3 - Prob. 58ECh. 9.3 - Prob. 59ECh. 9.3 - Prob. 60ECh. 9.3 - Prob. 61ECh. 9.3 - Prob. 62ECh. 9.3 - Prob. 63ECh. 9.3 - Prob. 64ECh. 9.3 - Prob. 65ECh. 9.3 - Prob. 66ECh. 9.3 - Prob. 67ECh. 9.3 - Prob. 68ECh. 9.3 - Prob. 69ECh. 9.3 - Prob. 70ECh. 9.3 - Prob. 71ECh. 9.3 - Prob. 72ECh. 9.3 - Prob. 73ECh. 9.3 - Prob. 74ECh. 9.3 - Prob. 75ECh. 9.3 - Prob. 76ECh. 9.3 - Prob. 77ECh. 9.3 - Prob. 78ECh. 9.3 - Prob. 79ECh. 9.3 - Prob. 80ECh. 9.3 - Prob. 81ECh. 9.3 - Prob. 82ECh. 9.3 - Prob. 83ECh. 9.3 - Prob. 84ECh. 9.3 - Prob. 85ECh. 9.3 - Prob. 86ECh. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 18, find a the surface area and b the...Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - In Exercises 914, find the volume of each figure.Ch. 9.4 - Prob. 15ECh. 9.4 - Prob. 16ECh. 9.4 - Prob. 17ECh. 9.4 - Prob. 18ECh. 9.4 - Prob. 19ECh. 9.4 - Prob. 20ECh. 9.4 - Prob. 21ECh. 9.4 - Prob. 22ECh. 9.4 - Prob. 23ECh. 9.4 - Prob. 24ECh. 9.4 - Prob. 25ECh. 9.4 - Prob. 26ECh. 9.4 - Prob. 27ECh. 9.4 - Prob. 28ECh. 9.4 - Prob. 29ECh. 9.4 - Prob. 30ECh. 9.4 - Prob. 31ECh. 9.4 - Prob. 32ECh. 9.4 - Prob. 33ECh. 9.4 - Prob. 34ECh. 9.4 - Diameter of the moon. Earth has a diameter of...Ch. 9.4 - Prob. 36ECh. 9.4 - Prob. 37ECh. 9.4 - Prob. 38ECh. 9.4 - Prob. 39ECh. 9.4 - Prob. 40ECh. 9.4 - Prob. 41ECh. 9.4 - Prob. 42ECh. 9.4 - Prob. 43ECh. 9.4 - Prob. 44ECh. 9.4 - Prob. 45ECh. 9.4 - Prob. 46ECh. 9.4 - Prob. 47ECh. 9.4 - Prob. 48ECh. 9.4 - Prob. 49ECh. 9.4 - Prob. 50ECh. 9.4 - Prob. 51ECh. 9.4 - Prob. 52ECh. 9.4 - Prob. 53ECh. 9.4 - Prob. 54ECh. 9.4 - If we cut off the top of a cone by making a...Ch. 9.5 - Use Table 9.5 to make the conversions in Exercises...Ch. 9.5 - Use Table 9.5 to make the conversions in Exercises...Ch. 9.5 - Prob. 3ECh. 9.5 - Prob. 4ECh. 9.5 - Prob. 5ECh. 9.5 - Prob. 6ECh. 9.5 - Prob. 7ECh. 9.5 - Prob. 8ECh. 9.5 - Prob. 9ECh. 9.5 - Prob. 10ECh. 9.5 - Prob. 11ECh. 9.5 - Prob. 12ECh. 9.5 - Prob. 13ECh. 9.5 - Prob. 14ECh. 9.5 - Prob. 15ECh. 9.5 - Prob. 16ECh. 9.5 - Prob. 17ECh. 9.5 - Pick the most appropriate measurement for each of...Ch. 9.5 - Prob. 19ECh. 9.5 - Prob. 20ECh. 9.5 - Prob. 21ECh. 9.5 - Prob. 22ECh. 9.5 - Prob. 23ECh. 9.5 - Prob. 24ECh. 9.5 - Prob. 25ECh. 9.5 - Prob. 26ECh. 9.5 - Prob. 27ECh. 9.5 - Prob. 28ECh. 9.5 - Prob. 29ECh. 9.5 - Prob. 30ECh. 9.5 - Prob. 31ECh. 9.5 - Prob. 32ECh. 9.5 - Prob. 33ECh. 9.5 - Prob. 34ECh. 9.5 - Prob. 35ECh. 9.5 - Our monetary system is based on powers of 10 much...Ch. 9.5 - Prob. 37ECh. 9.5 - Prob. 38ECh. 9.5 - Prob. 39ECh. 9.5 - Prob. 40ECh. 9.5 - Prob. 41ECh. 9.5 - Rewrite each statement, replacing the metric...Ch. 9.5 - Prob. 43ECh. 9.5 - Prob. 44ECh. 9.5 - Area of an oriental rug. a. Find the number of...Ch. 9.5 - Prob. 46ECh. 9.5 - Prob. 47ECh. 9.5 - Prob. 48ECh. 9.5 - Prob. 49ECh. 9.5 - Prob. 50ECh. 9.5 - Prob. 51ECh. 9.5 - Prob. 52ECh. 9.5 - Prob. 53ECh. 9.5 - Prob. 54ECh. 9.5 - Prob. 55ECh. 9.5 - Prob. 56ECh. 9.5 - Buying gasoline. If gasoline costs 2.18 per liter...Ch. 9.5 - Prob. 58ECh. 9.5 - Prob. 59ECh. 9.5 - Prob. 60ECh. 9.5 - Prob. 61ECh. 9.5 - Prob. 62ECh. 9.5 - Prob. 63ECh. 9.5 - Prob. 64ECh. 9.5 - Prob. 65ECh. 9.5 - Prob. 66ECh. 9.5 - Prob. 67ECh. 9.5 - Prob. 68ECh. 9.5 - Prob. 69ECh. 9.5 - In the metric system, temperatures are measured on...Ch. 9.5 - Prob. 71ECh. 9.5 - Prob. 72ECh. 9.5 - Prob. 73ECh. 9.5 - Prob. 74ECh. 9.5 - Prob. 75ECh. 9.5 - Prob. 76ECh. 9.5 - Prob. 77ECh. 9.5 - Prob. 78ECh. 9.5 - Prob. 79ECh. 9.5 - Prob. 80ECh. 9.5 - Prob. 81ECh. 9.5 - Prob. 82ECh. 9.5 - Prob. 83ECh. 9.5 - Prob. 84ECh. 9.5 - Prob. 85ECh. 9.5 - Prob. 86ECh. 9.5 - Cost of gasoline in France. Suppose that you are...Ch. 9.5 - Prob. 88ECh. 9.5 - Prob. 89ECh. 9.5 - Prob. 90ECh. 9.6 - Use the following figure for Exercises 14. You may...Ch. 9.6 - Prob. 2ECh. 9.6 - Prob. 3ECh. 9.6 - Prob. 4ECh. 9.6 - Prob. 5ECh. 9.6 - Prob. 6ECh. 9.6 - Prob. 7ECh. 9.6 - Prob. 8ECh. 9.6 - Prob. 9ECh. 9.6 - Prob. 10ECh. 9.6 - Use the following figure for Exercises 1114....Ch. 9.6 - Prob. 12ECh. 9.6 - Prob. 13ECh. 9.6 - Prob. 14ECh. 9.6 - Perform the indicated glide reflection on figure...Ch. 9.6 - Perform the indicated glide reflection on figure...Ch. 9.6 - Prob. 17ECh. 9.6 - Prob. 18ECh. 9.6 - Prob. 19ECh. 9.6 - Prob. 20ECh. 9.6 - Prob. 21ECh. 9.6 - Prob. 22ECh. 9.6 - Prob. 23ECh. 9.6 - Prob. 24ECh. 9.6 - Prob. 25ECh. 9.6 - Prob. 26ECh. 9.6 - Prob. 27ECh. 9.6 - Prob. 28ECh. 9.6 - Prob. 29ECh. 9.6 - Prob. 30ECh. 9.6 - Prob. 31ECh. 9.6 - Prob. 32ECh. 9.6 - Prob. 33ECh. 9.6 - Prob. 34ECh. 9.6 - Prob. 35ECh. 9.6 - Prob. 36ECh. 9.6 - Prob. 37ECh. 9.6 - Prob. 38ECh. 9.6 - Prob. 39ECh. 9.6 - Prob. 40ECh. 9.6 - Prob. 41ECh. 9.6 - Prob. 42ECh. 9.6 - Prob. 43ECh. 9.6 - Prob. 44ECh. 9.6 - Prob. 45ECh. 9.6 - Prob. 46ECh. 9.6 - Prob. 47ECh. 9.6 - Prob. 48ECh. 9.6 - Prob. 49ECh. 9.6 - Prob. 50ECh. 9.6 - Prob. 51ECh. 9.6 - Which of the following types of tessellations can...Ch. 9.6 - Prob. 53ECh. 9.6 - Prob. 54ECh. 9.6 - Prob. 55ECh. 9.6 - Prob. 56ECh. 9.6 - Prob. 57ECh. 9.7 - Prob. 1ECh. 9.7 - Prob. 2ECh. 9.7 - Prob. 3ECh. 9.7 - Prob. 4ECh. 9.7 - Prob. 5ECh. 9.7 - Prob. 6ECh. 9.7 - Prob. 7ECh. 9.7 - Prob. 8ECh. 9.7 - Prob. 9ECh. 9.7 - Prob. 10ECh. 9.7 - Prob. 11ECh. 9.7 - Prob. 12ECh. 9.7 - Prob. 13ECh. 9.7 - Prob. 14ECh. 9.7 - Prob. 15ECh. 9.7 - Prob. 16ECh. 9.7 - How did we argue that the length of the Koch curve...Ch. 9.7 - Prob. 18ECh. 9.7 - Prob. 19ECh. 9.7 - Prob. 20ECh. 9.7 - Prob. 21ECh. 9.7 - Prob. 22ECh. 9.7 - Prob. 23ECh. 9.7 - Prob. 24ECh. 9.7 - Prob. 25ECh. 9.CR - Prob. 1CRCh. 9.CR - Prob. 2CRCh. 9.CR - Prob. 3CRCh. 9.CR - Prob. 4CRCh. 9.CR - Prob. 5CRCh. 9.CR - Prob. 6CRCh. 9.CR - Prob. 7CRCh. 9.CR - Prob. 8CRCh. 9.CR - Prob. 9CRCh. 9.CR - Prob. 10CRCh. 9.CR - Prob. 11CRCh. 9.CR - Prob. 12CRCh. 9.CR - Find the volume of each solid. a bCh. 9.CR - Prob. 14CRCh. 9.CR - Prob. 15CRCh. 9.CR - Prob. 16CRCh. 9.CR - Prob. 17CRCh. 9.CR - Prob. 18CRCh. 9.CR - Prob. 19CRCh. 9.CR - Prob. 20CRCh. 9.CR - Prob. 21CRCh. 9.CR - Prob. 22CRCh. 9.CR - Prob. 23CRCh. 9.CR - Prob. 24CRCh. 9.CR - Prob. 25CRCh. 9.CR - You are given steps 0 and 1 for constructing a...Ch. 9.CT - In the given figure, name each of the following...Ch. 9.CT - Prob. 2CTCh. 9.CT - Prob. 3CTCh. 9.CT - Prob. 4CTCh. 9.CT - Prob. 5CTCh. 9.CT - Prob. 6CTCh. 9.CT - Prob. 7CTCh. 9.CT - Prob. 8CTCh. 9.CT - Prob. 9CTCh. 9.CT - Prob. 10CTCh. 9.CT - Prob. 11CTCh. 9.CT - A pool is surrounded by a brick walkway as shown...Ch. 9.CT - Prob. 13CTCh. 9.CT - Prob. 14CTCh. 9.CT - Prob. 15CTCh. 9.CT - Prob. 16CTCh. 9.CT - Prob. 17CTCh. 9.CT - Prob. 18CTCh. 9.CT - Prob. 19CTCh. 9.CT - Prob. 20CTCh. 9.CT - Prob. 21CTCh. 9.CT - Prob. 22CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Need help with these following statistic questions.arrow_forwardNo chatgpt plsarrow_forwardAfter a great deal of experimentation, two college senior physics majors determined that when a bottle of French champagne is shaken several times, held upright, and uncorked, its cork travels according to the function below, where s is its height (in feet) above the ground t seconds after being released. s(t)=-16t² + 30t+3 a. How high will it go? b. How long is it in the air?arrow_forward
- 2PM Tue Mar 4 7 Dashboard Calendar To Do Notifications Inbox File Details a 25/SP-CIT-105-02 Statics for Technicians Q-7 Determine the resultant of the load system shown. Locate where the resultant intersects grade with respect to point A at the base of the structure. 40 N/m 2 m 1.5 m 50 N 100 N/m Fig.- Problem-7 4 m Gradearrow_forwardif δ ≥ 2, then it contains a cycle with length at least δ + 1.arrow_forward+6x²+135x+1) (0≤x≤10). a) Find the number of units The total profit P(x) (in thousands of dollars) from a sale of x thousand units of a new product is given by P(x) = In (-x²+6x² + 135x+ that should be sold in order to maximize the total profit. b) What is the maximum profit?arrow_forward
- 7. Find the doubling time of an investment earning 2.5% interest compounded a) semiannually b) continuouslyarrow_forward6. Find the time it will take $1000 to grow to $5000 at an interest rate of 3.5% if the interest is compounded a) quarterly b) continuouslyarrow_forwardA smallish urn contains 16 small plastic bunnies - 9 of which are pink and 7 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X=6)[Select] (b) P(X>7) ≈ [Select]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Maths - Geometry - What is an Angle - English; Author: Bodhaguru;https://www.youtube.com/watch?v=bsuDcCjFq6c;License: Standard YouTube License, CC-BY
What is an Angle? | Different Types of Angles | Geometry | Math | LetsTute; Author: Let'stute;https://www.youtube.com/watch?v=aGejx2fRCHU;License: Standard Youtube License