
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
14th Edition
ISBN: 9780133918922
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 9.1, Problem 1P
Locate the center of mass of the homogeneous rod bent into the shape of a circular arc.
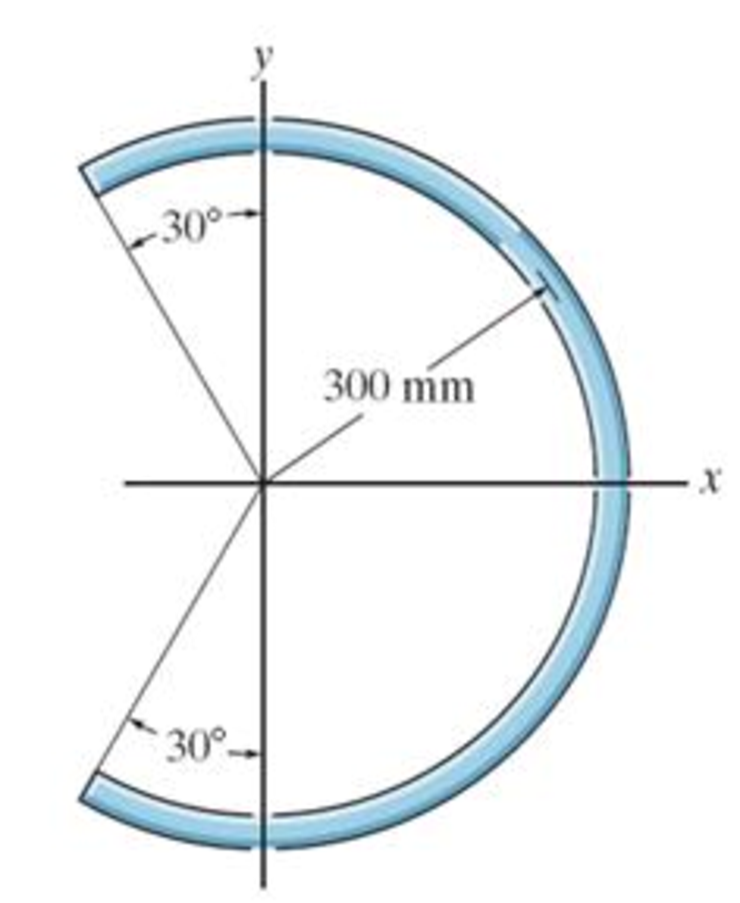
9-1.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
ә
レ
Figure below shows a link mechanism in which the link OA rotates uniformly in an
anticlockwise direction at 10 rad/s. the lengths of the various links are OA=75 mm, OB-150 mm,
BC=150 mm, CD-300 mm. Determine for the position shown, the sliding velocity of D.
A
A
B
#
Space Diagram
o NTS (Not-to-Scale)
C
10
=--20125
735)
750 x2.01
اه
2
レ
Tanism in which the link OA mm. O
anticlockwise direction at 10 rad/s, the lengths of the various links are OA=75mm, OB=150mm,
BC=150mm,CD=300mm. Determine for the position shown, the sliding velocity of D.
A
A
Space Diagram
o NT$ (Not-to-Scale)
B
#
C
か
750 x2.01
165
79622
Ashaft fitted with a flywheel rotates at 300 rpm. and drives a machine. The torque
required to drive the machine varies in a cyclic manner over a period of 2 revolutions. The torque drops
from 20,000 Nm to 10,000 Nm uniformly during 90 degrees and remains constant for the following 180
degrees. It then rises uniformly to 35,000 Nm during the next 225 degrees and after that it drops to
20,000 in a uniform manner for 225 degrees, the cycle being repeated thereafter.
Determine the power required to drive the machine and percentage fluctuation in speed, if the driving
torque applied to the shaft is constant and the mass of the flywheel is 12 tonnes with radius of gyration of
500 mm. What is the maximum angular acceleration of the flywheel.
35,000
TNM
20,000
10,000
0
90
270
495
Crank angle 8 degrees
720
Chapter 9 Solutions
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
Ch. 9.1 - In each case, use the element shown and specify...Ch. 9.1 - Determine the centroid (x,y) of the shaded area....Ch. 9.1 - Determine the centroid (x,y) of the shaded area....Ch. 9.1 - Determine the centroid of the shaded area. Prob....Ch. 9.1 - Locate the center of mass x of the straight rod if...Ch. 9.1 - Locate the centroid of the homogeneous solid...Ch. 9.1 - Locate the centroid z of the homogeneous solid...Ch. 9.1 - Locate the center of mass of the homogeneous rod...Ch. 9.1 - Determine the location (x,y) of the centroid of...Ch. 9.1 - If the rod has a weight per unit length of 100...
Ch. 9.1 - Locate the center of gravity of the homogeneous...Ch. 9.1 - Determine the distance to the center of gravity...Ch. 9.1 - Locate the centroid of the area.Ch. 9.1 - Locate the centroid x of the parabolic area. Prob....Ch. 9.1 - Locate the centroid of the shaded area. Prob. 9-8Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the area. Probs. 9-11/12Ch. 9.1 - Locate the centroid of the area. Probs. 9-11/12Ch. 9.1 - Locate the centroid x of the area. Probs. 9-13/14Ch. 9.1 - Locate the centroid of the area. Probs. 9-13/14Ch. 9.1 - Solve the problem by evaluating the integrals...Ch. 9.1 - Solve the problem by evaluating the integrals...Ch. 9.1 - Locate the centroid of the area. Prob. 9-17Ch. 9.1 - Locate the centroid x of the area. Probs. 9-18/19Ch. 9.1 - Locate the centroid of the area. Probs. 9-18/19Ch. 9.1 - Locate the centroid of the shaded area.Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Determine the location of its center of gravity....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the area. Probs. 9-32/33Ch. 9.1 - Locate the centroid of the area. Probs. 9-32/33Ch. 9.1 - Determine the location of its center of mass. Also...Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the circular sector.Ch. 9.1 - Determine the location r of the centroid C for the...Ch. 9.1 - The material is homogeneous. Prob. 9-39Ch. 9.1 - Locate the centroid of the paraboloid. Probs....Ch. 9.1 - Locate the centroid z of the frustum of the...Ch. 9.1 - Determine the centroid of the solid. Prob. 9-42Ch. 9.1 - Locate the centroid of the quarter-cone. Prob....Ch. 9.1 - Determine its mass and the distance z to the...Ch. 9.1 - Locate the centroid z of the volume. Prob. 9-45Ch. 9.1 - Locate the centroid of the ellipsoid of...Ch. 9.1 - Locate the center of gravity z of the solid. Prob....Ch. 9.1 - Locate the centroid of the ellipsoid of...Ch. 9.1 - Locate the centroid z of the spherical segment....Ch. 9.1 - Suggestion: Use a triangular plate element...Ch. 9.2 - Locate the centroid (x,y,z) of the wire bent in...Ch. 9.2 - Locate the centroid of the beams cross-sectional...Ch. 9.2 - Locate the centroid of the beams cross-sectional...Ch. 9.2 - Locate the centroid (x,y) of the cross-sectional...Ch. 9.2 - Locate the center of mass (x,y,z) of the...Ch. 9.2 - Determine the center of mass (x,y,z) of the...Ch. 9.2 - If the mass of the gusset plates at the joints and...Ch. 9.2 - Determine the location (x,y,z) of the centroid of...Ch. 9.2 - Determine the location (x,y) of the centroid of...Ch. 9.2 - Neglect the thickness of the material and slight...Ch. 9.2 - Neglect the thickness of the material and slight...Ch. 9.2 - Each plate has a constant width in the z direction...Ch. 9.2 - Neglect the thickness of each segment. The mass...Ch. 9.2 - Neglect the size of the corner welds at A and B...Ch. 9.2 - Prob. 59PCh. 9.2 - Locate the centroid for the beams cross-sectional...Ch. 9.2 - Determine the location of the centroid C of the...Ch. 9.2 - Locate the centroid (x,y) of the shaded area....Ch. 9.2 - Neglect the size of the corner welds at A and B...Ch. 9.2 - Locate the centroid (x,y) of the shaded area....Ch. 9.2 - Determine the location (x,y) of the centroid C of...Ch. 9.2 - The beam is symmetric with respect to the y axis....Ch. 9.2 - Assume all corners are square and neglect the size...Ch. 9.2 - Prob. 68PCh. 9.2 - If it is folded over as shown, determine the...Ch. 9.2 - Locate the center of mass z of the forked level...Ch. 9.2 - Prob. 71PCh. 9.2 - Prob. 72PCh. 9.2 - Prob. 73PCh. 9.2 - The location of the center of gravity of each...Ch. 9.2 - Locate the center of mass (x,y,z) of the...Ch. 9.2 - Determine the location (x,y,z) of its centroid....Ch. 9.2 - It the cord is cut, the part will rotate about the...Ch. 9.2 - Prob. 78PCh. 9.2 - Prob. 79PCh. 9.2 - Prob. 80PCh. 9.2 - The assembly is made from a steel hemisphere. st =...Ch. 9.2 - The assembly is made from a steel hemisphere, st =...Ch. 9.2 - Prob. 83PCh. 9.2 - Determine the distance h to which a...Ch. 9.2 - Determine the distance z to the centroid of the...Ch. 9.2 - The cylinder and the cone are made from materials...Ch. 9.2 - Major floor loadings in a shop are caused by the...Ch. 9.2 - Determine the distance x to its center of gravity...Ch. 9.2 - Determine the mass and location (x,y,z) of its...Ch. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Prob. 14FPCh. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Prob. 90PCh. 9.3 - Prob. 91PCh. 9.3 - Determine the volume of the storage tank. Probs....Ch. 9.3 - Prob. 93PCh. 9.3 - Determine the total weight of the wall if the...Ch. 9.3 - Determine its volume.Ch. 9.3 - Prob. 96PCh. 9.3 - Determine the volume of concrete needed to...Ch. 9.3 - Do not include the area of the ends in the...Ch. 9.3 - Prob. 99PCh. 9.3 - Prob. 100PCh. 9.3 - Prob. 101PCh. 9.3 - Each gallon of paint can cover 250 ft2. Probs....Ch. 9.3 - Determine the surface area and the volume of the...Ch. 9.3 - Prob. 104PCh. 9.3 - Determine how many joules (J) are radiated within...Ch. 9.3 - Prob. 106PCh. 9.3 - Prob. 107PCh. 9.3 - Prob. 108PCh. 9.3 - Prob. 109PCh. 9.3 - Prob. 110PCh. 9.3 - Prob. 111PCh. 9.3 - Prob. 112PCh. 9.3 - Prob. 113PCh. 9.3 - Prob. 114PCh. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-17Ch. 9.5 - The specific weight of water is = 62.4 lb/ft3.Ch. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-19Ch. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-20Ch. 9.5 - The specific weight of water is = 62.4 lb/ft3....Ch. 9.5 - Determine the magnitude of the resultant force and...Ch. 9.5 - Determine the magnitude of the resultant force and...Ch. 9.5 - The load over the plate varies linearly along the...Ch. 9.5 - The load is defined by the expression p = p0 sin...Ch. 9.5 - If this pressure loading acts uniformly along the...Ch. 9.5 - For the condition of high tide shown, determine...Ch. 9.5 - Determine the resultant force the water exerts on...Ch. 9.5 - If the density of concrete is c = 2.5 Mg/m3, and...Ch. 9.5 - Determine this factor if the concrete has a...Ch. 9.5 - Determine the magnitude of the resultant...Ch. 9.5 - If it is filled to the top, determine the...Ch. 9.5 - Prob. 126PCh. 9.5 - Determine the reactions at these supports due to...Ch. 9.5 - The tank is filled with a liquid that has a...Ch. 9.5 - The gate has a width of 1.5 m. w = 1.0 Mg/m3....Ch. 9.5 - Prob. 130PCh. 9.5 - Locate the centroid x of the area.Ch. 9.5 - Locate the centroid of the area.Ch. 9.5 - Prob. 3RPCh. 9.5 - Locate the centroid of the rod. Prob. R9-4Ch. 9.5 - Prob. 5RPCh. 9.5 - Prob. 6RPCh. 9.5 - Determine the volume of material required to make...Ch. 9.5 - Prob. 8RPCh. 9.5 - Determine the horizontal and vertical components...Ch. 9.5 - Determine the magnitude of the resultant...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Figure below shows a link mechanism in which the link OA rotates uniformly in an anticlockwise direction at 10 rad/s. the lengths of the various links are OA=75 mm, OB-150 mm, BC=150 mm, CD-300 mm. Determine for the position shown, the sliding velocity of D. A 45 B Space Diagram o NTS (Not-to-Scale) C Darrow_forwardmotion is as follows; 1- Dwell 45°. Plot the displacement diagram for a cam with flat follower of width 14 mm. The required 2- Rising 60 mm in 90° with Simple Harmonic Motion. 3- Dwell 90°. 4- Falling 60 mm for 90° with Simple Harmonic Motion. 5- Dwell 45°. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm.arrow_forwardAn ideal gas, occupying a volume of 0.02 m3 , has a temperature of 25 0C and is at 1.2 bar. The gas is compressed reversibly and adiabatically to a final pressure of 8 bar. Assuming the gas has an adiabatic index of γ = 1.4, calculate (a) the final temperature, (b) the final volume, (c) the work performed during the compression and (d) the heat transferred.arrow_forward
- attached is a past paper question in which we werent given the solution. a solution with clear steps and justification would be massively appreciated thankyou.arrow_forwardin this scenario, when it comes to matrix iterations it states this system is assumed out of phase. why is this?arrow_forwardQ1. A curved beam of a circular cross section of diameter "d" is fixed at one end and subjected to a concentrated load P at the free end (Fig. 1). Calculate stresses at points A and C. Given: P = 800 N, d = 30 mm, a 25 mm, and b = 15 mm. Fig.1 P b B (10 Marks)arrow_forward
- You are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (p = 0.001 kg m-1 s-1) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be y = +h I 2h = 1 cm x1 y = -h u(y) 1 dP 2μ dx -y² + Ay + B moving plate stationary plate U 2 I2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page.arrow_forwardQuestion 1 You are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (µ = 0.001 kg m¯¹ s¯¹) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be 1 dP u(y) = 2μ dx -y² + Ay + B y= +h Ꮖ 2h=1 cm 1 x1 y = −h moving plate stationary plate 2 X2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page. (a) By considering the appropriate boundary conditions, show that the constants take the following forms: U U 1 dP A =…arrow_forwardQuestion 2 You are an engineer working in the propulsion team for a supersonic civil transport aircraft driven by a turbojet engine, where you have oversight of the design for the engine intake and the exhaust nozzle, indicated in Figure Q2a. The turbojet engine can operate when provided with air flow in the Mach number range, 0.60 to 0.80. You are asked to analyse a condition where the aircraft is flying at 472 m/s at an altitude of 14,000 m. For all parts of the question, you can assume that the flow path of air through the engine has a circular cross section. (a) ← intake normal shock 472 m/s A B (b) 50 m/s H 472 m/s B engine altitude: 14,000 m exhaust nozzle E F exit to atmosphere diameter: DE = 0.30 m E F diameter: DF = 0.66 m Figure Q2: Propulsion system for a supersonic aircraft. a) When the aircraft is at an altitude of 14,000 m, use the International Standard Atmosphere in the Module Data Book to state the local air pressure and tempera- ture. Thus show that the aircraft speed…arrow_forward
- يكا - put 96** I need a detailed drawing with explanation or in wake, and the top edge of im below the free surface of the water. Determine the hydrothed if hydrostatic on the Plot the displacement diagram for a cam with roller follower of diameter 10 mm. The required motion is as follows; 1- Rising 60 mm in 135° with uniform acceleration and retardation motion. 2- Dwell 90° 3- Falling 60 mm for 135° with Uniform acceleration-retardation motion. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm. =--20125 7357 750 X 2.01arrow_forwardYou are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (µ = 0.001 kg m¯¹ s¯¹) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be U y = +h У 2h = 1 cm 1 x1 y=-h u(y) = 1 dP 2μ dx -y² + Ay + B moving plate - U stationary plate 2 I2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page. (a) By considering the appropriate boundary conditions, show that the constants take the following forms: A = U 2h U 1 dP…arrow_forwardQuestion 2 You are an engineer working in the propulsion team for a supersonic civil transport aircraft driven by a turbojet engine, where you have oversight of the design for the engine intake and the exhaust nozzle, indicated in Figure Q2a. The turbojet engine can operate when provided with air flow in the Mach number range, 0.60 to 0.80. You are asked to analyse a condition where the aircraft is flying at 472 m/s at an altitude of 14,000 m. For all parts of the question, you can assume that the flow path of air through the engine has a circular cross section. (a) normal shock 472 m/s A B (b) intake engine altitude: 14,000 m D exhaust nozzle→ exit to atmosphere 472 m/s 50 m/s B diameter: DE = 0.30 m EX diameter: DF = 0.66 m Figure Q2: Propulsion system for a supersonic aircraft. F a) When the aircraft is at an altitude of 14,000 m, use the International Standard Atmosphere in the Module Data Book to state the local air pressure and tempera- ture. Thus show that the aircraft speed of…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
moment of inertia; Author: NCERT OFFICIAL;https://www.youtube.com/watch?v=A4KhJYrt4-s;License: Standard YouTube License, CC-BY