
Consider a Mach 4 airflow at a pressure of 1 atm. We wish to slow this flow to subsonic speed through a system of shock waves with as small a loss in total pressure as possible. Compare the loss in total pressure for the following three shock systems:
a. A single normal shock wave
b. An oblique shock with a deflection angle of
c. An oblique shock with a deflection angle of
From the results of (a), (b), and (c), what can you induce about the efficiency of the various shock systems?
(a)
The comparison in total pressure loss for the single normal shock wave.
Answer to Problem 9.8P
The loss in pressure is
Explanation of Solution
Given:
The Mach number is
The pressure is
Formula used:
The expression for
The expression for
The expression for loss in pressure is given as,
Calculation:
The pressure
The pressure
The loss in pressure can be calculated as,
Conclusion:
Therefore, the loss in pressure is
(b)
The comparison in pressure for an oblique shock with a deflection angle of
Answer to Problem 9.8P
The loss in pressure is
Explanation of Solution
Given:
The Mach number is
The pressure is
The deflection angle of oblique shock wave is
Formula used:
The expression for
The expression for
The expression for
The expression for loss in pressure is given as,
Calculation:
From
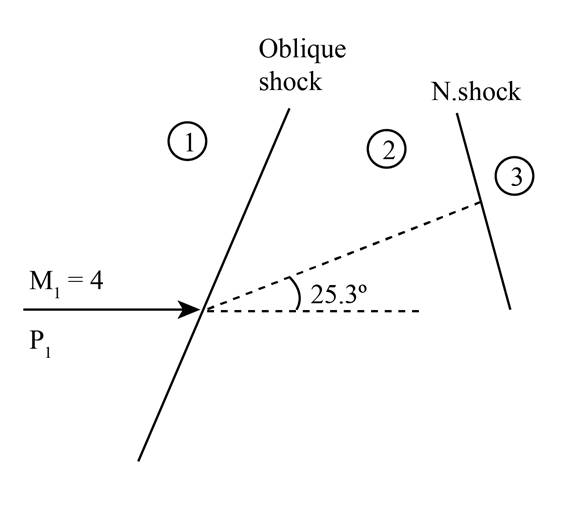
Figure (1)
The Mach number
The pressure ratio for Mach number
From appendix B
The Mach number
The pressure ratio for Mach number
The pressure
The pressure loss can be calculated as,
Conclusion:
Therefore, the loss in pressure is
(c)
The comparison in pressure for the an oblique shock with a deflection angle of
Answer to Problem 9.8P
The loss in pressure is
Explanation of Solution
Given:
The Mach number is
The pressure is
The deflection angle of second oblique shock wave is
Formula used:
The expression for the Mach number
The expression for Mach number
The expression for the pressure
The expression for loss in pressure is given as,
Calculation:
From
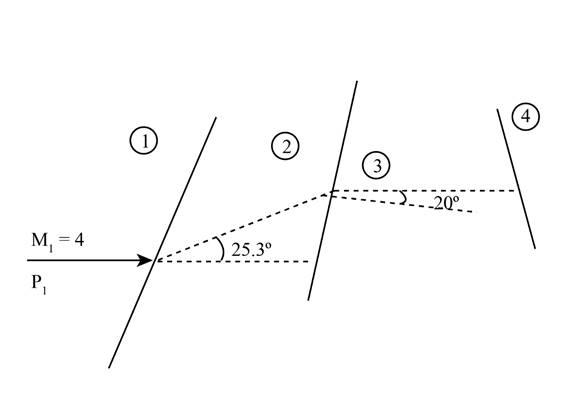
Figure (2)
The Mach number
The pressure ratio for Mach number from appendix B is given as,
Refer to appendix B
The Mach number
The pressure ratio for Mach number
The pressure
The pressure loss can be calculated as,
From a, b and c it is clear that the most efficient way to decrease supersonic flow to subsonic flow is through a combination of supersonic diffuser and then normal shock wave at the end.
Conclusion:
Therefore, the loss in pressure is
Want to see more full solutions like this?
Chapter 9 Solutions
Fundamentals of Aerodynamics
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD. The roof truss shown carries roof loads, where P = 10 kN. The truss is consisting of circular arcs top andbottom chords with radii R + h and R, respectively.Given: h = 1.2 m, R = 10 m, s = 2 m.Allowable member stresses:Tension = 250 MPaCompression = 180 MPa1. If member KL has square section, determine the minimum dimension (mm).2. If member KL has circular section, determine the minimum diameter (mm).3. If member GH has circular section, determine the minimum diameter (mm).ANSWERS: (1) 31.73 mm; (2) 35.81 mm; (3) 18.49 mmarrow_forwardPROBLEM 3.23 3.23 Under normal operating condi- tions a motor exerts a torque of magnitude TF at F. The shafts are made of a steel for which the allowable shearing stress is 82 MPa and have diameters of dCDE=24 mm and dFGH = 20 mm. Knowing that rp = 165 mm and rg114 mm, deter- mine the largest torque TF which may be exerted at F. TF F rG- rp B CH TE Earrow_forward1. (16%) (a) If a ductile material fails under pure torsion, please explain the failure mode and describe the observed plane of failure. (b) Suppose a prismatic beam is subjected to equal and opposite couples as shown in Fig. 1. Please sketch the deformation and the stress distribution of the cross section. M M Fig. 1 (c) Describe the definition of the neutral axis. (d) Describe the definition of the modular ratio.arrow_forward
- using the theorem of three moments, find all the moments, I only need concise calculations with minimal explanations. The correct answers are provided at the bottomarrow_forwardMechanics of materialsarrow_forwardusing the theorem of three moments, find all the moments, I need concise calculations onlyarrow_forward
- Can you provide steps and an explaination on how the height value to calculate the Pressure at point B is (-5-3.5) and the solution is 86.4kPa.arrow_forwardPROBLEM 3.46 The solid cylindrical rod BC of length L = 600 mm is attached to the rigid lever AB of length a = 380 mm and to the support at C. When a 500 N force P is applied at A, design specifications require that the displacement of A not exceed 25 mm when a 500 N force P is applied at A For the material indicated determine the required diameter of the rod. Aluminium: Tall = 65 MPa, G = 27 GPa. Aarrow_forwardFind the equivalent mass of the rocker arm assembly with respect to the x coordinate. k₁ mi m2 k₁arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





